5. Фазовый переход на p-V диагремме согласно уравнению Ван-дель-Ваальса. Метастабильное состояние

Метастабильное состояние (от греч. μετα «через» и лат. stabilis «устойчивый») — состояние квазиустойчивого равновесияфизической системы, в котором система может находиться длительное время.

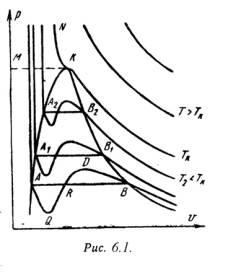
На PV – диаграмме (рис.6.1) показаны изотермы построенные по уравнению Ван-дер-Ваальса. Из кривых видно, что при сравнительно низких температурах имеются волнообразные участки. Чем выше температура, тем короче эти части кривых. Эти волнообразные кривые указывают на непрерывный переход от жидкого состояния в парообразное при данной температуре. Точка А соответствует состояниижидкости, точка В относится парообразному состоянии вещества.

В действительности переход из жидкого состояния в парообразное всегда происходит через двухфазное состояние вещества. При этом при данной температуре процесс перехода происходит также и при постоянном давлении. Этот действительный переход из жидкого состояния в парообразное изображается прямой линией АВ. Практически для особо чистых веществ возможно осуществление участков волнообразной кривой AQ и DB. В первом случае имеют место неустойчивые состояния перегретой жидкости, а во втором – переохлажденного пара. При определенной температуре изотерма уравнения Ван-дер-Ваальса не будет иметь волнообразного участка (точка К). Этутемпературу называют критической. Если соединить точки А₁, А₂, А₃ … и В₁, В₂, В₃ ... получим кривую похожую на параболу. Кривая АК называется нижней пограничной кривой и соответствует в состоянии кипения жидкости. Кривая КВ называется верхней пограничной кривой и соответствует состояния сухого насыщенного пара. Таким образом, для реального вещества PV – диаграмму можно разбить на 3 области: 1 - область жидкого состояния, расположена левее нижней пограничной кривой; 2 - область двухфазных состояний (влажный пар), расположена между нижней и верхней пограничной кривой); 3 – область перегретого пара, расположена правее верхней пограничной кривой и выше критической точки. Условно область жидкостиограничивают сверху линией КМ – критическая изобара. Критическую температуру Д.И.Менделеев называл абсолютной температурой кипения, при которой поверхностное натяжение вжидкости становится равным нулю, т.е. исчезает различие между жидкостью и парообразным состоянием вещества (насыщеннымпаром).  Связь между критическими параметрами и постоянными уравнения Ван-дер-Ваальса:

Т_к = 8·а/(27·R·b) ; P_к = a/(27·b²) ; (6.4) а = (27· R² ·Т²_к)/(64 ·P_к) ; b = (27· R ·Т_к)/(8 ·P_к). (6.5)

Уравнение Ван-дер-Ваальса при больших плотностях газа дает значительные ошибки. Кроме этого экспериментальным путем доказана, что коэффициенты а, b зависят от температуры и давления, причем эта зависимость очень сложная. М.П.Вукалович и И.И.Новиков в 1939 г. предложили новое универсальное уравнение состояния реальных газов с учетом ассоциации идиссоциации их молекул, который имеет следующий вид:

(P + a/²)·( – b) = R·T (1 – С/(  ·Т^(3+2m)/2), (6.6)

Где a, b – постоянные уравнения Ван-дер-Ваальса; С, m – постоянные, определяемые на основании опытных данных.

6.

Фа́зовая диагра́мма (диаграмма состоя́ния) — графическое отображение равновесного состояния бесконечной физико-химической системы при условиях, отвечающих координатам рассматриваемой точки на диаграмме (носит название фигуративной точки).

Обычными координатами для построения фазовой диаграммы являются термодинамические параметры — температура и давление — и состав системы (в мольных или массовых процентах).

В общем случае количество координат превышает число компонентов системы на единицу (диаграмма однокомпонентной системы двумерна, двухкомпонентной — трёхмерна и т. п.) Для конденсированных систем зачастую не учитывают изменение фазовых равновесий за счёт давления, в этом случае число измерений диаграммы равно числу компонентов (диаграмма конденсированной двухкомпонентной системы двумерна, трёхкомпонентной — трёхмерна и т. п.) Сложные фазовые диаграммы в печатных изданиях изображают в виде сечений или проекций.

Согласно правилу фаз, на двумерной диаграмме однофазная область описывается полем, двухфазная — линией (на p-T диаграммах) или набором параллельных линийконод, для которых фиксированы составы равновесных фаз (на диаграммах с участием состава), трёхфазная — точкой (на p-T диаграммах) или горизонталью (на T-x или p-x диаграммах).

На фазовых диаграммах однокомпонентных систем поля, по правилу фаз, соответствуют однофазным состояниям, линии, разграничивающие их — двухфазным, точки пересечения линий — трёхфазным (эти точки называют тройными точками).

Двухфазные линии, как правило, либо соединяют две тройные точки, либо тройную точку с точкой на оси ординат, отвечающую нулевому давлению. Исключение составляет линия жидкость-газ, заканчивающаяся в критической точке. При температурах выше критической различие между жидкостью и паром исчезает.

Тройна́я то́чка — точка на фазовой диаграмме, где сходятся три линии фазовых переходов. Тройная точка — это одна из характеристик вещества. Обычно тройная точка определяется значением температуры и давления, при котором вещество может равновесно находиться в трёх (отсюда и название) агрегатных состояниях: твёрдом, жидком и газообразном. В этой точке сходятся линии плавления, кипения и возгонки.

В более общем случае могут рассматриваться и другие фазы вещества, не соответствующие различным агрегатным состояниям. На достаточно богатых фазовых диаграммах может быть несколько тройных точек. Вещество в тройной точке в состоянии термодинамического равновесия может частично находиться во всех трёх фазах. На многомерных фазовых диаграммах (то есть если кроме температуры и давления присутствуют иные интенсивные величины) могут существовать четверные и т. д. точки.

Критическая точка — сочетание значений температуры   и давления   (или, что эквивалентно, молярного объёма  ), при которых исчезает различие в свойствах жидкой и газообразной фаз вещества.