
- •Кинематика Математические операции над векторными величинами
- •2. Основные кинематические понятия и характеристики.
- •3. Типы прямолинейного движения:
- •Кинематические характеристики вращательного движения и их связь с характеристиками поступательного движения.
- •Динамика материальной точки. Законы Ньютона
- •Закон Всемирного тяготения
- •Динамика вращательного движения твердого тела
- •Закон Максвелла о распределении молекул по скоростям
- •Применение закона термодинамики и изопроцессам. Адиабатный процесс.
- •Электростатическое поле
- •Постоянный электрический ток.
- •Магнитное поле, его свойства и характеристики.
Динамика вращательного движения твердого тела
Момент инерции материальной точки относительно неподвижной оси вращения равен произведению её массы на квадрат расстояния до рассматриваемой оси вращения
![]() .
.
Момент инерции тела равен сумме моментов инерции всех его точек:
![]() .
.
Момент инерции обруча (толщиной стенок пренебрегаем) или полого цилиндра:

![]() .
.
Момент инерции диска или сплошного цилиндра радиуса R:
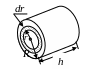
![]()
,
Момент инерции шара

![]() .
.
Момент инерции стержня

![]() .
.
Теорема Штейнера: момент инерции тела относительно произвольной оси равен моменту инерции J0 относительно оси, параллельной данной и проходящей через центр масс тела, сложенному с произведением массы тела на квадрат расстояния между осями.
![]()
 ,
,
где d расстояние от центра масс О до оси вращения (рис.).
М оментом
силы
относительно точки О называется векторная
величина, равная векторному произведению
радиус-вектора
оментом
силы
относительно точки О называется векторная
величина, равная векторному произведению
радиус-вектора
![]() проведенного из точки О в точку приложения
силы, на вектор силы:
проведенного из точки О в точку приложения
силы, на вектор силы:
![]() .
.
Модуль момента силы численно равен произведению силы на плечо:
![]() ,
,
где
![]() - плечо силы относительно точки О,
- угол между направлениями
- плечо силы относительно точки О,
- угол между направлениями
![]() и
и
![]() ,
,
![]() .
.
Плечо - кратчайшее расстояние от центра вращения до линии действия силы.
Моментом
силы
относительно неподвижной оси Z
называется проекция вектора
![]() на эту ось (проходящую через точку О):
на эту ось (проходящую через точку О):
![]() .
.
Основное уравнение динамики вращательного движения
![]() ,
,
![]() ,
,
т.е. угловое ускорение тела прямо пропорционально моменту действующих на него внешних сил и обратно пропорционально его моменту инерции. Уравнение (1) представляет собой уравнение динамики вращательного движения твердого тела относительно неподвижной оси, или второй закон Ньютона для вращательного движения.
Момент
импульса
материальной точки
![]() относительно неподвижной точки О равен
векторному произведению радиуса-вектора
относительно неподвижной точки О равен
векторному произведению радиуса-вектора
![]() ,
проведенного из полюса О к данной
материальной точке, на ее импульс
,
проведенного из полюса О к данной
материальной точке, на ее импульс
![]() :
:
![]() .
.
Моментом
импульса
относительно неподвижной оси называется
проекция вектора
![]() на эту ось.
на эту ось.
Момент импульса твердого тела относительно неподвижной оси равен сумме моментов импульсов всех его точек относительно этой оси:
![]() .
.
Продифференцируем это уравнение по времени:
![]() т.е.
т.е.
![]() .
.
Это уравнение - ещё одна форма основного уравнения динамики вращательного движения твердого тела относительно неподвижной оси.
Закон
сохранения момента импульса: момент
импульса системы относительно какой-либо
неподвижной оси остается постоянным,
если момент внешних сил относительно
этой оси равен нулю, т.е. если для какой-то
оси
![]()
![]() .
.
Работа
при вращательном движении
![]()
Кинетическая
энергия
вращающегося тела
![]() .
.
Если
тело катится, то
![]() .
.
Молекулярно-кинетическая теория (МКТ)
Идеальный газ - это газ, молекулы которого можно рассматривать как материальные точки, а их взаимодействие носит характер абсолютно упругого удара. (при низком р и высокой Т реальные газы приближаются к идеальным).
Т= tС+ 273, t.
Уравнение
состояния идеального газа:
![]() .
.
Уравнение
Менделеева-Клапейрона:
![]() .
.
И зопроцессы
зопроцессы
![]()
Т= const – изотермический процесс,
![]() или
или
![]()
р
 =
const
– изобарный процесс,
=
const
– изобарный процесс,
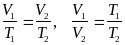 или
или
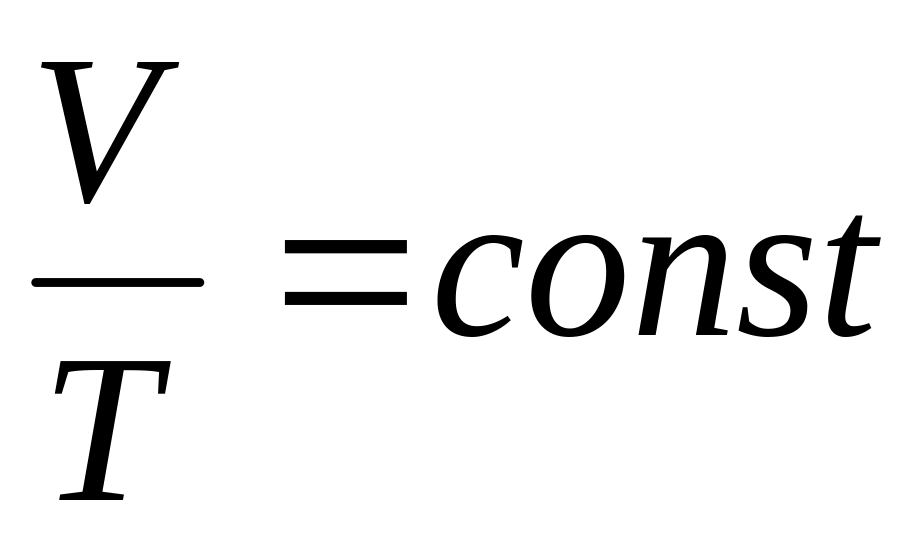
V
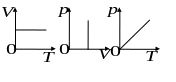 =const
– изохорный
процесс,
=const
– изохорный
процесс,
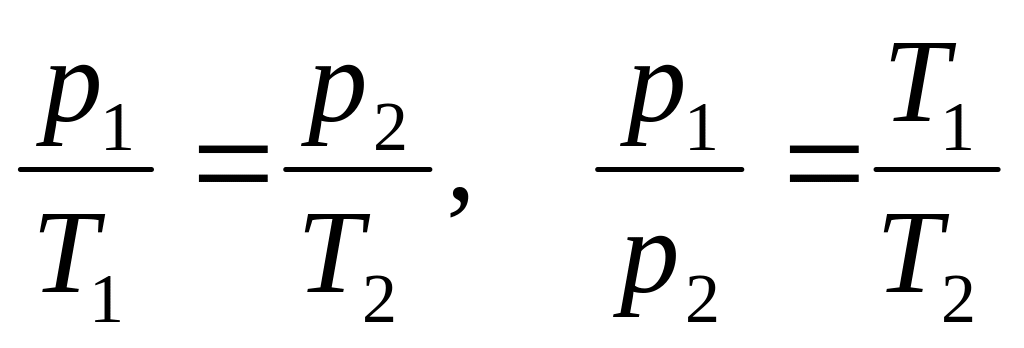 или
или
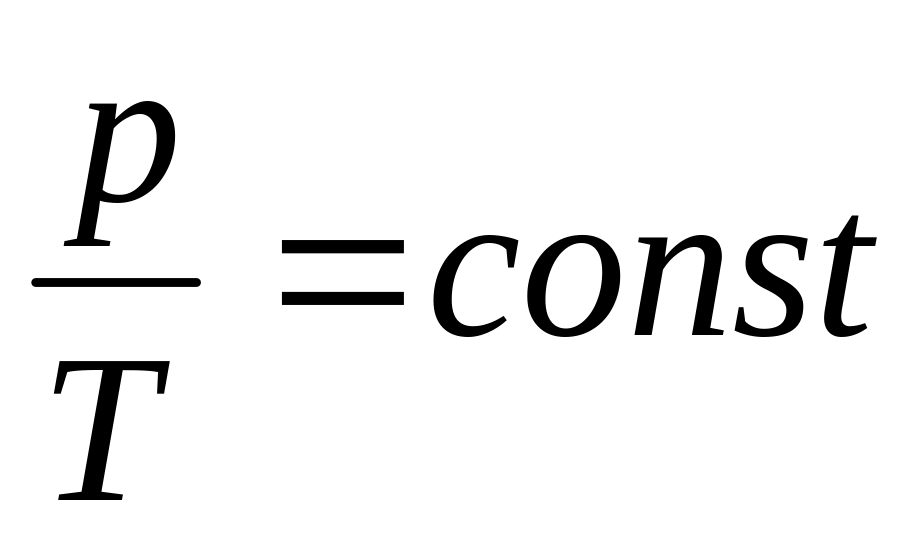
Основное
уравнение МКТ
![]() ,
или
,
или
![]() где
где
 -средняя
квадратичная скорость,
-средняя
квадратичная скорость,
![]() ,
,
![]() -
средняя кинетическая энергия
поступательного движения одной молекулы.
-
средняя кинетическая энергия
поступательного движения одной молекулы.
Поскольку
![]()
![]()
![]() ,
,
![]() .
.
