Кинематика Математические операции над векторными величинами
1.Сложение векторов
а)
и
сонаправлены:
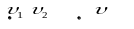
б) и направлены противоположно:
в)
,
используется правило параллелограмма:
.
2
.Вычитание
векторов
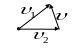
Производная вектора
, 
– знак
изменения,
d – знак бесконечно малого изменения.
Понятие интеграла.
.
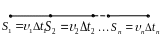Если
n
– велико, а
- мало, то 
.
При
.
Примеры
интегралов:
, 
,
.
2. Основные кинематические понятия и характеристики.
Механическое движение - это изменение положения тел или их частей в пространстве с течением времени.
Материальной точкой называют тело, размерами и формой которого можно пренебречь в условиях данной задачи.
Абсолютно твердым телом называют тело, деформациями которого можно пренебречь в условиях данной задачи.
Поступательным назвали такое движение, при котором любая прямая, проведенная в теле, остается параллельной самой себе (рис.1).
характеристики быстроты изменения скорости вводится понятие ускорения.
Средним
ускорением
называют отношение изменения скорости
к интервалу времени t,
за которое это изменение произошло:
,
.
Направление
вектора
совпадает
с направлением вектора
.
Мгновенное ускорение - векторная величина, равная первой производной скорости по времени:
;
.
3. Типы прямолинейного движения:
а) переменное движение - движение, при котором изменяются как скорость, так и ускорение,
б) равнопеременное движение – движение с постоянным ускорением,
,
- равноускоренное,
- равнозамедленное,
;
,
,
;
;
в) равномерное движение – движение с постоянной скоростью,
,
.
Тангенциальное
ускорение
характеризует изменение скорости по
величине Его модуль равен
.
Нормальное ускорение характеризует изменение скорости по направлению,
направлено
вдоль радиуса R
к центру окружности:
.
Полное ускорение материальной точки при криволинейном движении характеризует быстроту изменения скорости как по величине, так и по направлению
, 
.
Кинематические характеристики вращательного движения и их связь с характеристиками поступательного движения.
Поворот тела на некоторый угол можно задать в виде отрезка, длина которого равна , а направление совпадает с осью, вокруг которой производится поворот. Направление поворота и изображающего его отрезка связано правилом правого винта.
В
математике показывается, что очень
малые повороты можно рассматривать как
векторы, обозначаемые символами
или
.
Направление вектора поворота связывается
с направлением вращения тела;
- вектор
элементарного поворота тела,
является
псевдовектором, так как не имеет точки
приложения.
П
ри
вращательном движении твердого тела
каждая точка движется по окружности,
центр которой лежит на общей оси вращения.
При этом радиус-вектор R,
направленный от оси вращения к точке,
поворачивается за время t
на некоторый угол .
Для характеристики вращательного
движения вводится угловая скорость и
угловое ускорение.
Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:
Направление угловой скорости задается правилом правого винта: вектор угловой скорости сонаправлен с , то есть с поступательным движением винта, головка которого вращается в направлении движения точки по окружности.
Линейная скорость точки связана с угловой скоростью:
.
В
векторной форме
.
Если в процессе вращения угловая скорость изменяется, то возникает угловое ускорение.
Угловое ускорение – векторная величина, равная первой производной угловой скорости по времени:
Вектор
угловой скорости сонаправлен с вектором
элементарного изменения угловой скорости
,
происшедшего за время dt.
При
ускоренном движении вектор
сонаправлен
,
при замедленном – противонаправлен.
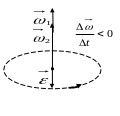
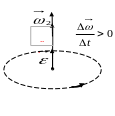
Связь между линейными и угловыми величинами:
Типы вращательного движения.
а)
переменное
–
вращательное движение, при котором
изменяются
и
:
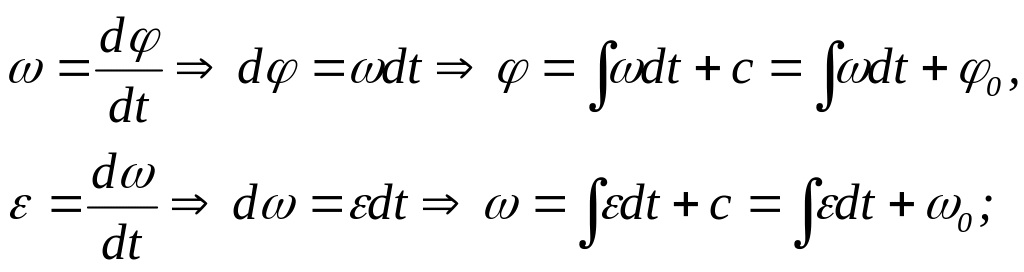
б) равнопеременное – вращательное движение с постоянным угловым ускорением:
.
в) равномерное – вращательное движение с постоянной угловой скоростью:
.
Равномерное
вращательное движение можно характеризовать
периодом
и частотой вращения
.
Период – это время, за которое тело совершает один полный оборот.
,
[T]
= c.
Частота вращения – это число оборотов, совершаемых за единицу времени.
,
[]
= c-1.
За
один оборот: 
,
, 
.