Есептеу нәтижесі 7-ші кестеде

7-ші кесте

li	ki	nпрi	Q(l)
20-30	1.025	1.025	0.025
30-40	1.025	10.250	0.250
40-50	1.139	26.296	0.641
50-60	2.100	32.596	0.795
60-70	2.800	38.196	0.931

Q(l) алынған мәндір 1 аралығынан тәуелді ықтималдық қағазға енгіземіз, сенімділіктің таралым заңын анықтаймыз және кесте бойынша таралымның заң параметрін табамыз.

Ықтималды қағаз – бұл кездейсоқ шаманың аналитикалық өзгеріс заң формуласымен сәйкес құрылған координат торы. Осы кезде кездейсоқ шаманың сызықтық емес тәуелділігі ықтималды қағазда сызықтық болады. Ол бұйымның сенімділікке тексеру нәтижесін өңдеу кезінде қолданылады.

Жалпы жағдайда қабыл алмау ықтималды тәуелділігі бұйымның жұмыс тәртібінен сызықтық емес функциясын ұсынады, егер осы тәуелділікті тікбұрышты координат жүйесіне енгізсек. Бірақ қабыл алмау ықтималды функциясы немесе аргумент функциясын немесе екеуінің шамасын пайда бола таралым функцияның кестесін сызықтық етуге болады. Оны екі әдіспен құруға болады:

— көрсетілген өзгерістің тікелей жүргізуімен;

— көрсетілген өзгерістерге жауап беретін, сәйкес бөліктер енгізілген арнайы ықтималды қағазда.

Біздің өнекәсіпте қағаз ықтималды көрсеткішпен шығарылмағандықтан (логарифмдік, координат торымен қағаздар бар), онда оны өзімізге дайындауға болады.

Ықтималды қағазды дайындауға ыңғайлы:

— Машинаның сенімділігі туралы тәжірибелі мәліметтерге теориялық заңда анықтау үшін;

- теоретикалық заң параметрлерін графикалық әдіспен анықтау үшін;

Болінудің қалыпты заңы үшін ықтималдық шкала құру

Егер қалыпты заңға сәйкес істен шығудың ықтималдық функциясын төмендегідей белгілесек

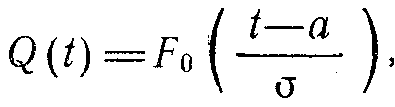
Онда квантиль формуласы келесі түрде жазылады:

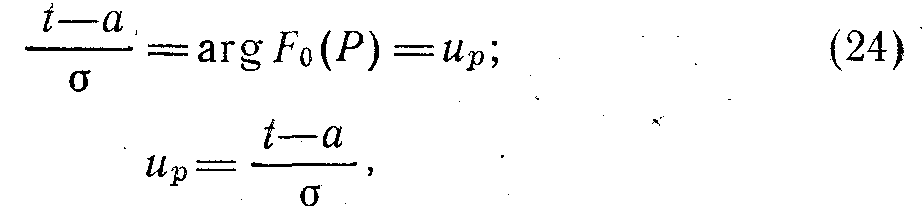
Мұндағы а және δ — математикалық күту мен орташаквадратты ауытқуына сәйкес

Квантиль — оның берілген ықтималдық мәніне сәйкес келетін функцияның аргументі.

(24) теңдеуінен u_р тәуелділігі ауыспалы l тәуелділігі – сызықтық болып табылады. Сондықтан қарапайым заң үшін ықтималды қағаз былай құрылады: t үшін біркелкі көрсеткіш абсцисса осінде, ал сәйкес келетін Q(t) шамасы ординат осінде жиналады. Ординат көрсеткіш осінде біркелкі емес болып шығады.

T өзгеріс аймағында Δt = t_max - t_{min /} айырмасымен анықталады. Егер біз графиктің еніне А мм қабылдасақ, онда абсцисса осінде t мәнін l_t = Kt қатынас комегі кезінде жинауға болады, мұндағы

Таралым функцияның ординат көрсеткіш осін құру үшін Q(t)_min = 0,001 және Q(t)_max = 0,999 қабылдайық. Сонда квантиль кестесі бойынша қарапайым заңның аз мәні Up = - 3,09, ал үлкен мәні и_р = +3,09 болады. В мм ұзындығы кезінде 1_Р масштабты фактор үшін теңдеу:

Қарапайым заңның ықтималды қағаздың торы келесі түрде құрылады. Кесте бойынша әрбір берілген ықтималды мән Q(t)=p үшін сәйкес келетін квантиль u_р мәнін табамыз. Ординат осі бойынша масштабта жиналатын u_р нүктелері арқылы түзу, абсциссаның параллельді остері жүргізіледі, ал абсцисса осі бойынша біркелкі көрсеткіш t торы түсіреді.

[16] кестеде берілген ықтималды мәндер үшін қарапайым заңның квантиль мәндері келтірілген.

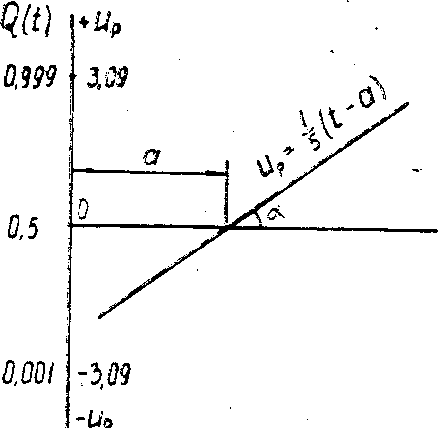
10-шы сурет. Қалыпты заң үшін ықтималдық шкала құру принципі

10. суретте кесте бойынша қарапайым заңның параметрлерін анықтауы көрсетілген.

Кестеден

Осыдан

Графиктен таралым параметрлерін анықтау кезінде масштабты факторды ескеру қажет екенін белгілейік.

Мысал. Автомобильдің фрикционды пышақты тежеуіш негіздердің бастырмаларын тойтармаға дейін тозуға жабдықтаулы сынақтары жүргізілді. Сынақтардың нәтижесі 8 кестеде келтірілген. Барлығы N_o=2184 бастырмасы жазылған.

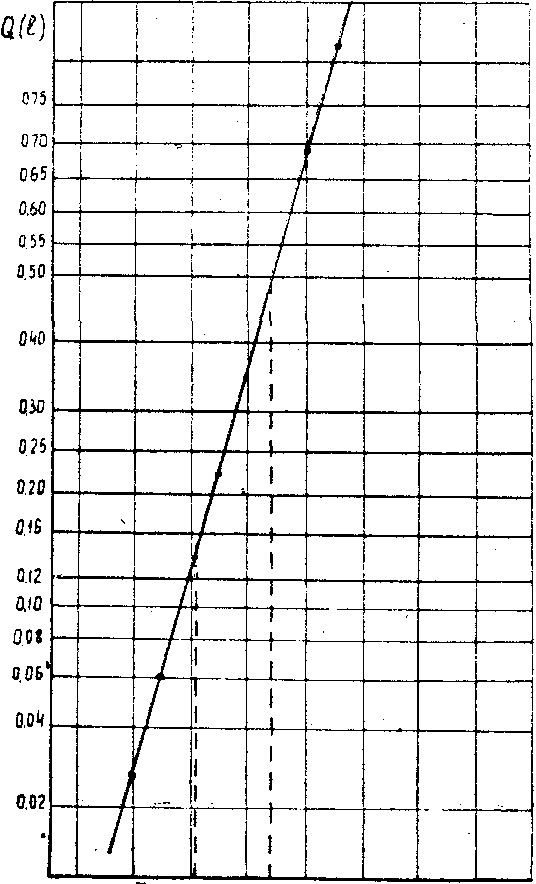
11-ші сурет. Қалыпты ықтималдық қағаз бойынша автомобиль тежеуіштерінің тозуға байланысты істен шығуларының ықтималдығы

8-ші кесте

Жүрген жол,мың.км	li-ге сәйкес істен шыққан бөлшектер саны	li жүрісіне сәйкес істен шығу тәжрибенің ықтималдылығы
li	nl	Q(ti)=
30	56	0.026
40	134	0.061
50	274	0.125
60	492	0.225
70	788	0.361
80	1144	0.524
90	1460	0.668
100	1770	0.810
110	1956	0.896
120	2080	0.952
130	2140	0.980
140	2166	0.920
150	2184	1.000

Тозылғандарды қабыл алмау көбінесе қарапайым заңмен сипатталады. Біздің жағдайда бұл таралым заңы орынға ие деп болжаймыз.

Нүкте координаталарымен l_i Q(l_i) қарапайым таралым заңының ықтималды торына түсіреді және олар арқылы түзу жүргіземіз (сурет 11). Өйткені ықтималды қабыл алмаудың тәжірибелі нүктелері автомобильдің аралығынан тәуелді қарапайым заңның ықтималды қағазында тік сызыққа орналасқан, немесе тежеуіштің бас тартуы тозу бастырмаларынан қарапайым заңға бағынады.

Q(l) = 0,5 кезінде орташа қорды анықтаймыз. 11 суретте T₀ ≈ 79 мың км екені көрсетілген. Орташаквадратты ауытқу

(мұнда Q(l) =0,159 бас тарту ықтималдығы кезінде l' аралығы бар). Вариация коэффициенті

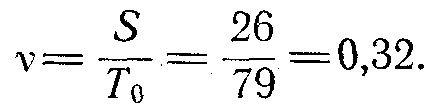
Экспоненциалды заң үшін ықтималды шкала құру

Таралымның Q(t) - l - е^-λм экспоненциалды заң кезінде ықтималдықтың қабыл алмау теңдігін логарифмдей отырып, мынаны аламыз:

(25) формуладан 1n [1—Q(t)] тәуелділігі t тәуелділігінен – сызықтық болады. Сондықтан абсцисса осі бойынша t үшін біркелкі көрсеткіш, ал тік осінде ln [1—Q(t)] мәні қойылады және Q(t) жазылады. Тік осінде көрсеткіштің торы біркелкі емес болады.