7 Сурет. Қалыпты логарифмдік заң жағдайындағы машиналар сенімділігінің сипаттамасы:

- алдыңғы доңғалақ подшипнигі;

- 20 торапта резбалық қосылулардың босауының мерзімділігі;

- стендтік сынау кезінде бөлшектердің қажудан бұзылуы.

Қалыпты логарифмдік заң жағдайындағы сенімділіктің негізгі сипаттамаларының графигі 7 суретте бейнеленген.

Вейбуллдық тарату – бұл теріс емес мәндерді ғана қабылдайтын t кездейсоқ шамасының үздіксіз таралу заңы.

Мұндай таралу үшін тоқтаусыз жұмыс істеу мүмкіндігі былай беріледі:

істен шығу мүмкіндігі –

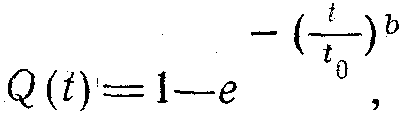
істен шығу жиілігі (тығыздықта таралу) –

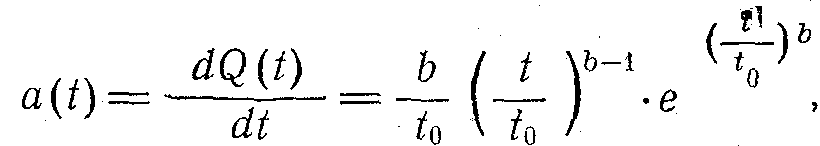
істен шығу қарқындылығы –

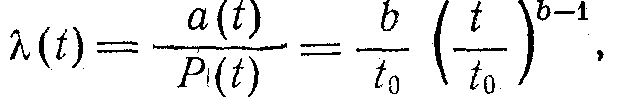
математикалық нәтижесі –

орта квадраттық ауытқуы -

Мұндағы

Г(р) – функция гаммасы кестеден алынады;

t0 b b0- Вейбуллдың тарату параметрі

Егер де бізге машиналардың істен шығуы Вейбуллдың тарату заңына бағынуы мәлім болған болса, онда мұндай таратудың параметрін вариациялау коэффициенті арқылы шамамен анықтауға болады. Бұл үшін тәжірибелі деректерден вариациялау коэффициентін табу керек, содан соң барып Вейбуллдық тарату кестесінің тәуелді коэффициенттері бойынша вариациялау коэффициенттен b, t₀ табамыз

бұл жердегі - істен шығуға арналған жұмыс;

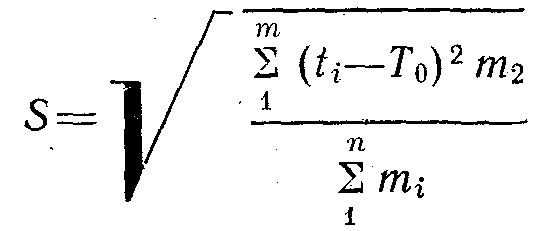- таңдаулы орташа квадраттық ауытқуы;

Р(t), а (t) функцияларының есептерін белгілі b, t₀ параметрлермен жеңілдету [16] кестеде берілген.

Үлгі. Саны 273 тұратын 6СТ-54М аккумуляторлық батареялар сынаққа алынды, ол жаппай салмағы пластиналардан шашылғанға шейін жалғасты. Сынау нәтижелері бойынша есептелді:

• T₀=164 мың км орташа ресурс;

• S = 50,7 мың км орташа квадраттық ауытқуы;

• вариациялау коэффициенті

Автомобильдің / = 90 мың км жүруі үшін сенімділік параметрін анықтау үшін аккумуляторлық батареялардың қатардан шығуы Вейбуллдың тарату заңына байланысты екені бізге белгілі болуы керек.

Шешім. [16] кестеден v = 0,31 вариациялау коэффициенті бойынша табамыз:

Параметрін анықтаймыз

қатысы бойынша Р(1) = 0,9154 істен шығу жұмысының мүмкіндігін анықтаймыз.

Істен шығу мүмкіндігі мынаған тең:

істен шығу жиілігі –

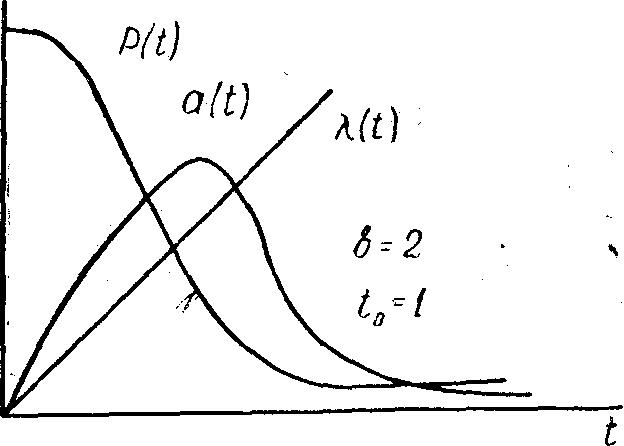
8 сурет. Вейбуллдық таралу заңы жағдайындағы машиналардың сенімділік сипаттамасы

істен шығу қарқындылығы –

Вейбуллдық таралу b = 1 көрсеткіші бойынша экспоненционалдық заңға ауысады, ал b = 3,25 заңы болғанда жақын тұрған қалыптылыққа ауысады. Вейбуллдық тарату заңы материалдың тозуы мен қажалу әрекеттері бірдей болған уақытта істен шығу көрінісі жиі болады.

Вейбуллдық тарату заңы автомобильдердің көптеген тораптары мен бөлшектерінің істен шығуын сипаттап отырады:

• шайқалу подшипнигінің істен шығуы;

• рульдік жетектердің шарнирлерінің, кардандық берудің істен шығуы;

• жартылай остердің бұзылуы;

8 суретте Вейбуллдық таралу кезіндегі сенімділік кестесі бейнеленген.

Пуассондық тарату заңы қызмет көрсету станциясына келіп жеткен автомобильдердің ағыны, қалалық көліктің аялдамаларына келетін жолаушылардың ағыны, сатып алушылар ағыны мен абоненттерді АТС т.б. тасу сияқты жаппай қызмет көрсету жүйесіндегі құбылыстардың бүтіндей бірқатарына сандық сипаттама беру үшін қолданылады. Бұл заң кездейсоқ шамалардың мүмкіндігін таратуды яғни m = 0, 1,2,3,4 және т.б. тек бүтін сандық мәндерді қабылдай алатын, берілген уақыт үзілісінде пайда болатын жағдайлардың қатарын білдіреді.

m = 0, 1,2,3.... берілген уақыт үзілісінде пайда болатын жағдайлардың қатарының мүмкіндігі Пуассондық заңында мына формуламен беріледі:

мұндағы Р(m, а) – берілген уақыт үзілісінде қарастырылған кейбір t кейбір жағдайлары бір m тең;

m – қарастырылуға берілген уақыт үзілісі ішінде оқиғалардың пайда болу қатарын білдіретін кездейсоқ шама;

t – кейбір оқиғалардың зерттелу ағымына берілетін уақыто үзілісі;

λ- уақыт бірлігіндегі оқиғалардың тығыздығы мен қарқындылығы;

а = λ t – қарастырылған уақыт үзілісіндегі оқиғалар мөлшерін математикалық нәтижесі.

Міндетті шарттарды тексеру: кез-келген құбылыстардағы барлық мүмкіндікті оқиғалардың соммасы 1-ге тең, яғни ол былай:

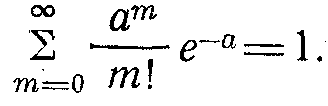
Математика курсынан бізге белгілі мынау:

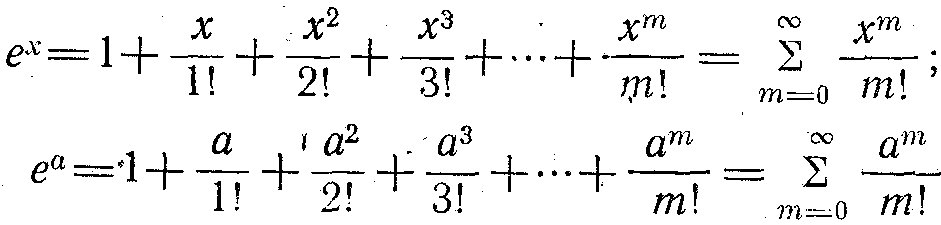
Осыдан шығады:

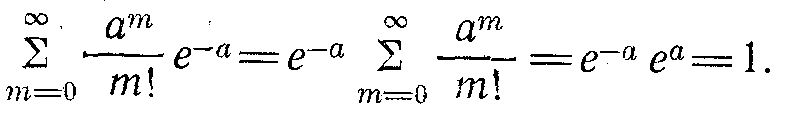
Оқиғалар мөлшеріның математикалық нәтижесі тең:

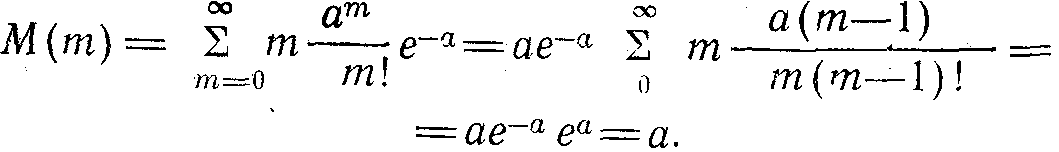
Пуассон заңы үшін дисперсия математикалық нәтижесі тең болады. Оны мынадан көруге болады:

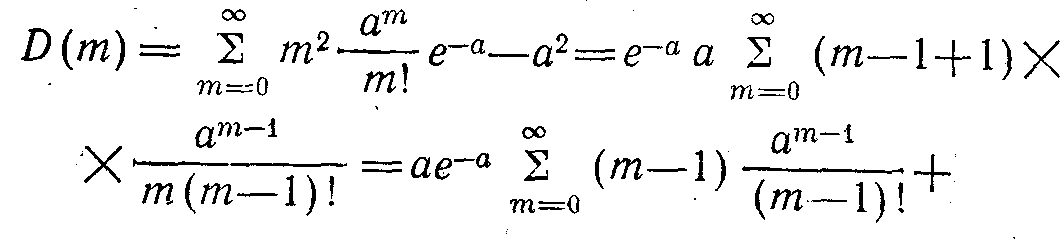
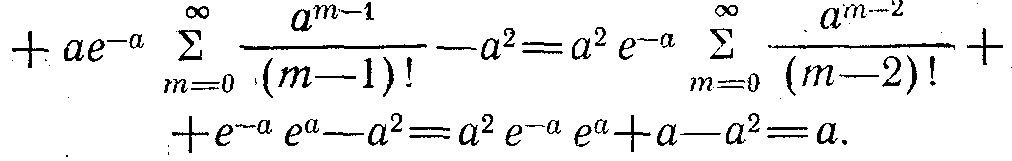
Міне, осылайша Пуассон заңы үшін математикалық нәтиже сандық жағынан дисперсияға тең келеді:

Р(m, а) функциясы m < =|a| үшін өте үлкен.

λ t –а шамалығы шағын болғанда таратылу құбылысы координат басына жақын шоғырланады.

Ол кездейсоқ шаманың (кейбір оқиғалардың пайда болу қатары) m мәнінен аз болатынының мүмкіндігі және оны мына теңдеуден көреміз:

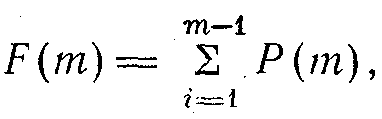
бұл жердегі Р(m) теңдеуімен шығарылады [15].

λ t –а шамалығы үлкен болғанда Пуассондық таратуды қалыпты таратумен шамалап мына параметрмен ауыстыруға болады:

Мұндайда [15] теңдеуін [16] теңдеуімен шамамен ауыстыруға болады:

мұндағы

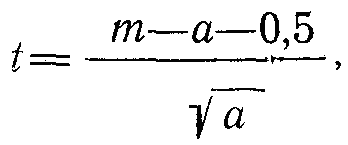
a F₀(t) - қалыпты таралу функциясы.

Пуассондық таралу іс жүзінде көп кездеседі. Бірнеше едәуір кең таралған оқиғаларды келтіреміз.

1) қарастырылған t уақыт ішінде станцияға келіп жеткен автомобильдер ағымы;

Үлгі. Қызмет көрсету станциясының жұмысын біраз уақыт байқау кезінде станцияға келіп жететін автомобильдердің мөлшері орта есеппен алғанда бір сағатта екеу болатыны белгілі болды. Станция жұмысының t = 3 сағатында станцияға 8 артық автомобильдің келу мүмкіндігін анықтау.

Шешім а = λ t = 2*3 =6 автомобиль; F (m<8) =

0,0149+0,0446+0,0892+

+0,1339+0,1606+0,1606+0,1377=0,1033 = 0,8448

2) t уақыт ағымында бірдей уақытта жұмыс істейтін n біртипті қайта қалпына келтірілмеген бөлшектер бар. Бұл бөлшектердің істен шығуына байланысты жұмыс істеу λ істен шығу қарқындылығымен бірге экспоненционалды заң бойынша таралған. Мүндай жағдайларда істен шыққан бөлшектердің кездейсоқ мөлшері төмендегі параметрмен Пуассон заңы бойынша таралған:

3) Істен шығу мүмкіндігі қарапайым болып келетін, бірақ қайта қалпына келтірілген бұйым берілген (жасалғаннан кейінгі кезеңде). Соңынша істен шығу жағдайының арасындағы уақыт арасы экспоненционалды тартылудан тұрады. Бұйымның істен шығуы Т₀ тең. Мұндай жағдайларда істен шығудың кездейсоқ мөлшері t уақыт ішінде төмендегі параметрмен Пуассон заңы бойынша таралған:

Үлгі. Жұмысқа жұмылдырылған кезеңі аяқталғаннан соң, істен шығуды шеттету берілген T_о = 100 мың үшін істен шығудың қарапайым ағымы орнатылды. Бұл автомобильдің 50 мың км ішіндегі жүрісі 2 істен шығуға әкелетін мүмкіндігін табу.

Шешім.

4) t уақыт ағымында бірдей уақытта жұмыс істейтін n біртипті қайта қалпына келтірілмеген бөлшектер сынаққа алынады. Бұл бұйымның істен шығуға дейін жұмыс жасауындағы таралу заңы белгісіз. Бір бұйымның t уақыт ішіндегі істен шығу мүмкіндігі белгілі және q-ға тең. Шамасы

q<=0,10. мұндай жағдайларда істен шыққан бұйымдардың t уақыт ішіндегі кездейсоқ мөлшері а = nq параметрімен бірге Пуассон заңы бойынша таралған.

5) N біртиптілі бұйымдардың партиясынан n бұйымынан бұйымынан тұратын таңдап алынды. Таңдалған бұйымды тексеру керек болады және артынша одан х ақаулықтар табылады. Барлық партия ішіндегі ақаулы бұйымдардың үлесі q тең екені белгілі. Олардың ара-қатынастары былай танылды:

Мұндай жағдайларда ақаулық бұйымдардың кездейсоқ мөлшері таңдау кезінде төмендегі параметрімен бірге Пуассон заңы бойынша таралған.

Ұсынылатын әдебиеттер / 3,4,6 /

.СДЖ арналған бақылау тапсырмалары / 3,4,6 /

1 КТ құрылымдарын сынау/бақылау/ түрлері

2 Ықтималдық қағаз және оның міндеті

3 Қалыпты бөліну заңының ықтималдық межелігін/шкаласын/ салу

4 Экспоненциалдық және Вейбулл заңдарының ықтималдық межеліктерін/шкалаларын/ салу

5 Үлестірілім параметрлері мен сенімділік көрсеткіштерін аралықпен бағалаудың ерекшеліктері

6 Кешенді көрсеткіштерді бағалайтын математикалық байланыстар

5-тақырып Көлік техникасының ұзақмерзімділігін анықтауға арналған аяқталмаған сынақтардың нәтижесін өңдеу – 2 сағат

Дәрістің жоспары

1 Пайдаланудағы КТ-ның сенімділігін басқару әдістері

2 Айырбастау жүйелері, ағындағы жөндеу түрлері

3 Аяқталмаған сынақтардың ерекшеліктері және олардың мәліметтері бойынша сенімділік параметрлерін есептеу

4 Статистикалық мәліметтерді өңдеуге ықтималдық қағаздарды қолдану

5 Толық жиынтық сипаттамаларының сенімдік аралығы

Беріктікке байланысты ең сенімді мәліметтерді әлі қанау шарттарындағы машиналардысынау мен қадағалау нәтижелерінен алады. Сондықтан беріктіктің бірінші ақпаратын статистикалық өндеу әдістері машина беріктігін дұрыс бағалаудағы және есептік жұмыстардың көлемін кішірейтудегі үлкен тәжірибелік мәнге ие.

Кейбір белгілер бойынша біріктіруге болатын заттар немесе құбылыстар тобын негізгі жиынтық деп атайды. Негізгі жиынтық көлемі шектеулі немесе шектеусіз болуы мүмкін. Таңдалмалы жиынтық болып сынақтар мен қадағалауларға ұшыраған негізгі жиынтық бөлігі. Мысалы, зауытта бір типті машиналар сериясының 10 мың данасы шығарылған – бұл негізгі жиынтық. Бұл машиналардың беріктігін анықтау үшін сынақтарға 10 машина ұшыраған – бұл таңдалмалы жиынтық.

Негізгі жиынтықтың сандық сипаттамалары – кездейсоқ емес шама, ал таңдалмалы жинтықтың сандық сипаттамалары – кездейсоқ. Біз тәжірибеде әрқашанда таңдалмалы сынақтармен және бақылаумен жұмыс істейміз. Олардың мәні неде?

Сынаулардың таңдалмалы әдісі кездейсоқ сұрыптау негізінде алынған элементтрдің тек қана құрастырушылар бөліктерін сынау немесе қадағалау кезінде негізгі жиынтықтың біріктірілген сипаттамаларын орнатуда қорытындалады. 10 машинаны сынау нәтижесінде біз барлық серияның беріктігін, яғни негізгі жиынтықты бағалаймыз немесе анықтаймыз.

Сынаулардың таңадлмалы әдісінің мүмкіндіктері үлкен сандар заңында негізделген, онда “тәжірибелердің үлкен санында анықталған белгінің орташа шамасы оның математикалық күтіміне жуықтайды” делінген. Тәжірибеде бұл әдіс үлкен мәнге ие:

— тәжірибелер көлемі азаяды және жеңілдетіледі, уақыт үнемделеді;

— бақылау мен тәжірибелер құны төмендейді және т.б.

Таңдалмалы орташаны есептеу

«Мүмкіндік теориясы» курсынан таңдалмалы орташа негізгі жиынтықтың математикалық күтудің ауқаттылық және жылжымайтын бағасы екені белгілі. Параметр бағасы, ауқаттылық және оның жылжымайтындығы дегеніміз не?

Шектелген сандар мен тәжірибелер негізінде есептелген кездейсоқ шаманың ізделінетін параметрінің кез келген мәні әрқашан да кездейсоқ элементіне ие болады. Мұндай параметрдің жуық мәнін статистикада параметр бағасы деп атайды. Егер тәжірибелердің саны көтерілгенмен параметр бағасы параметрдің өзіне жуықтаса, онда мұндай баға ауқаттылық болып табылады. Егер біз параметр бағасын қолдана отырып, жоғарылату немесе төмендету жағына қарай жүйелік қате жібермесек, онда мұндай баға жылжымайтын болып табылады.

Осы барлық қасиеттермен математикалық күту бағасы – кездейсоқ шаманың орташа арифметикалық мәні иеленеді. Бірақ таңдау және таңдалмалы орташаның есептелуі дұрыс жүргізілген деген шартта әділ болады.

Тәжірибеде жиі таңдалмалы орташаны есептеу барысында қателіктер жібереді. Есептеу дұрыстығын қарастырайық.

Негізгі жиынтық A₁, А₂, А₃, ..., А_n бөлек станоктар бір типті өнімінен тұрсын делік. Әрбір станок өнімінің саны сәйкес N_A, N_A2, N_A3, ...,N_An тең. Тәжірибелер үшін әрбір станок өнімінен А_n — n_А, A₂ — n_A2 және т.б. алнады.

Сынақтардың келесі нәтижелері алынды:

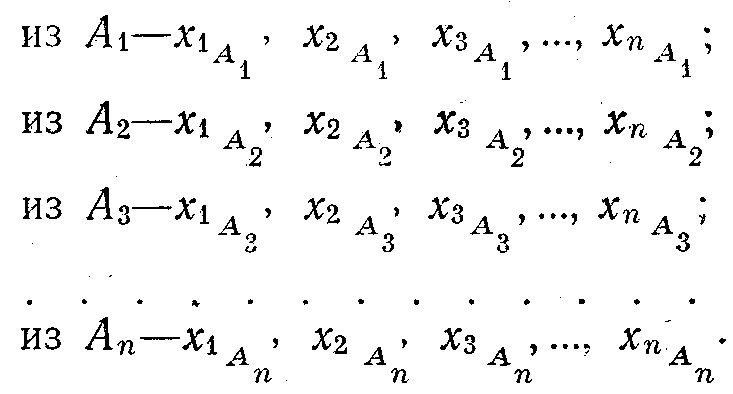
Таңдалмалы орташаны есептеу талап етіледі.

Әрбір партия шектерінде орташа мәнді есептейміз:

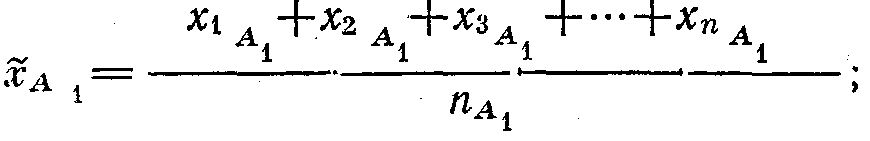
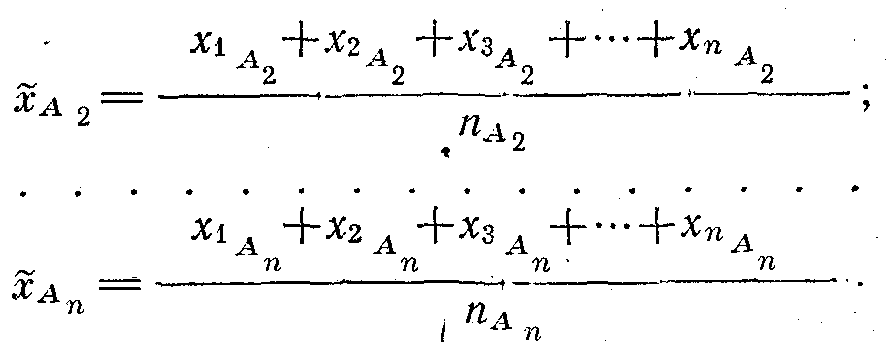
Таңдалмалы орташаны келесі формула арқылы анықтаймыз:

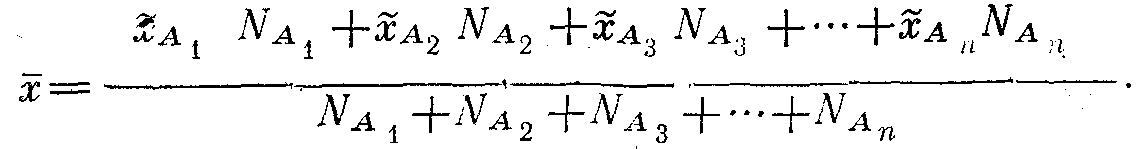
Кейде қате таңдалмалы орташаны былай анықтайды:

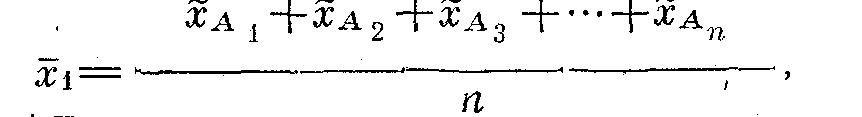
Мұндай қателікті жібермеу үшін таңдалмалы орташаны негізгі жиынтықтағы бөліктердің саны бойынша қайта өлшеу қажет (егер сұрптау бөлек өткізілсе).

Таңдалмалы дисперсияны есептеу

Келесі формула бойынша анықталған таңдалмалы дисперсия

δ² негізгі дисперсиясынан бірнеше кіші. n таңдау санының өсуінен S² δ²-қа жуықтайды және п—>∞ болғанда

S² = δ²

Сондықтан тәжірибеде негізгі дисперсияны таңдалмалы бойынша бағалағанда, соңғысын келесі формула бойынша есептейді:

S² = δ²

Егер — таңдалмалы орташа және кездейсоқ шамалардың таңдалмалы дисперсиясы x_1i (i = 1, 2, 3 …, n₁) — таңдалмалы орташа және шамалардың таңдалмалы орташасы X₂i (i = 1, 2, 3,...; n₂), онда біріктірілген таңдаудың таңдалмалы дисперсиясы келесі мәнге ие

мұндағы х келесі формула бойынша анықталады:

ШҰҒЫЛ БӨЛІНЕТІН ТӘЖІРИБЕЛЕР НӘТИЖЕЛЕРІНІҢ ҚАБЫЛДАМАУ КРИТЕРИЙЛЕРІ

Өте жиі өнімнің беріктігін сынақтан өткізген кезде тәжірибелер шарттарының тұрақсыздығымен, өнімнің сапасымен және басқа да көптеген факторлармен шартталған нәтижелерде үлкен қашықтылық байқалады. Оның өзінде қалғандарынан өзінің шамасы бойынша шұғыл бөлінетін бірлік мәндерді алынуы мүмкін. Егер мұндай нәтиже дөрекі қателіктен болғаны белгілі болса, онда оны анализ кезінде алып тастау керек. Ал бір немесе бірнеше нәтижелер қате алынды деген тек қана күдіктену болса, оны тексеру керек. Тексерудің бірнеше тәсілдері бар:

1. Үш орташа квадратты ауытқу ережесі.

2. Мәннің берілген деңгейіндегі мүмкіндік интегралын қолдану

3. Ирвин ережесі.

Бірінші әдісті қарастырайық (кесте 3).

6,35 шамасын берген 20 нәтижесі қалғандарынан біршама ерекшеленетіндіктенкүдік тудырады. Біздің күдіктенуіміздің дұрыстығын тексерейік.

Күдіктену нәтижесін есептемей орташа мәнді есептейміз (6,35-ді алып тастаймыз):

Тағы да күдіктену нәтижесін есептемей орташа квадраттық ауытқуды есептейміз:

Егер кұдіктелетін нәтиже ie±3S интервал шектерінен шықса, онда тәжірибе қате болып саналады және анализ кезінде оны алып тастау керек. Біздің жағдайымызда жіберілетін ауытқу 1,47 – 6,17 құрайд, ал 6,35 нәтижесі интервалдан шығып кетеді, сондықтан оны анализ кезінде алып тастау керек.

Егер бірнеше күдіктену мәліметтері болса, онда х және S бұл мәліметтерсіз анықтайды, сосын келтірілген сұлба бойынша әрқайсысын бағалайды.

МАШИНА БЕРІКТІГІ БОЙЫНША ТӘЖІРИБЕЛІК МӘЛІМЕТТЕРДІ ӨҢДЕУ КЕЗІНДЕ ЕҢ КІШІ КВАДРАТТАР ӘДІСІН ҚОЛДАНУ

Кейбір у шамасының х шамасынан тәуелділігін анықтау мақсатымен тәжірибе жүргізілсін, мысалы, қабылдамау мүмкіндігі мен машина жүрісінің тәелділігі.

у және х шамалары функционалды тәуелділікпен байланысқан делік

Y = f (x)

Тәжірибеден бұл тәуелділіктің түрін анықтау қажет.

Тәжірибелер нәтижесінде біз эксперименталды нүктелер қатарын алдық және оларды координаттар торына түсірдік делік. Әдетте мұндай графикта эксперименталдық нүктелер көрінетін жалпы заңдылықтан біршама қашықтылықпен орналастырылады. Бұл ауытқулар әрбір тәжірибе кезіндегі шарасыз өлшеу қателерімен байланысты. у-тің х-тен тәуелділігінің жалпы тенденциясын мүмкіндік бойынша дәл көрсететіндей және тәжірибенің өзінің шарасыз қателіктерімен байланысқан кездейсоқ заңды емес ауытқуларды тегістейтіндей етіп, тәжірибелік нүктелер бойынша график құру дұрыс болады. Мысалы, тәжірибелік нүктелердің орналасуының сыртқы түрі бойынша (сурет 9) у-тің х-тен тәуелділігін сызықты деп қабылдауға болады. Бұл нүктелер бойынша сансыз көп түзулер жүргізуге болады. Бірақ у-тің х-тен тәуелділік тенденциясын жақсырақ түрде көрсететін бір жалғыз түзу бар. Бұл жалғыз түзуді қалай табу керек?