Сур. 4. Пайдалану жағдайындағы қозғалтқыштың қабыл алмаулар ағынының өзгеруі

Шамасы, машинаның осы жұмыс үшін қабыл алмауларының орташа саны оның элементтерінің орташа сандарының сомасына тең болады:

Жұмыс бойынша осы өрнекте дифференциялап, мынаны аламыз:

немесе

яғни машинаның қабыл алмаулар ағынының параметрі оның элементтерін құрайтын қабыл алмаулар ағынының параметрлерінің сомасына тең болады.

Егер де қабыл алмаулар ағынының параметрі тұрақты болса, онда мұндай ағын стационарлы деп аталады. Бұл қасиетке қабыл алмаулар ағынының өзгеру қисығының екінші учаскесі ие болады.

Машиналар сенімділігі көрсеткіштерін білу әр түрлі есептеулер, сонымен бірге запасты бөліктердегі қажеттіліктерді есептеу жүргізуге мүмкіндік береді. Δ t жұмысы үшін п_зб запасты бөліктердің саны мынаған тең болады:

ω(t) функция екендігін ескере отырып, t₁-ден t₂-ге дейінгі шектердегі жеткілікті үлкен жұмысы үшін аламыз:

4-суретте Мәскеу қаласының пайдалану жағдайларындағы ЗИЛ-130 қозғалтқышының қабыл алмаулар ағынының параметрлерінің өзгеру тәуелділігі келтірілген. Жүріс километрімен өрнектелетін автомобильдерге қатысты 1 белгісі енгізілген.

Ұсынылатын әдебиеттер / 3,4,6 /

.СДЖ арналған бақылау тапсырмалары / 3,4,6 /

1 Істен шығудың дифференциалдық үлестірім заңы

2 Бірінші істен шығуына байланысты объекттер сенімділігінің сипаттамалары

3 Істен шығу ағынының сипаттамасы

4 Істен шығу ағынының параметрі

5 Сенімділік көрсеткіштерін қолданатын инженерлік есептер түрлері

3-тақырып Көлік техникасының сенімділік көрсеткіштерін анықтайтын кездейсоқ шамалардың таралым/үлестірім/ заңдары - 8 сағат

Дәрістің жоспары

1 Техникалық жүйелердің тозуы. Тозу түрлерінің жіктелуі, тозудың көрсеткіштері, заңдылықтары және сипаттамалары

1 КТ сенімділігі теориясында жиі қолданылатын теориялық үлестірілім заңдары

2 Экспоненциалдық үлестірілім заңы

3 Қалыпты үлестірілім заңы

4 Логарифмдік қалыпты үлестірілім

5 Вейбулл үлестірілім заңы

6 Пуассон үлестірілім заңы

Ықтималдық теориясы әдісіне сүйене отырып, машиналардың істен шығу заңдылығын анықтаймыз. Машиналарды пайдаланудан және зерттеу нәтижелерінен алынған істен шығу жайындағы тәжірибелі мәліметтер алынады.

Ықтималдық теориясында кездейсоқ шамаларды тарату заңының көп түрі белгілі. Машиналардың пайдалаудағы беріктігін сараптауда қолдануда жиі кездесетін заңдылықтарды қарастырамыз.

Экспоненциальды заңдылықта істен шығусыз жұмыс ықтималдығы келесі түрде сипатталынады

мұнда λ — осы заңның параметрі — істен шығу интенсивтілігі, оның өлшемділігі, істен шығу қызмет ету бірлігінде.

Істен шығу ықтималдығы мынаған тең

Істен шығу жиілігі —

Істен шығуға дейін қызмет ету—

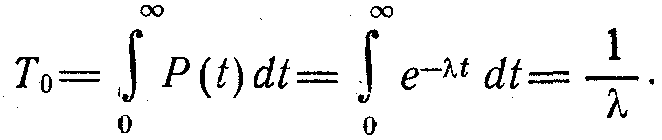
Экспоненциальды заңдылықта орташа ауытқу мынаған тең:

вариация коэффициенті —

Қызмет ету барысында t=T₀ беріктік е есеге азаяды:

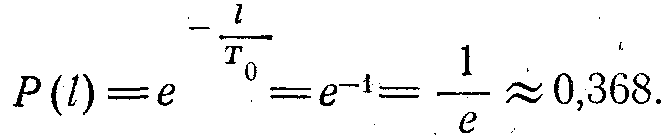
Мысалы. Істен шығудың интенсивтілігі λ = 0,005 = const (ІСТЕН ШЫҒУ / 1000 км.)

Істен шығу экспоненциальды заңдылыққа бағынатыны белгілі болса, автомобилдін 10 мың км-ді істен шығусыз жүру ықтималдығын анықтау.

Онда 10 мың км-де 100-ден 5 автомобильдің істен шығуын күтуге болады. Кез келген 10 мың км. үшін сенімділік солай болады. 150 мың км. жүруге сенімділік қандай болады?

150 және 160 мың км. жүріс аралығындағы 10 км.дегі істен шығусыз жұмыс істеу сенімділігі қандай?

қайтадан

істен шығуға дейін қызмет ету мынаған тең:

Сонымен қатар кері теңдеуді де шешуге болады.

Қанша жүргенде 100 автокөліктің 10-ы істен шығады, егер Р(l) = 0,9?

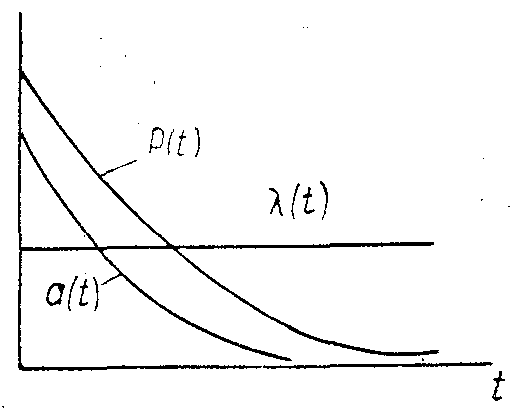
5-ші сурет. Экспоненциальды заңдылығында машиналар сенімділігінің сипаттамасы

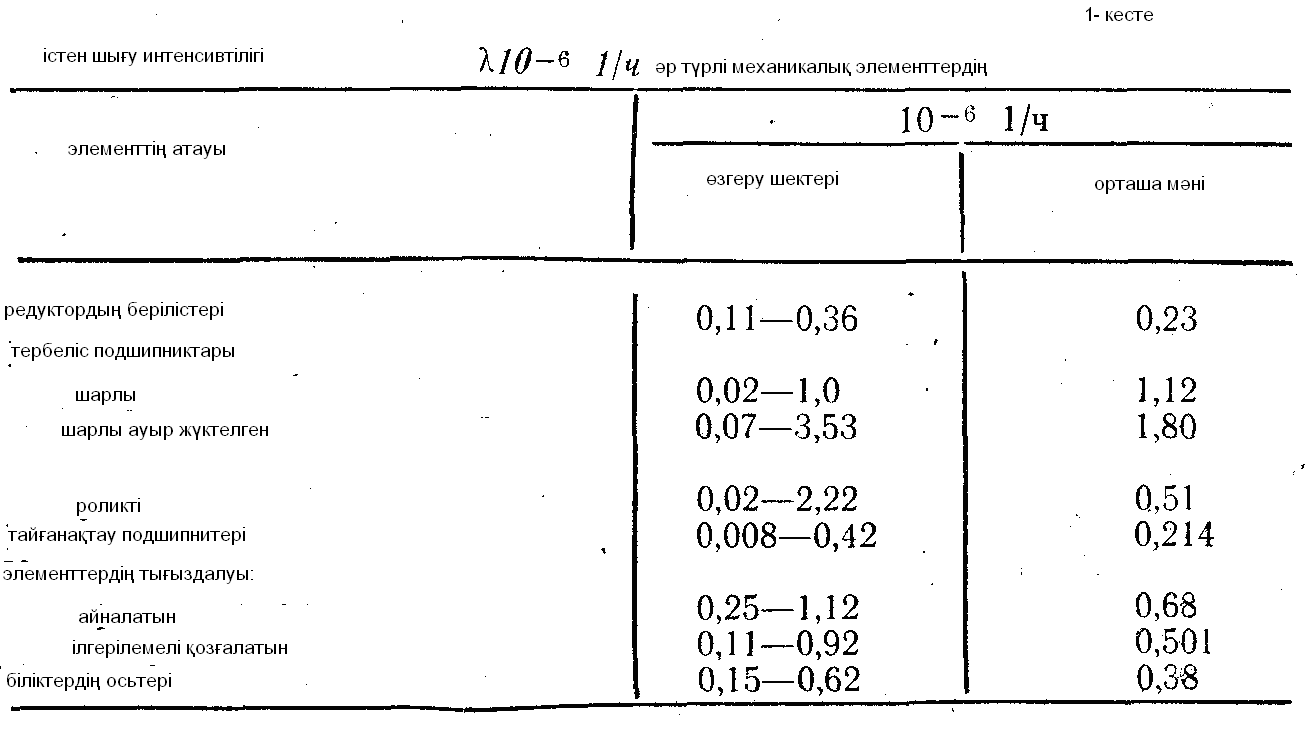
Механикалық элементтердің істен шығуының интенсивтілігінің шынайы шамасы жайында түсінік алу үшін[10] әдебиеттен кейбір мысаалдар келтіреміз.

Экспоненциальды заңдылық машиналардың келесі элементтерінің істен шығуын жеткілікті жақсы сипаттайды:

— радиоэлектронды аппаратуралардың көп қалпына келтірілмейтін элементтерінің істен шығуға дейінгі қызмет көрсетуі;

— қарапайым істен шығулар ағымындағы көршілес істен шығулар арасындағы қызмет көрсету;

— жағдайлар қатарында істен шығудан кейін қалпына келтіру; т.б.

5-ші суретте пайдалану заңдылығында машиналардың сенімділігінің сипаттамасы келтірілген.

Машиналардың элементтерінің кездейсоқ факторлардың бір уақытта әрекеттесуінен

пайда болатын істен шығулары (динамикалық жүктеме, ескіру, материалдың ескіруі, коррозия т.б.) жақын және қалыпта заңдылық бойынша сипатталынады.

Тарату тығыздыңы (істен шығулар жиілігі) қалыпты заңдылыұта мына формуламен анықталынады:

мұнда δ²— дисперсия;

а— математикалық күтімі (біздің жағдайда а ≈ T₀— істен шығуға дейінгі орташа қызмет көрсетуі).

Жеке жағдайды қарастырайық, а=0 болғанда, а=1. Таратудың тығыздығын біраз уақыттан соң белгілейік. Бұл жағдайда (11) шешім былай болады:

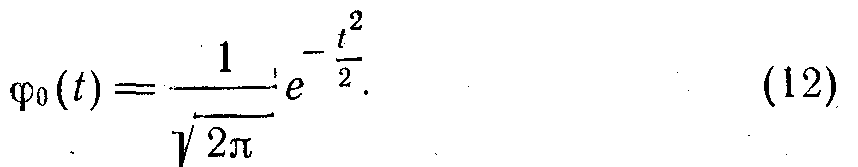
φ₀ (t) функциясы үшін құрылған кестені ықтималдық теориясы жайындағы барлық кітаптардан кездестіруге болады:

t аргументінің кері мәнінде (12) теңдеуінен:

а және δ кез келген жағдайы үшін (12) функциясының кестесінің көмегімен қалыпты таратудың тығыздын оңай есептеуге болады.

(11) және (12) теңдеуінен:

Қалыпты таратудың интегралды функциясы мына теңдеумен алынады (істен шығу мүмкіндігі):

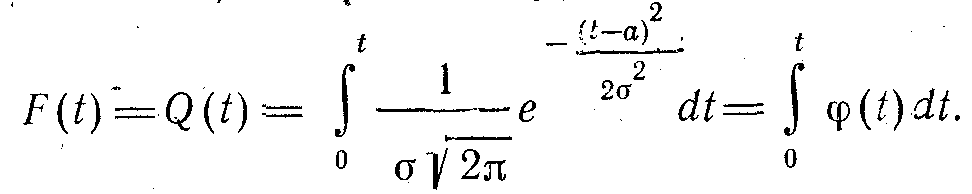
Жекелеген жағдайда, а=0 және δ=1 болғанда, онда қалыптасқан таратуда мынаны аламыз:

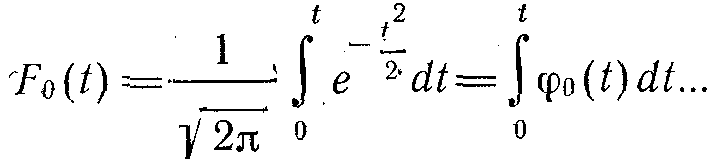
F₀(t) функциясы табуляцияланған, сондықтан, F(t) функциясын жалпы жағдайда былай табады:

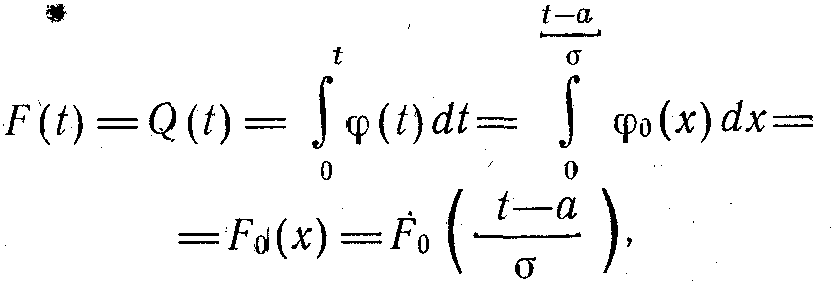
Егер t істен шығуға дейінгі қызмет ету қалыпты заңдылық бойынша таралса, онда істен шығудың болмау ықтималдығы 0 мен t аралығында мына формуламен табылады:

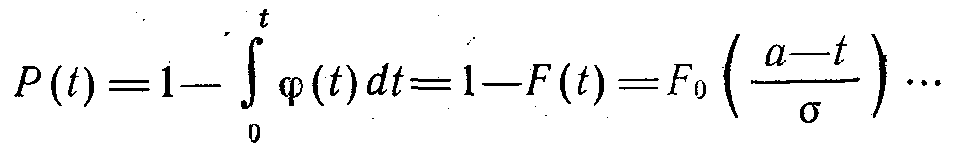
Кері мән үшін және

F₀(x) функциясы мына формуламен табылады:

Істен шығудың интенсивтілігі мына теңдеумен табылады:

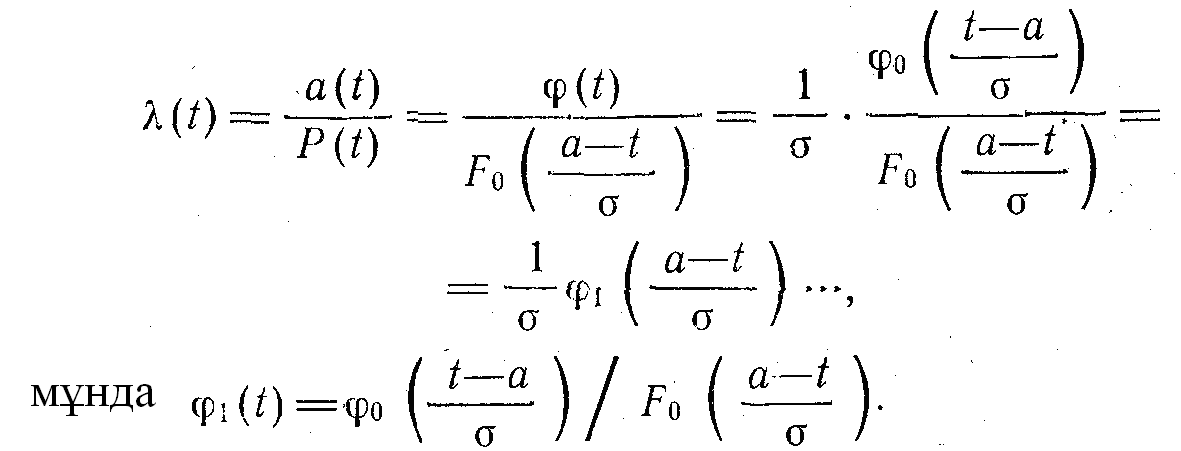
φ₁ (t) функциясының кестесі [16] кітапта келтіріледі.

Функция көмегімен t₁ -ден t₂ –ге дейінгі берліген қызмет көрсету интервалында істен шығудың пайда болу ықтималдығы оңай анықталады:

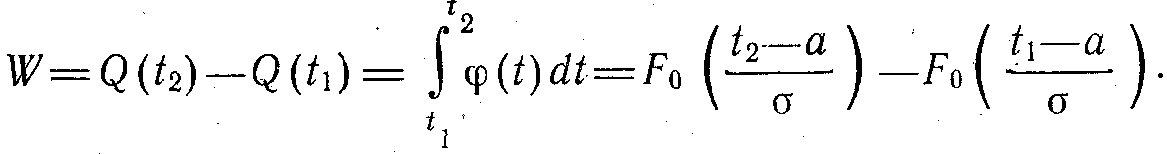
φ₀ (t) және F₀ (t) функцияларының [16] кестелерінің элементтерін жазып алып және келесі тапсырманы шешеміз:

2-щі кесте

	0,3	0,4	0,5	1,0	3,0
	0,3814	0,3683	0,3521	0,2420	0,004432
	0	1	2	3	4
	0,5	0,8413	0,9772	0,9986	1,000

Мысал. ГАЗ «Волга» автокөлігінің рессорының г таксоматорлы паркінің жұмыс істеу шартында істен шықты деп есептейік. Горьки T₀ =70 мың км және S = 20 мың. км парметрлерімен қалыпты заңға бағынады. l = 50 мың км.жүргендегі рессордың сенімділігің барлық сипаттамасын табу қажет.

Шешу. T₀ ≈ a, S ≈ δ теңестіреміз. Істен шығусыз жұмыс істеу ықтималдығы мынаған тең

Істен шығу жиілігі –

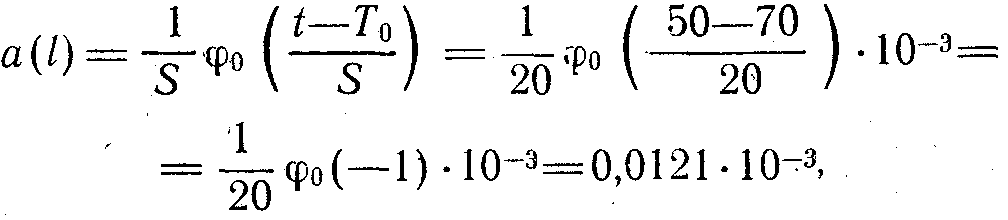
Сенімділікке прктикалық тапсырманы шеу барысында машинаның істен шығу ықтималдығына берілген мәнге немесе істен шығусыз қызметін анықтау қажеттілігі туындайды. Мұндай тапсырмаларды квантили кестесін қолдану арқылы шешкен оңай.

Квантили — бұл функцияның аргументінің мәні, ықтималдықтың берілген функциясының мәніне жауап береді.

Қалыпты заңдылыңта істен шығу ықтималдығының функциясын белгілейміз

Қалыпты заңдылықтың квантилей кестесінде [16] квантилей и_р мәндері р>0,5 ықтималдығы үшін берілген. р<0,5 ықтималдығы үшін оларды мына теңдеу арқылы беруге болады:

мысал. Автокөліктің рессорының сынулары 20% аспайтын жүрімін табу, егер,

болса.