Пирсон хи-квадратының келісім өлшемі

Бұл өлшем бойынша таратылу шамасы былайша есептеледі:

мұндағы m_i* и m_i- кездейсоқ шаманың өзгеру аралығы немесе разрядтардағы оқиғалардың тәжірибелік және теориялық сәйкесті саны; n – разрядтар (аралықтар) саны.

х²жіктеу еркіндік дәрежесінің саны деп аталатын K параметріне тәуелді болады. K еркіндік дәрежесінің саны қарастырылатын теориялық заңда көрсетілген, тәуелсіздік байланыс саны n минус разрядтар (интервалдар) санына тең келеді.

Мұның үлгісі ретінде мыналар бола алады:

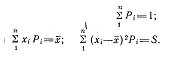
Пирсонның хи-квадратын жіктеу үшін арнайы кестелер құрастырылған және одан хи-квадрат.... және K еркіндік дәрежесінің санының шамасы бойынша келісім мүмкіндігінің мәнін алуға болады.

.....жіктеу теориялық және тәжірибелік жіктеудің келісімдік дәрежесін бағалауға мүмкіндік береді. Егер де берілген .....шама мен еркіндік дәрежесіне келісімдік мүмкіндігі 0,05 немесе 0,1 аз болса, онда қабылданған теориялық заң тәжірибелік жіктеуге тең келмейді, ал егер де көп болса, онда тәжірибелік жіктелуге қарама-қайшы келмейді. Пирсонның хи-квадратының өлшемін теориялық және тәжірибелік жіктеу келісімінің бағасына қарай қолдану схемасы мынаған тең келеді:

• тарату шамасы .....формуласы бойынша анықталады (33);

• еркіндік дәрежесінің саны былай анықталады:

мұндағы r - байланыстардың саны,

n - статистикалық материалдарды өңдеу кезінде қабылданған разрядтар (интервалдар) саны;

- K және х² бойынша Пирсонның хи-квадратын жіктеу кестесінде Ρ келісім мүмкіндігі анықталады. Егер де Ρ>0,1 немесе Ρ>0,05 болса, онда қарастырылатын теориялық заң қабылданады.

х² өлшемін пайдалануда жекелеген разрядтарда (интервалдарда) тәжірибелердің жалпы саны қандай көп болса, m_і оқиғалардың (істен шығудың) жалпы саны сондай көп болуы мүмкін екенін . Іс жүзінде әрбір разрядта 5-10 оқиғалардың (істен шығудың) болғаны жөн. Егер де жекелеген разрядтардағы оқиғалардың саны өте аз болса (1-2), онда бірнеше разрядтарды біреуге біріктірген жөн.

Колмогоровтың келісімдік өлшемі

Теориялық және тәжірибелік жіктеулер арасындағы тарату шамасы ретінде Колмогоров Q* (t) жіктеудің тәжірибелік функциялары мен сәйкес келетін теориялық функцияның арасында әр түрлі модульдің ең көп мәнін қарастырады.

Одан соң шаманы анықтайды:

мұндағы п – тәжірибелер (байқаулар) саны.

λ шамасы бойынша (13 кесте) келісім мүмкіндігін Р (λ) табамыз. Егер де (λ) мүмкіндігі 0,05 немесе 0,1 кем болса, онда қарастырылатын теориялық заң оны сәйкес келмейтін тәжірибелі деректер ретінде алып тастайды.

Колмогоровтың келісімдік өлшемін аталмыш тәжірибелі жіктеуге арналған теориялық функциясының түрі мен оған кіретін барлық параметрлер белгілі болған жағдайда қолданған мақсатқа сай болады.

Теориялық заңды тәжірибелік жіктеудің нәтижелілігін төмендегі үлгі бойынша қарастырамыз: