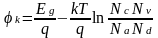- •1.Аналитические выражения для вах р-n-переходов
- •2.Входное сопротивление, коэффициент усиления по току, коэффициент усиления по напряжению, коэффициент усиления по мощности биполярного транзистора на низкой частоте в схеме с общей базой
- •3.Лавинный пробой электронно-дырочного перехода. Тепловой пробой.
- •Полевые транзисторы
- •7.Эффект оттеснения тока эмиттера на край эмиттера.
- •8.Параметры моп - транзистора. (Статические параметры; Дифференциальные параметры; Электрофизические параметры (подвижность и механизмы рассеяния носителей в канале).
- •9. Статические вах биполярного транзистора.
- •10 Резкий несимметричный электронно-дырочный переход в состоянии теплового равновесия
- •11 Статические вольт-амперные характеристики биполярного транзистора в схеме с общим эмиттером
- •12.Высота потенциального барьера (q ). Зависимость q от температуры (т), концентрации примеси (n) и ширины запрещённой зоны
- •13. Электрические зонные диаграммы, поясняющие случаи обогащения, обеднения слабой и сильной инверсии моп структур.
- •14 Граничная концентрация неосновных носителей заряда в базе электронно-дырочного перехода
- •15. Переходные процессы в диоде:
- •16. Величина порогового напряжения моп-транзистора, и пути его регулирования:
- •17. Туннельный пробой диода. Сравнительный анализ туннельного и лавинного пробоя:
- •18.Частотные свойства бт
- •19.Эффект Эрли и его следствия
- •21.Импульсные свойства биполярного транзистора: случай малого и большого сигналов.
- •Импульсные свойства бт при малом сигнале
- •Импульсный режим работы бт при большом сигнале
- •22.Модель Эберса-Молла.
- •23.Реальные моп-структуры с n и p подложками. Энергетические зонные диаграммы, разности работ выхода металл – затвора – полупроводник (моп структур) с Al и поликремниевым затворами
- •24. Барьерная ёмкость диода
- •25. Электронно-дырочный переход при нарушении теплового равновесия. Токи инжекции и экстракции
- •26. Генерация и рекомбинация носителей в - -переходе
- •27. Коэффициент передачи тока эмиттера идеализированной модели биполярного транзистора.
- •Виды пробоя биполярного транзистора (смыкание эмиттерного и коллекторного перехода, лавинный пробой, вторичный пробой)
- •База отключена
- •Диффузионная ёмкость диода
- •Барьер Шотки. Диод Шотки. Транзистор Шотки Барьер Шоттки
- •Диод Шоттки
- •Вопрос 31. Распределение концентрации неосновных носителей в базе(случай тонкой базы).
- •Вопрос 32. Аналитические выражения вах электронно-дырочного перехода(случай тонкой базы).
- •Вопрос 33. Распределение потоков носителей в реальной одномерной бт
- •34. Особенности работы p-n перехода при высоком уровне инжекции вуи
- •35. Биполярные транзисторы
- •36. Образование электронно-дырочного (р-n) перехода
- •37. Зависимость коэффициентов передачи тока от тока эмиттера
- •38. Распределение концентрации неосновных носителей в базе (общий случай)
- •40.Входное сопротивление, коэффициент усиления по току, коэффициент усиления по напряжению, коэффициент усиления по мощности биполярного транзистора на низкой частоте в схеме с общим коллектором
- •41 Характеристические частоты биполярного транзистора
36. Образование электронно-дырочного (р-n) перехода
Введем два монокристалла полупроводника, обладающих различными типами электропроводимости, в идеальный контакт. Процессы, происходящие в р-n-переходе, будем анализировать в диапазоне температур, при которых все примеси ионизированы. Объемы полупроводников электронейтральны, т.к. заряды связанных носителей (ионизированных доноров и акцепторов) уравновешиваются зарядами свободных носителей (соответственно электронов и дырок). Из-за наличия градиента концентрации основные свободные носители заряда будут диффундировать в соседние области, где они вблизи запишем границы рекомбинируют.
Около металлургической границы (м.г.) перехода, то есть в плоскости, где меняется тип преобладающей примеси, образуется двойной заряженный слой нескомпенсированных ионизированных акцепторов и доноров, поле которого (Eдифф) будет препятствовать дальнейшей диффузии. Этот слой шириной (xd) будем называть областью пространственного заряда (ОПЗ) или обедненным слоем. Из условия электронейтральности перехода:
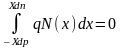
запишем: Na xdp = Nd xdn
Считаем, что в идеальном случае все напряжение, приложенное к р-n-переходу, падает на ОПЗ.
Вследствие наличия электрического поля между областями материала разных типов электропроводности образуется потенциальный барьер. Достижение равновесного состояния осуществляется за счет того, что диффузионные составляющие электронного JnD и дырочного JpD токов уравновешиваются движущимися в обратном направлении под действием Edif дрейфовыми составляющими токов JnE и JnE (рис. 1.1, б).
Высоту потенциального барьера р-n-перехода можно определить, исходя из следующих соображений. Когда обе области полупроводника находятся в равновесии, уровень Ферми должен быть постоянным в пределах всей системы, следовательно, высота потенциального барьера будет определяться положением уровня Ферми в n- и р-областях. Он эквивалентен разности работ выхода из этих отдельных областей, т.к. работы выхода из полупроводника определяется выражением:
qs = q + (EC – EF), где q— энергия сродства к электрону.
Р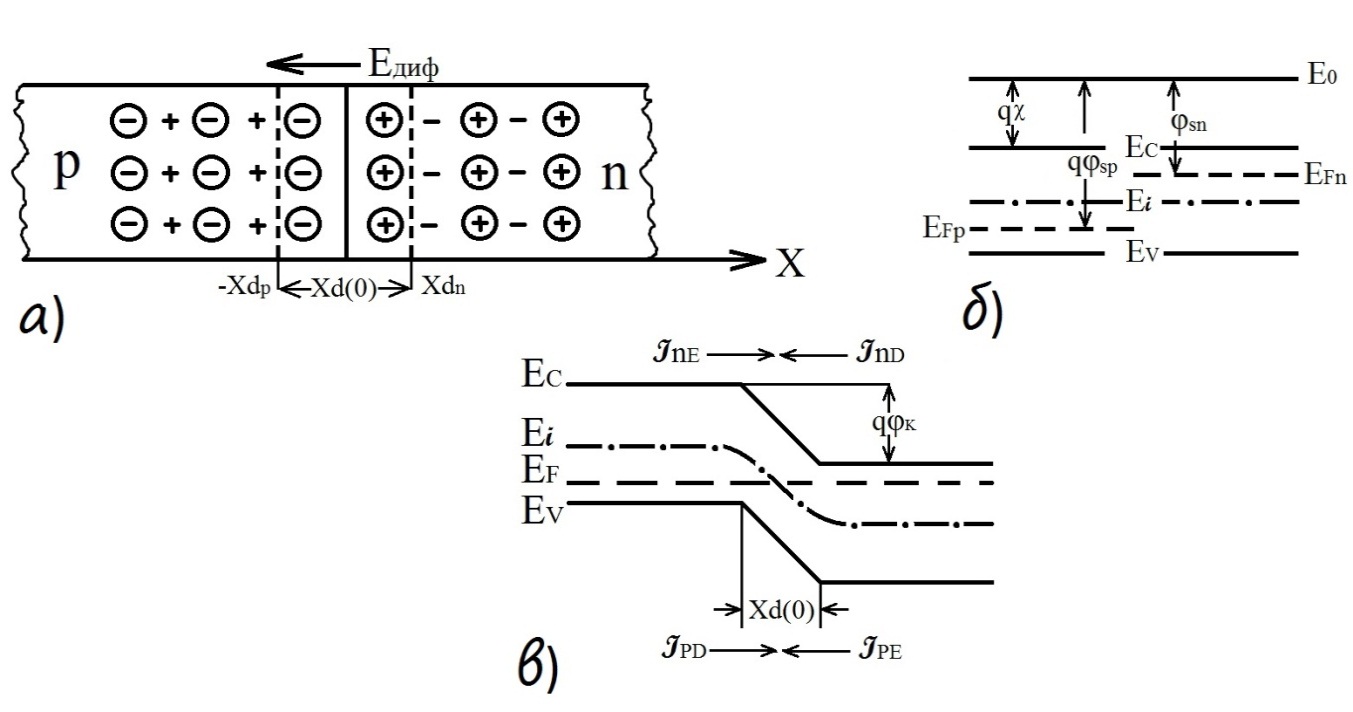 исунок
1.1 – Образование р-n-перехода
исунок
1.1 – Образование р-n-перехода
а — энергетическиезонные диаграммы р-n-полупроводников;
б — рисунок, поясняющий образование обедненного слоя;
в — энергетическая зонная диаграмма р-n-перехода.
“+”, “-” — свободные носители заряда(электроны и дырки, соответственно);
“+”, “-” — связанные носители заряда (ионизированные доноры и акцепторы, соответственно);
Итак,
qSp – qSn = qk = [ q + Ei +(Ei – EF)]p – – [ q + Ei – (EF – Ei)]n = (Ei – EF)p + (EF – Ei)n. |
|
Известно
, что
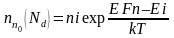 ,
,
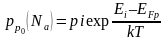 и
и
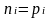 .
.
Следовательно,
|
|
а
контактная разность потенциалов 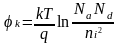 .
.
Или, полагая, что
|
|
Получим
|
|
Выражение можно записать иначе: зная,что ni2 = NcNv exp(–Eg/kT),
и считая, что Nс> Nd,a Nv> Na,
контактную разность потенциалов k запишем:
|
|
где Nc, Nv — эффективные плотности разрешенных состояний в свободной и валентной зонах, соответственно.
Из контактной разности потенциалов видно, что контактная разность потенциалов и высота потенциального барьера увеличиваются с ростом ширины запрещенной зоны полупроводника и концентрации примесей и уменьшаются с ростом температуры.

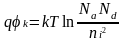 ,
,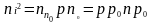 ,
,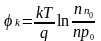
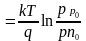 .
.