
- •ІнтеграЛи та їх застосування
- •Розділ I Невизначений інтеграл
- •2. Метод внесення функції під знак диференціала
- •3. Метод інтегрування частинами.
- •Метод заміни змінної.
- •5.Інтегрування раціональних дробів.
- •6.Інтегрування ірраціональних функцій
- •Інтеграли від тригонометричних функцій.
- •Визначені інтеграли
- •Невласні інтеграли
- •Застосування інтегралів
- •Знаходження довжини плоскої кривої
- •3.Знаходження площ поверхонь та об’ємів тіл обертання
- •4. Застосування інтегралів при розв'язанні задач механіки
- •ІнтеграЛи та їх застосування
Знаходження довжини плоскої кривої
Довжина
дуги гладкої плоскої кривої, заданої
рівнянням
![]() на відрізку
на відрізку
![]() ,
обчислюється за формулою
,
обчислюється за формулою
![]() .
(10)
.
(10)
Якщо ж крива задана параметрично:
![]() ,
,
![]() ,
,
![]() ,
,
то
 . (11)
. (11)
Крива може бути задана в полярній системі координат:
![]() ,
,
![]() .
.
Тоді
![]() .
(12)
.
(12)
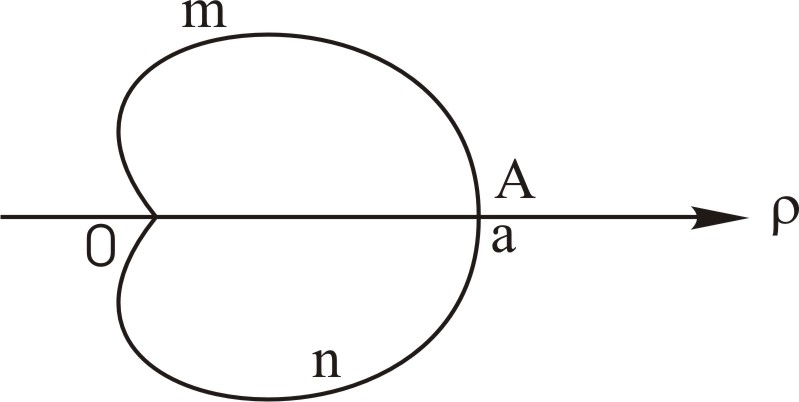
Задача 13. (13.1. а, б – 13.30. а, б.). Обчислити довжину дуги заданої плоскої кривої
Приклад
13.1 Знайти
довжину дуги лінії кардіоїди, що задана
рівнянням
![]() ,
,
![]() .
.
Рис. 11 |
Спочатку
знаходимо довжину дуги (AmO),
що описується при зміні кута
від 0 до
![]() :
:

Так
як
![]() при
при
![]() ,
то
,
то
![]() і
і
![]() ,
,
![]() лін. од.
лін. од.
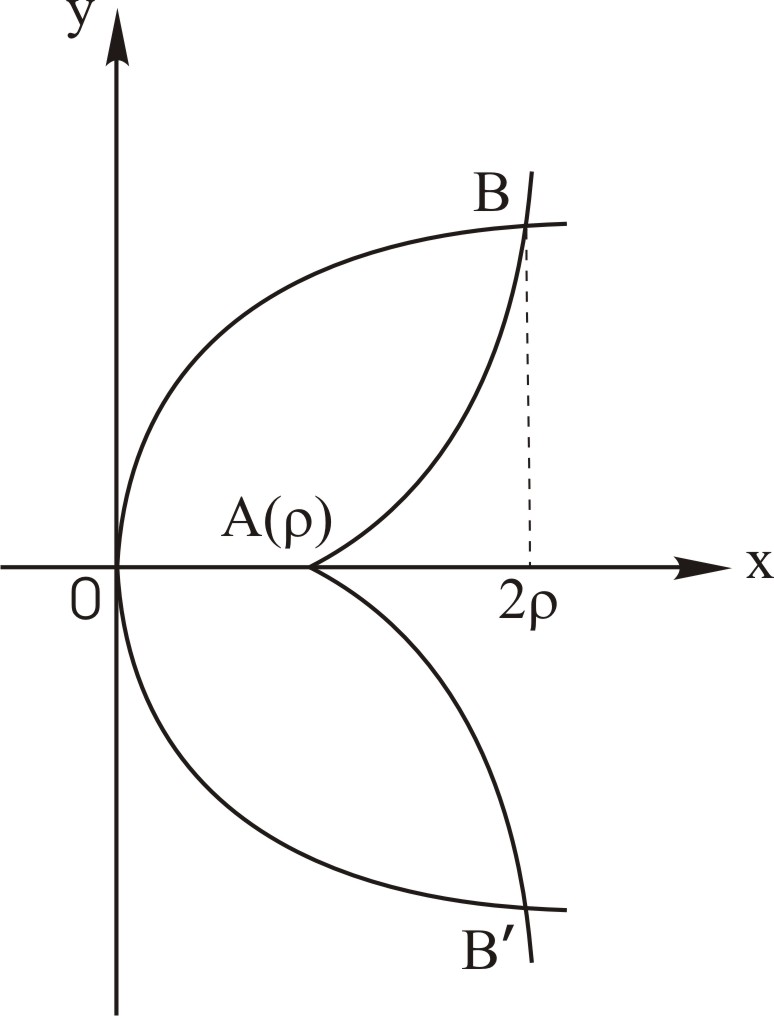
приклад
13.2. Обчислити
довжину дуги напівкубічної параболи
![]() ,
що вирізана параболою
,
що вирізана параболою
![]() .
.
Розв'язання.
Зробимо
схематичний рисунок (рис. 12) З рисунка
видно, що в задачі потрібно знайти
довжину дуги
![]() ,
що складається з двох симетричних
частин. Тому достатньо обчислити довжину
дуги АВ
і подвоїти результат. Для знаходження
меж інтегрування достатньо знайти
абсцису точки В,
оскільки абсциса точки А
уже відома і рівна p.
Розв’яжемо систему рівнянь двох парабол:
,
що складається з двох симетричних
частин. Тому достатньо обчислити довжину
дуги АВ
і подвоїти результат. Для знаходження
меж інтегрування достатньо знайти
абсцису точки В,
оскільки абсциса точки А
уже відома і рівна p.
Розв’яжемо систему рівнянь двох парабол:
Р |

Отримали
кубічне рівняння, розв’язок якого
знаходимо підбором:
![]() .
.
Так
як функцію можна записати рівнянням
,
то для розв’язання задачі використовується
формула (10), де
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.

Зауваження. 1. якщо при обчисленні довжин дуг, межі інтегрування відомі, будувати рисунок не обов’язково.
2.
В деяких випадках при використанні
формули (10) доцільно в якості значення
функції покласти змінну x
і формула (10) матиме вигляд
![]() ,
де дуга кривої буде задана рівнянням
,
де дуга кривої буде задана рівнянням
![]() ,
,
![]() .
.
ЗАДАЧА 13. Індивідуальні завдання
1.
а)
|
б)
|
2.а)
|
б)
|
3.
а)
|
б) |
4
а)
|
б)
|
5.
а)
|
б)
|
6.
а)
|
б)
|
7.а) |
б) |
8.
а)
|
б)
|
9.
а)
|
б)
|
10.
а)
|
б)
|
11.
а)
|
б)
|
12.
а)
|
б)
|
13.а) |
б)
|
14.а)
|
б)
|
15.а) |
б)
|
16.
а)
|
б)
|
17.а) |
б) . |
18.
а) |
б)
|
19.а) |
б)
|
20.
а)
|
б)
|
21.
а)
|
б)
|
22.а) |
б)
|
23.
а)
|
б)
|
24.
а)
|
б)
,
|
25.
а)
|
б)
|
26.а) |
б)
|
27.а) |
б)
|
28.а) |
б)
|
29.а) |
б)
|
30.
а) |
б)
|

 ис.
12
ис.
12
 ,
,
 ,
,
 .
.
 ,
,
 .
.
 .
. .
.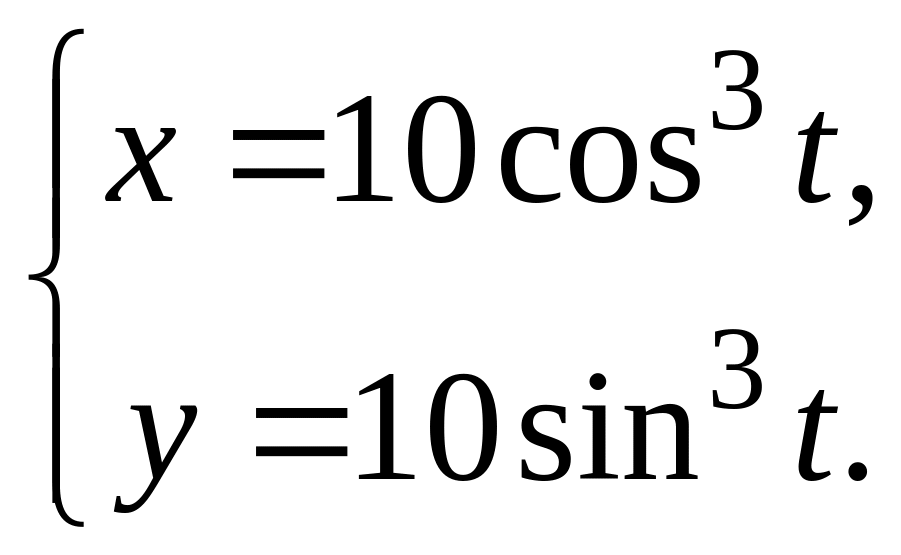
 .
.
 ,
,


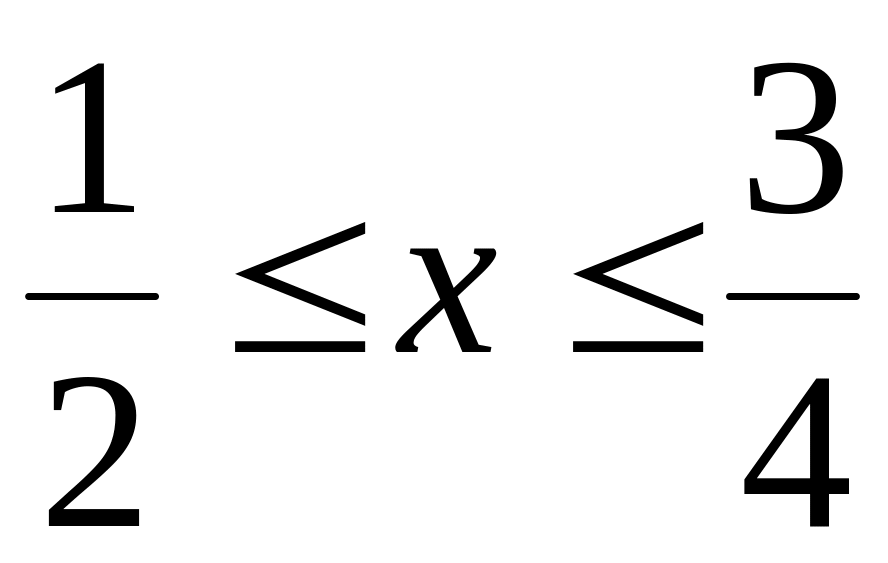 .
.
 .
. .
. .
. .
. ,
.
,
. .
. .
. .
. .
. .
.
 .
. .
. .
. ,
, ,
,
 .
. ,
,