Выравнивание по уравнению прямой

Уравнение прямой может быть выражено в виде следующей формулы:

y_t =a_o+a₁t,

где y_t – значение выровненного ряда;

a_o, a₁ – параметры прямой линии (которые необходимо вычислить);

t – показатель времени.

Задача состоит в том, чтобы фактические уровни ряда (у) заменить теоретическими (y_t).

Для расчета параметров прямой линии a_o и a₁ используем способ наименьших квадратов, который дает систему двух уравнений:

;

где n – число членов ряда;

у – фактические уровни ряда;

t – показатель времени.

Упрощенный расчет параметров уравнений заключается в переносе начала координат в середину ряда динамики (t=0). В этом случае упрощаются сами нормальные уравнения, кроме того, уменьшаются абсолютные значения величин, участвующих в расчете. Тогда системы нормальных уравнений для оценивания параметров прямой (у = a₀+a₁t) примут вид:

.

Решая систему относительно неизвестных параметров, получим величины параметров соответствующих полиномов.

Точечные и интервальные прогнозы

Прогнозирование по среднему абсолютному приросту ( ) — основано на предположении о равномерном изменении уровня (под равномерностью понимается стабильность абсолютных приростов). Экстраполяцию можно сделать по следующей формуле:

где — экстраполируемый уровень; (n+i) — номер этого уровня;

n — номер последнего уровня исследуемого периода, за который рассчитан;

i — срок прогноза (период упреждения).

Прогнозирование по среднему темпу роста осуществляется в случае, когда есть основание считать, что общая тенденция ряда характеризуется показательной (экспоненциальной) кривой. Для нахождения тенденции необходимо определить средний коэффициент роста (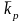 ), возведенный в степень, соответствующую периоду экстраполяции, т. е. по формуле:

где у_n — последний уровень ряда динамики; i — срок прогноза;

Наиболее распространенным методом прогнозирования считают аналитическое выражение тренда. При этом для выхода за границы исследуемого периода достаточно продолжить значения независимой переменной времени (t).

При таком подходе к прогнозированию предполагается, что размер уровня, характеризующего явление, формируется под воздействием множества факторов, причем не представляется возможным выделить отдельно их влияние. В связи с этим ход развития связывается не с какими-либо конкретными факторами, а с течением времени, т. е. у = f(t).

При выборе типа линии можно учитывать следующее:

1. прямая линия — если абсолютные приросты уровней ряда по своей величине колеблются около постоянной величины;

2. парабола второго порядка (полином) — если приросты приростов уровней (ускорения) колеблются около постоянной величины;

3. показательная функция (экспонента) — если уровни изменяются с приблизительно постоянным относительным приростом.

Экстраполяция дает возможность получить точечное значение прогноза. Точное совпадение фактических данных и прогностических точечных оценок, полученных путем экстраполяции кривых, характеризующих тенденцию, имеет малую вероятность.

Любой статистический прогноз носит приближенный характер. Поэтому целесообразно определение доверительных интервалов прогноза.

Точечный прогноз на k шагов вперед получается путем подстановки в модель параметра t=n+1, …, n+k. Доверительный интервал прогноза будет иметь следующие границы:

верхняя граница прогноза = y_p(n+k) + U(k),

нижняя граница прогноза = y_p(n+k) – U(k).

Величина U(k) для линейной модели имеет следующий вид:

где _y — средняя квадратическая ошибка тренда; y_p — расчетное значение уровня (по уравнению); m — число параметров уравнения (для линейного m = 2); n — количество исходных уровней; t — среднее значение параметра t (для имеющихся данных); k_p — доверительная величина, определяемая на основе t-критерия Стьюдента.

1. Средний абсолютный прирост находится по формуле:

где n — число периодов (уровней), включая базисный.

2. Средний темп роста вычисляется по формуле средней геометрической простой из цепных коэффициентов роста:

, .

Когда приходится производить расчет средних темпов роста по периодам различной продолжительности (неравноотстоящие уровни), то используют среднюю геометрическую, взвешенную по продолжительности периодов. Формула средней геометрической взвешенной будет иметь вид:

где t – интервал времени, в течение которого сохраняется данный темп роста.

3. Средний темп прироста не может быть определен непосредственно на основании последовательных темпов прироста или показателей среднего абсолютного прироста. Для его вычисления необходимо сначала найти средний темп роста, а затем его уменьшить на 100%:

4. Средний уровень интервального ряда находится по формуле средней арифметической простой, если интервалы равны, или по средней арифметической взвешенной, если интервалы не равны:

, .

где t - длительность интервала времени.

5. Средний уровень моментного ряда динамики так исчислить нельзя, так как отдельные уровни содержат элементы повторного счета.

а) Средний уровень моментного равноотстоящего ряда динамики находится по формуле средней хронологической:

.

где у₁ и у_n — значения уровней на начало и конец периода (квартала, года).

б) Средний уровень моментных рядов динамики с неравноотстоящими уровнями определяется по формуле средней хронологической взвешенной:

.

где t — длительность периода между смежными уровнями.

ЭКОНОМИЧЕСКИЕ ИНДЕКСЫ

В статистике под индексом понимается относительный показатель, который выражает соотношение величин какого-либо явления во времени, в пространстве или сравнение фактических данных с любым эталоном (план, прогноз, норматив и т. д.).