ПРЕДМЕТ, МЕТОД И ЗАДАЧИ СТАТИСТИКИ

Статистика как наука

это наука, разрабатывающая статистическую методологию т.е. набор приемов и способов сбора, обработки и анализа информации.

Предмет статистики

размеры и количественные соотношения качественно определенных социально-экономических явлений, закономерности их связи и развития в конкретных условиях места и времени.

Методы статистики

метод массовых наблюдений, метод группировок, методы анализа с помощью обобщающих показателей.

Основные этапы статистического исследования

Этап 1. Статистическое исследование начинается с формирования первичной статистической информационной базы по выбранному комплексу показателей.

Этап 2. Первичное обобщение и группировка статистических данных.

Этап 3. Следующий этап статистического исследования включает экономическую интерпретацию первичного обобщения.

Этап 4. Компьютерный анализ первичных и обобщенных расширенных (объемных) статистических данных.

Этап 5. Компьютерное прогнозирование по выбранным наиболее важным направлениям.

Этап 6. Обобщенный анализ полученных результатов и проверка их на достоверность по статистическим критериям

.Этап 7. Завершающим этапом статистического исследования является принятие управленческого решения.

Статистическая совокупность — это множество подвергающихся статистическому исследованию объектов или явлений, объединенных общими признаками, из которых один или несколько признаков не варьируют.

Единица совокупности — индивидуальный составной элемент статистической совокупности, являющийся носителем изучаемых признаков.

Признак, виды признаков

Признак — это объективная характеристика единицы статистической совокупности, характерная черта или свойство, которое может быть определено или измерено.

Признаки по форме выражения бывают количественные (дискретные и непрерывные) и качественные (атрибутивные, порядковые, альтернативные).

Вариация — изменчивость, многообразие значений (вариантов) признака.

Статистический показатель, их виды Статистический показатель представляет собой количественную характеристику социально-экономических явлений и процессов в условиях качественной определенности. В отличие от признака статистический показатель получается расчетным путем. Статистические показатели по форме выражения разделяются на абсолютные, относительные и средние. По временному фактору показатели бывают моментные (по состоянию на дату) и интервальные (за период).

Органы государственной статистики в РФ

Центральным органом государственной статистики является Федеральная служба государственной статистики РФ (Росстат). В регионах имеются территориальные органы Росстата.

СТАТИСТИЧЕСКОЕ ИЗМЕРЕНИЕ И НАБЛЮДЕНИЕ

Статистическое наблюдение – первый этап статистического исследования. Результат его является массив исходных данных об изучаемом объекте (первичная информация). Эта информация не публикуется.

Статистическое наблюдение — это научно организованный, планомерный и систематический процесс сбора массовых сведений о социально-экономических явлениях и процессах путем регистрации заранее намеченных существенных признаков.

Требования, предъявляемые к статистической информации— достоверность и сопоставимость данных.

Программно-методологические вопросы наблюдения — цели и задачи, объект, единицы наблюдения, единица совокупности, программа наблюдения, статистический формуляр и инструкции.

Организационные вопросы наблюдения — органы наблюдения, место и время проведения наблюдения, критический момент времени наблюдения, подготовка наблюдения и меры по обеспечению достоверности данных.

Виды наблюдения по охвату единиц совокупности — сплошное, несплошное (выборочное, основного массива, монографическое).

Виды наблюдения по временному фактору — текущее (непрерывное), периодическое и единовременное.

Виды наблюдения в зависимости о источника сведений — непосредственное, документальное, опрос.

Способы наблюдения — отчётный, экспедиционный, саморегистрации, анкетный, корреспондентский, явочный.

Ошибки наблюдения

Случайные ошибки – это ошибки, допущенные при заполнении бланков (цифра записана не в ту графу или допущена описка в записи), оговорка в ответах, нечеткость в вопросе и соответственно в ответе и т.д. Систематические ошибки могут быть преднамеренными и непреднамеренными. Преднамеренные ошибки(сознательные) получаются в результате того, что при знании действительного состояния (величины) признака сознательно сообщаются неправильные данные. Непреднамеренными называются ошибки, вызываемые случайными причинами: например, неправильностью измерительных приборов, невнимательностью регистраторов и др. Ошибки репрезентативности (представительности) свойственны не сплошному наблюдению. Они возникают в результате того, что состав отобранной для обследования части массового явления (части единиц совокупности, выборки) недостаточно полно отображает особенности, сущность всей изучаемой совокупности. Эти ошибки тоже могут быть случайными из-за того, что отобранные единицы совокупности неполно воспроизводят всю совокупность

СВОДКА И ГРУППИРОВКА

Статистическая сводка — это первичная обработка статистических данных с целью получения обобщенных характеристик изучаемого явления по ряду существенных для него признаков.

Статистическая группировка — это разбиение единиц изучаемой совокупности на качественно однородные группы по значениям одного или нескольких признаков.

Интервал – это значения количественного признака, лежащие в определенных границах. Интервал имеет свою длину (h), верхнюю и нижнюю границы (закрытые, например 30–50) или хотя бы одну из них (открытые, например до 50). По длине интервалы бывают равные и неравные.

Виды интервалов - открытые, закрытые, равные, неравные… Неравные делятся на прогрессивно возрастающие, прогрессивно убывающие, произвольные и специализированные. Неравные интервалы применяются в статистике, когда значения признака варьируют неравномерно и в значительных размерах, что характерно для большинства социально-экономических явлений, особенно при анализе макроэкономических показателей.

Если вариация признака является сравнительно небольшой, а распределение близко к равномерному, то строят группировку с равными интервалами.

Величина равного интервала определяется по формуле:

i = (Xmax — Xmin) / n

где  x max , x min – наибольшее и наименьшее значения группировочного признака в совокупности, n – число групп, x max – x min – размах вариации.

Полученную по формуле величину необходимо округлить. Она является шагом интервала.

Записывают     от 0 до 10;   от 10 до 20 и т.д. Или         0–10;   10–20

Открытые – это те интервалы, у которых указана только одна граница: верхняя – у первого интервала, нижняя – у последнего. Например, до 10, свыше 20. Ширина открытого интервала принимается равной ширине смежного с ним интервала.

Закрытыми называют интервалы, у которых обозначены обе границы.   0–10,   10–20

В общем случае при определении границ интервалов статистических группировок исходят из того, что изменение количественного признака приводит к появлению нового качества. Граница интервала устанавливается там, где происходит переход от одного качества к другому.

Формула Стерджеса

i = (Xmax — Xmin) / 1+ 3.322lg N

,где N –число единиц анализируемой совокупности

Виды группировок - типологическая, структурная, аналитическая; простая и комбинационная

Виды статистических группировок.

В зависимости от степени сложности массового явления и задач анализа - группировки могут производится по одному или нескольким признакам: Если производится группировка только по одному признаку, то она называется простой.

• Если по двум и более признакам, то такая группировка называется сложной или комбинационной.

^ В зависимости от решаемых задач различают типологические, структурные и аналитические группировки: Типологическая группировка — представляет собой разделение исследуемой совокупности на однородные группы. (группировка предприятий по формам собственности)

• Структурная группировка — группировка, в которой происходит разделение однородной совокупности на группы, характеризующие ее структуру по какому-то варьирующему признаку. (группировка населения по уровню дохода). Анализ статистических данных структурных группировок, взятых за ряд периодов показывает изменение структуры изучаемых явлений, то есть структурные сдвиги.

• ^ Аналитическая (факторная) группировка — позволяет выявить взаимосвязи между изучаемыми явлениями и их признаками. (группировка банков по сумме уставного капитала, величине активов и балансовой прибыли)

Вторичная группировка заключается в образовании новых групп на основе ранее произведенной группировки.

Группировочный признак - признак, принимаемый за основу образования групп в процессе статистической группировки. 

Определение числа интервалов, величины интервала (формулы)

Ряд распределения — представляет собой упорядоченное распределение единиц изучаемой совокупности на группы по определенному варьирующему признаку.

В зависимости от признака, положенного в основу образования ряда распределения различают атрибутивные и вариационные ряды распределения:

• Атрибутивными — называют ряды распределения, построенные по качественными признакам.

• Ряды распределения, построенные в порядке возрастания или убывания значений количественного признака называютсявариационными.

Частота, частость (формула) Частоты — это абсолютные числа, показывающие столько раз в совокупности встречается данное значение признака, которые обозначают   . Сумма всех частот равна должна быть равна численности единиц всей совокупности.

Частости (  ) — это частоты выраженные в процентах к итогу. Сумма всех частостей выраженных в процентах должна быть равна 100% в долях единице.

Плотность распределения (формула) Плотностью распределения вероятностей непрерывной случайной величины Х называется функция f(x) – первая производная от функции распределения F(x).

Полигон, гистограмма, кумулята, огива

Статистические таблицы — подлежащее, сказуемое, правила построения

Статистическая таблица - форма наиболее рационального изложения полученных в результате статистической сводки и группировки числовых (цифровых) данных По внешнему виду она представляет собой комбинацию вертикальных и горизонтальных строк, содержащую боковые и верхние заголовки. Статистическая таблица содержит подлежащее и сказуемое.

Подлежащее таблицы представляет ту статистическую совокупность, о которой идет речь в таблице, т. е. перечень отдельных или всех единиц сово­купности либо их групп. Чаще всего подлежащее помещается в левой части таблицы и содержит перечень строк.

Сказуемое таблицы - показатели, с помощью которых дается характеристика явления, отображаемого в таблице.

Если в подлежащем таблицы содержится простой перечень каких-либо объектов, таблица называется простой. В подлежащем простой таблицы нет ка­ких-либо группировок статистических данных. Если подлежащее простой таблицы содержит перечень территорий, то такая таблица называетсятерриториальной.

АБСОЛЮТНЫЕ И ОТНОСИТЕЛЬНЫЕ ВЕЛИЧИНЫ

Абсолютные величины Абсолютная величина – это показатель, выражающие размеры (объемы, уровни) социально-экономических явлений в единицах меры, веса, объема, протяженности, площади, стоимости и т.д. Абсолютные статистические величины — это числа именованные. Они всегда имеют определенную размерность, определенные единицы измерения.

Относительные величины Абсолютная величина – это показатель, выражающие размеры (объемы, уровни) социально-экономических явлений в единицах меры, веса, объема, протяженности, площади, стоимости и т.д. Абсолютные статистические величины — это числа именованные. Они всегда имеют определенную размерность, определенные единицы измерения.

Виды ОВ (формулы) Виды относительных величин:

1) относительная величина планового задания

ОВПЗ = Уплан₁ / Уфакт₀

2) относительная величина выполнения плана

ОВВП = Уфакт₁ / Уплан₁

3) относительная величина динамики

ОВД = У_i / У₀ =ОВПЗ · ОВВП

4) относительная величина структуры

ОВС = f_i / ∑f_i

5) относительная величина координации

ОВК = f_i / f_j

6) относительная величина сравнения

ОВСр = У_А / У_В

7) относительная величина интенсивности

ОВИ = У_А / Среда распространения У_А

Взаимосвязь ОВ

СРЕДНИЕ ВЕЛИЧИНЫ

Виды средних величин Виды средних величин:

1) Степенные (арифметическая, гармоническая, геометрическая, квадратическая и др.)

2) Структурные (мода, медиана, кварти́ли, деци́ли и др.).

ИСС (логическая формула)

ИСС =	Суммарное значение или объем осредняемого признака
	Число единиц или объем совокупности

Правила расчета средних Элементы степенной средней:

Варианта (х) — значения варьирующего количественного признака

Число единиц (n) — количество вариант в совокупности.

Веса (частоты f или частости ω) — показатели повторяемости вариант в совокупности.

Средняя арифметическая простая (невзвешенная) — эта форма средней используется в тех случаях, когда расчет осуществляется по несгруппированным данным

Средняя арифметическая взвешенная — эта форма средней используется в тех случаях, когда расчет осуществляется по сгруппированным данным и неизвестен числитель в логической формуле:

Средняя гармоническая взвешенная используется, когда известен числитель исходного соотношения средней, но неизвестен его знаменатель:

,

Средняя гармоническая невзвешенная (простая)

Средняя геометрическая невзвешенная:

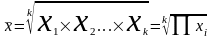
где k — количество осредняемых величин;

Средняя геометрическая взвешенная:

где f_i — вес i-гo варианта.

Средняя квадратическая невзвешенная

Средняя квадратическая взвешенная:

Структурные средние — мода и медиана Мода (Мо) представляет собой значение изучаемого признака, повторяющееся с наибольшей частотой. Моду можно определить для любого количественного и качественного признака. Мода отражает типичный, наиболее распространенный вариант значения признака.

Медианой (Me) называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности. Медиана делит ряд пополам, по обе стороны от нее находится одинаковое количество единиц совокупности. Медиану можно определить только для порядкового качественного признака. Медиана выполняет функции средней для неоднородной совокупности.

Расчет средних по дискретному вариационному ряду Определение моды по дискретному ряду распределения

Отыскиваем группу, в которой находится наибольшее число единиц (с максимальной частотой или частостью). Значение варианта признака (х) в этой группе и есть мода.

Для определения медианного значения признака находят номер медианной единицы ряда (№_Me):

где n — объем совокупности.

Определяют, в какой группе находятся единицы с этим порядковым номером. Для этого рассчитывают накопленные частоты (или частости). Значение варианта признака (х) в этой группе и есть медиана.

Расчет средних по интервальному вариационному ряду Определение моды и медианы по интервальным вариационным рядам

Определение моды и медианы требует проведения расчетов на основе следующих формул:

,

где х_o — нижняя граница модального интервала (модальным называется интервал, имеющий наибольшую частоту в случае равных интервалов); h — величина модального интервала; f_Mo — частота модального интервала; f_Mo-1 — частота интервала, предшествующего модальному; f_Mo+1 — частота интервала, следующего за модальным.

,

где х₀ — нижняя граница медианного интервала (медианным называется первый интервал, накопленная частота которого превышает половину общей суммы частот); h — величина медианного интервала; S_Мe-1 — накопленная частота интервала, предшествующего медианному; f_Me — частота медианного интервала.

ПОКАЗАТЕЛИ ВАРИАЦИИ

Вариация – это колеблемость, многообразие, изменяемость величины (вариантов) признака у отдельных единиц совокупности

Показатели вариации делятся на две группы: абсолютные и относительные.

К абсолютным относятся размах вариации, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение. Вторая группа показателей вычисляется как отношение абсолютных показателей вариации к средней арифметической (или медиане). Относительными показателями вариации являются коэффициенты осцилляции, вариации, относительное линейное отклонение и др.

Размах вариации (R) — это разность между наибольшим (x_max) и наименьшим (x_min) значениями варьирующего признака:

Среднее линейное отклонение ( ) — вычисляется как средняя арифметическая из абсолютных значений отклонений вариант x_i отx:

(простое);

(взвешенное)

Дисперсия (²) представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины и вычисляется по формулам простой и взвешенной дисперсий (в зависимости от исходных данных):

(простая);

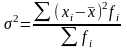(взвешенная)

Второй способ расчёта дисперсии:

_{где — средняя из квадратов индивидуальных значений}

Среднее квадратическое отклонение (стандартное отклонение) ():

Среднее квадратическое отклонение показывает, на какую величину в среднем значение признака отличается от среднего значения.

Исчисление среднего квадратического отклонения для явно несимметричных распределений не имеет смысла.

Относительные показатели вариации

Коэффициент осцилляции (V_R ):

Линейный коэффициент вариации ( ):

Коэффициент вариации (V_):

Наиболее часто в практических расчетах применяется коэффициент вариации. Совокупность считается однородной, если коэффициент вариации не превышает 33 % (для распределений, близких к нормальному).

Дисперсия альтернативного признака

Альтернативный признак – это признак, которым обладает часть единиц и не обладает другая часть единиц совокупности.

Дисперсия равна произведению доли (р) на дополняющее эту долю до единицы число (q):

.

где p – доля единиц, обладающих признаком;

q – доля единиц, не обладающих признаком.

Предельное значение дисперсии альтернативного признака равно 0,25 при р = 0,5.