2. Задача о коммивояжере

Постановка задачи:

Коммивояжер должен обойти n городов А₁, А₂, …, А_n. Расстояния, между которыми известны и заданы в матрице расстояний.

Коммивояжер должен побывать в каждом городе по одному разу. Необходимо построить маршрут, наименьшей протяженности проходящий через все города .

Алгоритм решения задачи:

Обозначим через t маршрут перемещения коммивояжера по городам i₁, i₂, …, i_n, : t= (i₁, i₂, …, i_n)

или t= {(i₁, i₂), (i₁, i₂), …, (i_n-1, i_n), (i_n, i₁)}

Длину маршрута t обозначим через l:

Рассмотрим расстояния от первого А1 города ко всем остальным:

c₁₂, c₁₃, …, c_1n.

Выберем из них минимальное:

h₁ =min(c₁₂, c₁₃, …, c_1n).

Аналогично можно для остальных строк матрицы найти такие же h_i. Так как маршрут должен выходить из каждого города, то величина

ω'= является нижней гранью длины маршрута, т.е. меньше этого расстояния коммивояжер не пройдет, каков его маршрут ни был.

Вычтем из каждой строки матрицы «свое» h_i (выполним приведение матрицы по строкам).

Здесь

c'_ij = c_ij - h_i или c_ij = c'_ij +h_i i=1,n, j=1,n.

В результате приведения матрицы, в каждой ее строке появится хотя бы один нуль.

Запишем длину маршрута :

l(t)=l(i₁, i₂, …, i_n )= = = + = + ω⁰,

здесь сумма по всем (i,j) є t (по парам городов, входящим в маршрут),

а ω⁰= .

ω= ω⁰+ = + .

Приведем матрицу по столбцам путем вычитания H_j из столбцов матрицы.

Здесь c "_ij = c'_ij - H _{j =} c_ij - h_i - H _j или c_ij = c"_ij + h_i + H _i i=1,n, j=1,n.

Длина маршрута t теперь может быть записана в виде

l(t)=l(i₁, i₂, …, i_n )= + ω.

В маршрут необходимо включать пары городов таким образом, чтобы была бы минимальной .

Пусть c"_pq =0. Непосредственный переход из города А_p в А_q, назовем «прямым»_, а переход из города А_p в А_q, через_, какой – то другой k-й город, назовем «окольным». Для каждой пары (p_,q), для которой c"_pq =0 оценим длину минимального окольного пути:

Θ(p_,q)= .

Для включения в маршрут выберем ту пару городов, для которой c" _k,m = 0 и

Θ(_k,m)=max Θ(p_,q).

Разобьем множество всех маршрутов (а их n!) на два подмножества Х и У. В Х отнесем все те маршруты, которые содержат прямой переход из А_k в А_m, обозначим это множество (k,m), а в У – все маршруты, которые не содержат прямого перехода из А_k в А_m, и обозначим его как (k,m). Тогда для множества У можно определить оценку, как

ξ(У) = ω + Θ(_k,m),

Построим теперь оценку для множества маршрутов Х. Для этого с"_m,k=∞, так как есть переход из А_k в А_m, то переход из А_m в А_k запрещаем. Так как А_k включен в маршрут (из него коммивояжер больше выходить не будет), то этот город необходимо исключить из рассмотрения, т.е. вычеркнем k-ю строку из матрицы. Аналогично исключаем m-й столбец матрицы (город А_m включен в маршрут и, следовательно, этот город не должен больше выбираться, как город, в который коммивояжер еще раз будет входить). При этом следует сохранять первоначальную нумерацию строк и столбцов матрицы.

Приведем снова матрицу по строкам и столбцам. Определим величину

ω'= '+ ',о которой можно сказать, что коммивояжер, в связи с включением в маршрут перехода (k,m), должен будет дополнительно к минимально необходимому пути пройти еще расстояние ω', т.е. оценка длины всех маршрутов, входящих в множество Х равна

ξ(Х) = ω + ω'.

Таким образом, дерево вариантов в этом случае примет вид:

ξ(G⁰)= ω ξ(Х)

ξ(У)

В этом дереве две вершины, выберем ту из них, у которой меньшая оценка. На первом шаге, вероятно, следует ожидать, что это будет вершина с множеством Х=(k,m). Дальше выполним снова ветвление выбранного множества на два подмножества, описанным выше способом . Этот процесс будет повторяться до тех пор, пока в матрице не останется две строки и два столбца, которые и завершат построение маршрута.

Пример решения задачи о коммивояжере:

Решение задачи:

	1	2	3	4	5	6	hi
1	-	41	60	39	46	10	10
2	31	-	59	16	1	51	1
3	29	51	-	14	42	50	14
4	32	12	52	-	16	26	12
5	16	39	15	60	-	57	15
6	15	30	38	47	36	-	15
Hj							67

	1	2	3	4	5	6	hi	αi
1	-	31	50	29	36	043	10	29
2	30	-	58	15	019	50	1	15
3	15	37	-	030	28	36	14	15
4	20	019	40	-	4	14	12	4
5	1	24	019	45	-	42	15	1
6	016	15	18	32	21	-	15	15
Hj	0	0	0	0	0	0	67
βj	1	15	18	15	4	14

	1	2	3	4	5	hi	αi
2	30	-	58	15	0	0
3	15	37	-	0	28	0
4	20	0	40	-	4	0
5	1	24	0	45	-	0
6	0	15	18	32	21	15
Hj
βj

	1	2	3	4	5	hi	αi
2	30	-	58	15	0	0
3	15	37	-	0	28	0
4	20	0	40	-	4	0
5	1	24	0	45	-	0
6	0	0	3	17	6	15
Hj	1	0	0	0	0	16
βj

	1	2	3	4	5	hi	αi
2	29	-	58	15	0­19		15
3	14	37	-	029	28		14
4	29	0­0	58	-	4		0
5	014	24	03	45	-		0
6	0	03	3	17	6		3
Hj
βj	14	0	3	15	4

	1	2	3	5	hi	αi
2	29	-	58	031	0	29
4	29	025	58	4	0	25
5	029	24	03	-	0	0
6	0	03	3	6	0	3
Hj	0	0	0	0	0
βj	29	0	3	4

	1	2	3	hi	αi
4	25	025	58	0	25
5	025	24	03	0	0
6	0	03	3	0	3
Hj	0	0	0	0
βj	25	0	3

	1	3	hi	αi
5	0	0	0
6	0	3	0
Hj	0	0	0
βj

О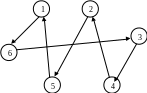 твет:

L=83 Путь: 1-6-3-4-2-5-1