С.Ж.АСФЕНДИЯРОВ АТЫНДАҒЫ ҚАЗАҚ ҰЛТТЫҚ МЕДИЦИНА УНИВЕРСИТЕТІ |
|
КАЗАХСКИЙ НАЦИОНАЛЬНЫЙ МЕДИЦИНСКИЙ УНИВЕРСИТЕТ ИМЕНИ С.Д.АСФЕНДИЯРОВА |
МОДУЛЬ МЕДИЦИНСКОЙ БИОФИЗИКИ И БИОСТАТИСТИКИ ЭКЗАМЕНАЦИОННЫЕ ТЕСТОВЫЕ ВОПРОСЫ |
||
«Согласовано» Председатель КОП Суатай С.К. _______ «___»_______2013г. |
«Утверждаю» И.о. директора УДОД Сарыбаев М.С. _______ «___»_______2013г. |
Экзаменационные тестовые вопросы по дисциплине «Математика» для студентов 2-го курса, обучающихся по специальности 051102 – «Общественное здравоохранение»
1. А и В события, связанные одним и тем же испытанием. Покажите событие, означающее наступление события А или В:
1. А/В.
2. А*В.
3.+ А+В.
4. (А/В)+(В/А)
5. (А/В)*(В/А).
2. Событие А - хотя бы один из четырех обследуемых болен. Что означает противоположное событие:
1.
+
– все обследуемые здоровы.
2. – болен один или не более одного.
3. – все обследуемые больны.
4. – трое обследуемых здоровы.
5. – трое обследуемых больны.
3. Из колоды в 52 карты наудачу взята одна карта. Вероятность того, что она окажется тузом равна:
1. 1.
2. ½
3. +1/13.
4. 1/26.
5. 1/3.
4. Из колоды в 52 карты наудачу взята одна карта. Вероятность того, что эта карта будет черного цвета масти равна:
1. 1.
2.+ ½
3. 1/13.
4. 1/26.
5. 1/3.
5. Из слова "студент" случайным образом выбирают букву. Какова вероятность, что выбранной окажется гласная буква:
1.+ 2/7.
2. 1/7.
3. 7/2.
4. 1/3.
5. 2/3.
6. Обследовано 100 человек, причем зарегистрировано 20 больных ОРВИ. Относительная частота встречаемости этого заболевания равна:
1. 1.
2. 2.
3. 0,5.
4. 0,02.
5. +0,2.
7. Два несовместных события, составляющие полную группу:
1. Несовместные.
2. Совместные.
3. +Противоположные.
4. Достоверные
5. Невозможные.
8. Событие А называется независимым от события В, если:
1. Они несовместны.
2. +Вероятность события А не зависит от того, произошло событие В или нет.
3. Вероятность события А вычисляется при условии выполнения события В.
4. Имеет место событие С.
5. Вероятность события А зависит от того, произошло событие В или нет.
9. Пространством элементарных событий называется
1. Множество всех невозможных элементарных событий.
2. Совместные элементарные событии
3.+ Множество всех возможных элементарных событий.
4. Несовместные элементарные события
5. Множество невозможных событий.
10. Событие А называется зависимым от события В, если...
1. Они несовместны.
2. Вероятность события А не зависит от того, произошло событие В или нет.
3. Вероятность события А вычисляется при условии выполнения события В.
4. Имеет место событие С.
5.+ Вероятность события А зависит от того, произошло событие В или нет.
11. Стрелок стреляет по мишени, разделенной на 3 области. Вероятность попадания в первую область равна 0,15, во вторую – 0,45. Найти вероятность того, что стрелок при одном выстреле попадет либо в первую, либо во вторую область.
1. p=0,5.
2. p=0,1.
3. p=0,7.
4.+ p=0,6.
5. p=0,2.
12. Укажите интегральную формулу Лапласа:
1.
.
2.
.
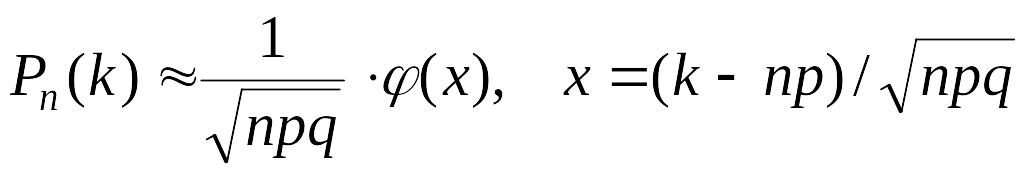3.
+
.
4.
.
5.
.
13. Случайным событием называется всякое явление, которое ..., при осуществлении определенных совокупностей условий:
1. может произойти
2. может не произойти
3. + может произойти или не произойти
4. никогда не произойдет
5. которое обязательно произойдет
14. Событие, неизбежно происходящее при испытании, называется:
1. Случайным
2. Невозможным
3. Совместным
4.+ Достоверным
5. комплексом условий
15. Случайные события несовместны:
1. если событие А и В наступают одновременно
2. если появление одного события не имеет какого-либо преимущества перед появлением другого
3. если наступление события В влечет за собой наступление события А
4. если нет никаких объективных причин считать, что одно из них наступает чаще, чем другое
5.+ если в результате испытания появление одного события исключает возможность появления другого события
16.
Пусть случайное событие А имело место
NA
раз после одинаковых испытаний. Отношение
называется:
1. вероятностью события А
2. статистической устойчивостью
3. +относительной частотой события А
4. совместным событием
5. невозможным событием А
17. Вероятностью события А называют...
1. +Отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу.
2. Предел произведения вероятности одного из них на условную вероятность другого.
3. Cумма вероятностей события В.
4. Сумма вероятностей невозможных событий
5. Событие которое обязательно наступит.
18. Вероятность любого события
1.
.
2.
+
.
3.
.
4.
.
5.
.
19. Самую большую вероятность равную 1, имеет событие ...
1. Невозможное событие.
2. Случайное событие.
3. +Достоверное событие.
4. Возможноe событие.
5. Совместным событием.
20. Наименьшая вероятность, равная 0, у ... события.
1. +Невозможного
2. Случайного
3. Достоверного
4. Возможного
5. Возможного
21. Вероятность совместного появления независимых событий равна:
1. Сумме вероятностей этих событий.
2. Произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие имеет место.
3. +Произведению вероятностей этих событий.
4. Вероятности события В.
5. Вероятности события А
22. Вероятность совместного появления зависимых событий равна
1. Сумме вероятностей этих событий, вычисленных в предположении, что первое событие имеет место.
2.+ Произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие имеет место.
3. произведению вероятностей этих событий.
4. Вероятности события B.
5. Вероятности события A.
23. Вероятность поступления хотя бы одного вызова врача в течение часа Р(А)=0, 85. Найдите вероятность того, что в течение часа не последует вызовов.
1. 1.
2. 0,7.
3. 0,85.
4. +0,15.
5. 1,5.
24. По мишени сделано 4 выстрела. Вероятность попадания в цель 0, 25. Укажите формулу вычисления вероятности попадания в цель.
1.
2.
3.
4. P(AВ)= P(А) PA(В)
5.
+
25. Результат испытания, который нельзя заранее прогнозировать, называется...
1. +случайным событием
2. Событием
3. достоверным событием
4. невозможным событием
5. Комплексом условий.
26. Совмещением двух событии А и В называется событие, состоящее в том, что
1. произойдет по крайней мере одно из событий А или В
2. появление события А исключит появление события В
3. + наступят одновременно события В и А
4. одно из них может появляться чаще чем другое
5. появление одного события не имеет какого-либо преимущества перед появлением другого
27. Игральная кость брошена на твердую горизонтальную поверхность. Найти вероятность того, что выпадет число кратное 3.
1. 0.
2. 1.
3. +1/3.
4. 0,7.
5. 0,6.
28. Формула вычисления относительной частоты
1.
2.
3.
PB(А)=
4.
5.
+
29. Вероятность рождения мальчика в семье 0, 515. Какова вероятность рождения девочки?
1. p=0,785.
2. +p=0,485.
3. p=0,848.
4. p=0,668.
5. p=0,585.
30. Вероятность совместного появления двух зависимых событий равна:
1.
2.
3.
P(1.+
=1
4.
5. +P(AВ)=P(А)PA(В)
31. Вероятность появления одного из двух несовместных событий равна:
1. +
2.
3.
P(А)+
=1
4.
5. P(AВ)=P(А)PA(В)
32. Сумма вероятностей противоположных событий равна:
1.
2.
3. +P(А)+ =1
4.
5. P(AВ)=P(А)PA(В)
33. В коробке находятся 3 черных, 5 белых, 4 красных шара. Какова вероятность того, что наудачу выбранный шар будет красным?
1. 0,25.
2. +1/3.
3. 2/3.
4. 5/12.
5. 1.
34. Пусть брошены 2 монеты. Какова вероятность появления герба и цифры?
1. 0.
2. +1/4.
3. 1/3.
4. 0,5.
5. 1.
35. Пусть брошены 2 монеты. Какова вероятность появления двух гербов?
1. 1/8.
2. 1/9.
3. +1/4
4. 1/5.
5. 1.
36. Пусть брошены 2 монеты. Какова вероятность появления двух цифр?
1. 1/8.
2. 1/9.
3.+1/4
4. 1/5.
5. 1.
37. В ящике находятся 10 шаров: из них 4 черных, 6 белых. Какова вероятность того, что наудачу выбранные 2 шара будут белые?
1. 1/7.
2. +1/3.
3. 0,25.
4. 1/5.
5. 1
38. Формула Бернулли:
1.
.
2.
+
.
3.
.
4.
.
5.
.
39. Если событие А наступает с вероятностью 0, 25 в 5 испытаниях, то какое выражение определит вероятность наступления данного события 2 раза:
1.
2.
+
3.
4.
5.
40. Вероятность случайного события
1. .
2.
+
.
3. 0.
4. 1.
5. .
41. Вероятность совместного появления независимых событий
1. +P(A*В)=P(А)*P(В).
2. P(A+В)=P(А)+P(В).
3. P(A-В)=P(А)*P(В) - P(А).
4. P(A-В)=P(А)*P(В) - P(В).
5. P(A*В)=P(А)*P(В) - P(A*В).