5.2 Результаты повторного эксперимента, проведенного не в полном объеме

Результаты повторного эксперимента представим в виде таблицы (результаты повторного эксперимента представлены в таблице 8).

Таблица 8 – План и результаты повторного эксперимента

Оператор,	СИ,	Смена,	Измеренное значение
1	2	3	5
1	1	1	29,946
		2	29,948
	2	1	29,944
		2	29,949
2	1	1	29,945
		2	29,947
	2	1	29,947
		2	29,943

Полученные результаты должны быть обработаны в соответствии с СТБ ИСО 5725-3.

5.2.1 Проверка на наличие выбросов в пределах каждого опыта

Проверка на наличие выбросов не проводится, поскольку в пределах каждого опыта осуществляется лишь одно измерение.

5.2.2 Проверка на нормальность распределения

Проверка на нормальность распределения результатов измерений не проводится, поскольку в пределах каждого опыта осуществляется лишь одно измерение.

5.2.3 Оценивание вклада лабораторной составляющей

Проведем трехфакторный дисперсионный анализ без повторных измерений. Воспользуемся возможностями пакета Statistica. Для этого составим план эксперимента в программе (план эксперимента в пакете статистика представлен на рисунке 3).

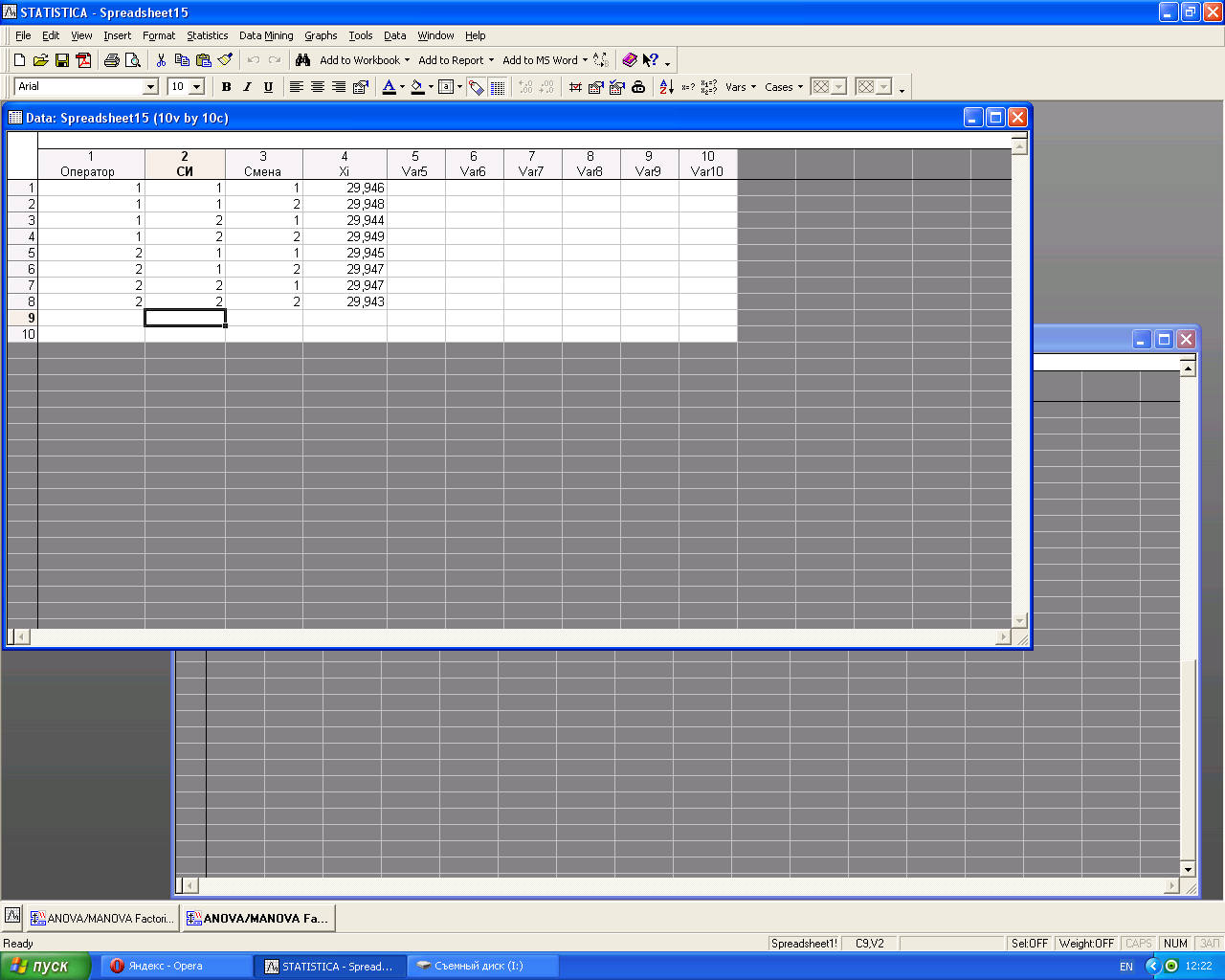
Рисунок 3 – План повторного эксперимента

Результаты дисперсионного анализа представим в виде таблицы (результаты дисперсионного анализа представлены в таблице 9).

Таблица 9 – Результаты дисперсионного анализа

Источник изменчивости,	Сумма квадратов эффектов,	Число степеней свободы,	Средние квадраты,
Оператор	0,00014		0,00007
СИ	0,00013		0,000065
Смена	0,00011		0,000055
Оператор*СИ	0,000012		0,000012
Оператор*смена	0,000012		0,000012
СИ*смена	0,000012		0,000012
Оператор*СИ*смена	0,000001		0,000001
Случайная ошибка	0,00028		0,00035

Выдвигаем гипотезу об отсутствии влияния на результат измерений рассматриваемых источников изменчивости. Полученные значения критерия Фишера представим в виде таблицы (рассчитанные значения критерия Фишера для каждого источника изменчивости представлены в таблице 10).

Таблица 10 – Рассчитанные значения критерия Фишера

Источник изменчивости,	Средние квадраты,	Критерий Фишера,
Оператор	0,00007	0,2
СИ	0,000065	0,185714
Смена	0,000055	0,157143
Оператор*СИ	0,000012	0,034286
Оператор*смена	0,000012	0,034286
СИ*смена	0,000012	0,034286
Оператор*СИ*смена	0,000001	0,002857
Случайная ошибка	0,00035

Проанализировав таблицу 10 можно селать вывод, что гипотеза об отсутствии влияния на результат измерений всех источников изменчивости принимается в связи с тем, что рассчитанные значения критерия Фишера не превосходят табличного значения данного критерия.

Таким образом, на основании проведенных расчетов можно сделать вывод, что система измерения находится в стабильном состоянии и обладает достаточной точностью, что позволяет использовать данную систему измерения для построения карт контроля качества, чтобы оценить пригодность технологического процесса.