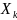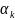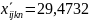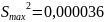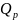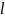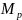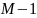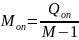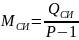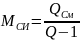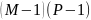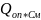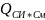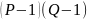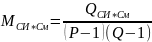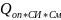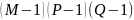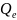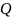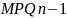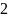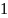- •«Полный анализ системы измерения»
- •1 Предпосылки проведения полного анализы системы измерения
- •2 Реализация первого этапа полного анализа системы измерений
- •2.1 Постановка задачи
- •2.2 План эксперимента
- •2.3 Результаты эксперимента
- •3 Реализация второго этапа полного анализа системы измерений
- •3.1 Модель измерения
- •3.2 Обработка данных, полученных в результате проведения измерительного эксперимента
- •4 Реализация третьего этапа полного анализа системы измерений
- •5 Реализация четвертого этапа полного анализа системы измерений
- •5.1 Разработка плана корректирующих мероприятий
- •5.2 Результаты повторного эксперимента, проведенного не в полном объеме
3 Реализация второго этапа полного анализа системы измерений
3.1 Модель измерения
СТБ ИСО 5725-3 предлагает следующую модель результата измерений:

где
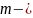 общее
среднее значение (математическое
ожидание);
общее
среднее значение (математическое
ожидание);
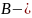 лабораторная
составляющая смещения согласно условиям
повторяемости;
лабораторная
составляющая смещения согласно условиям
повторяемости;
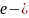 случайная
погрешность, имеющая место при каждом
измерении согласно условиям повторяемости.
случайная
погрешность, имеющая место при каждом
измерении согласно условиям повторяемости.
Общее
среднее значение
это
общее среднее арифметическое всех
результатов измерений. Значение
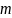 зависит исключительно от «истинного
значения» и метода измерений и не зависит
от оборудования, оператора или времени,
за которое был получен результат
измерений. Поэтому данная составляющая
результата измерения не рассматривается
при решении поставленной задачи.
зависит исключительно от «истинного
значения» и метода измерений и не зависит
от оборудования, оператора или времени,
за которое был получен результат
измерений. Поэтому данная составляющая
результата измерения не рассматривается
при решении поставленной задачи.
Лабораторная
составляющая
 представляет собой отклонение лаборатории
от
по той или иной причине безотносительно
к случайной погрешности
представляет собой отклонение лаборатории
от
по той или иной причине безотносительно
к случайной погрешности
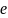 ,
имеющей место в каждом результате
измерений. Однако очевидно, что в общем
значении члена
воплощены эффекты, которые вызваны,
сменой оборудования, оператора и времени,
в течении которого проводятся измерения,
поэтому статистическую модель можно
переписать в форме:
,
имеющей место в каждом результате
измерений. Однако очевидно, что в общем
значении члена
воплощены эффекты, которые вызваны,
сменой оборудования, оператора и времени,
в течении которого проводятся измерения,
поэтому статистическую модель можно
переписать в форме:

где
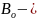 вклад из-за смены оператора;
вклад из-за смены оператора;
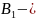 вклад
из-за смены применяемого средства;
вклад
из-за смены применяемого средства;
 вклад
из-за смены времени, в течении которого
проводятся измерения (смена).
вклад
из-за смены времени, в течении которого
проводятся измерения (смена).
Составляющая представляет собой случайную погрешность, встречающуюся в каждом результате измерений.
Таким образом, исходя из поставленной задачи, для нас представляет интерес составляющие результата каждого измерения , оценивание вкладов которых осуществляется на основании данных измерительного эксперимента, результаты которого представлены в таблице 1.
3.2 Обработка данных, полученных в результате проведения измерительного эксперимента
3.2.1 Проверка на наличие выбросов в пределах каждого опыта
Прежде чем приступать к дисперсионному анализу, необходимо обработать результаты измерений при каждом опыте.
Для
проверки наличия статистических выбросов
среди результатов измерений, полученных
в условиях каждого из
опытов для
выборок малых объемов, воспользуемся
критерий
Романовского
 в отношении подозрительных результатов
измерений.
в отношении подозрительных результатов
измерений.
Подозрение вызывает только два результата измерений:
опыты, проведенные оператором 2 с использованием первого СИ за вторую смену – 29,934;
опыты, проведенные оператором 2 с использованием второго СИ во вторую смену – 29,965.
Определим среднее значение результата измерения в пределах каждого опыта с подозрительным результатом:

Тогда для шестого и восьмого опытов среднее значение результатов измерений равно:

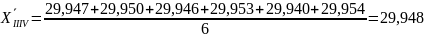
Стандартное отклонение результатов измерений в пределах каждого опыта с подозрительными результатами определяется по формуле:
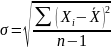
Тогда для шестого и восьмого опытов стандартное отклонение результатов измерений равно:
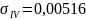
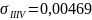
Примечание
– Расчет
 и
и
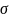 осуществляется без учета подозрительного
значения.
осуществляется без учета подозрительного
значения.
Рассчитаем критерий Романовского для шестого и восьмого опытов:


Из
таблицы для
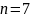 выбираем табличное значение критерия:
выбираем табличное значение критерия:
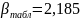
Поскольку
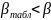 ,
то результаты не являются промахами.
,
то результаты не являются промахами.
3.2.2 Проверка на нормальность распределения
Из известных критериев согласия имеет место критерий Шапиро-Уилка, который используется при проверке распределения на нормальность для выборок малых объемов (не превосходящих 20), который определяется по формуле:
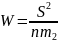


где
 индекс, имеющий значения от 1 до
индекс, имеющий значения от 1 до
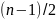 ;
;
 коэффициент,
имеющий специальные значения для объема
выборки
коэффициент,
имеющий специальные значения для объема
выборки
Таблица 2 – Результаты промежуточных расчетов в пределах первого опыта
|
|
|
29,949 |
29,947 |
0,605 |
29,945 |
29,945 |
0,316 |
29,934 |
29,943 |
0,174 |
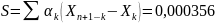
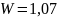
Табличное значение критерия равно 0,818. Поскольку табличное значение не превосходит рассчитанное, то гипотеза о нормальном распределении принимается.
Аналогичным образом осуществляется проверка для остальных семи опытов. И поскольку табличное значение критерия не превосходит рассчитанные значения, то гипотеза о нормальном распределении результатов измерений в пределах каждого опыта принимается.
3.2.3 Проверка на однородность дисперсий
Если в процессе проведения измерительного эксперимента использовались различное СИ, измерения выполняли различные операторы, а также измерения выполнялись в разные смены, то необходимо убедиться, что дисперсии однородны
Проверка однородности дисперсий осуществляется с помощью критерия Кохрана:

где
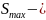 наибольшее стандартное отклонение в
совокупности;
наибольшее стандартное отклонение в
совокупности;
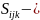 стандартное
отклонение в пределах каждого из 8-ми
опытов.
стандартное
отклонение в пределах каждого из 8-ми
опытов.
Представим результаты промежуточных расчетов для определения критерия в таблице (результаты промежуточных расчетов представлены в таблице 3).
Таблица 3 – Результаты промежуточных расчетов
Оператор |
СИ |
Смена |
|
|
1 |
1 |
1 |
29,9435 |
0,000023 |
1 |
1 |
2 |
29,9481 |
0,000019 |
1 |
2 |
1 |
29,9481 |
0,000030 |
1 |
2 |
2 |
29,9502 |
0,000036 |
2 |
1 |
1 |
29,9481 |
0,000035 |
2 |
1 |
2 |
29,9478 |
0,000033 |
2 |
2 |
1 |
29,9448 |
0,000022 |
2 |
2 |
2 |
29,9475 |
0,000029 |
|
|
|
|
|
Таким образом, критерий Кохрена определяется:
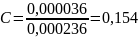
Критическое значение 0,3362. Поскольку критическое значение критерия больше рассчитанного, то дисперсии, полученные в пределах каждого опыта однородны.
Критерий Фишера для определения однородности дисперсий используется для опытов с различным количеством измерений.
3.2.4 Оценивание вклада лабораторной составляющей
Для исследования влияния всех уровней факторов на результаты измерений используется дисперсионный анализ. Поскольку измерения проводят в промежуточных условиях прецизионности с тремя изменяющимися факторами, то проведем трехфакторный дисперсионный анализ.
Трехфакторный дичперсионный анализ проведем, используя пакет Statistica. Для этого составим план эксперимента в программе (план эксперимента в пакете статистика представлен на рисунке 2).
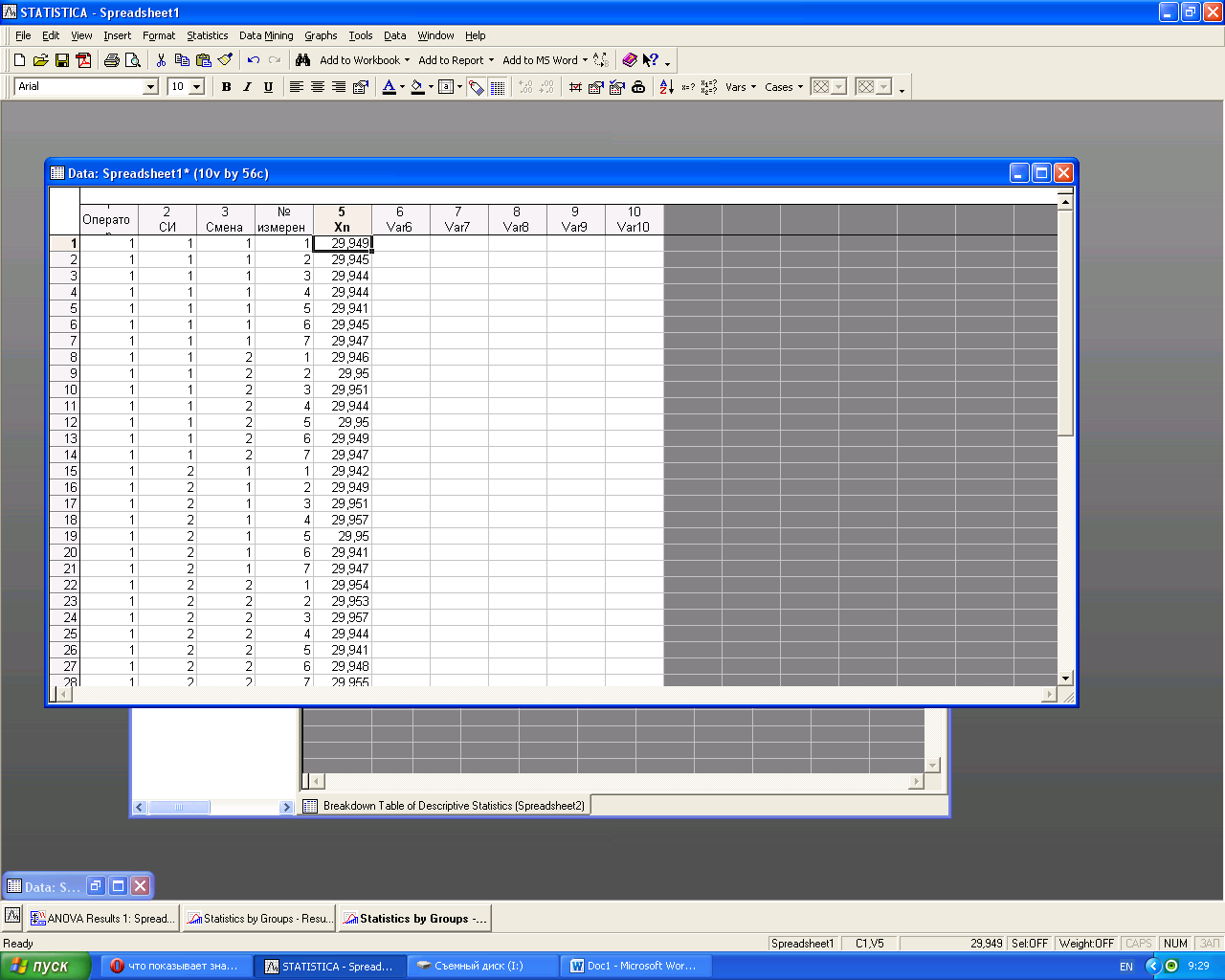
Рисунок 2 – План эксперимента
Проведем
трехфакторный дисперсионный анализ
для определения вкладов от каждой
составляющей
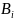 ,
их попарного и тройного взаимодействия
и результаты представи в виде таблица
4.
,
их попарного и тройного взаимодействия
и результаты представи в виде таблица
4.
Таблица 4 – Итоговая таблица результатов дисперсионного анализа
Источник изменчивости,
|
Сумма квадратов эффектов,
|
Число степеней свободы,
|
Средние квадраты,
|
Оператор |
|
|
|
СИ |
|
|
|
Смена |
|
|
|
Оператор*СИ |
|
|
|
Оператор*смена |
|
|
|
СИ*смена |
|
|
|
Оператор*СИ *смена |
|
|
|
Случайная ошибка |
|
|
|
Общая |
|
|
|
Дисперсионный анализ позволяет определить какой вклад вносит каждый изменяющийся фактор измерительной системы: оператор, СИ и смена – а также оценить вклады от взаимодействия этих факторов (результаты дисперсионного анализа представлены в таблице 5).
Таблица 5 – Результаты дисперсионного анализа
Источник изменчивости,
|
Сумма квадратов эффектов,
|
Число степеней свободы,
|
Средние квадраты,
|
Оператор |
0,01028 |
|
0,00514 |
СИ |
0,0023 |
|
0,00115 |
Смена |
0,0024 |
|
0,00120 |
Оператор*СИ |
0,000252 |
|
0,000252 |
Оператор*смена |
0,000071 |
|
0,000071 |
СИ*смена |
0,00011 |
|
0,00011 |
Оператор*СИ*смена |
0,000178 |
|
0,000178 |
Случайная ошибка |
0,006608 |
|
0,000826 |