
- •«Валидация и верификация методик (методов) измерений» Внутрилабораторные исследования
- •1 Основные понятия и определения
- •1.1 Понятие валидации
- •1.2 Понятие верификации
- •2 Показатели, определяемые при валидации и верификации
- •3 Разница между валидацией и верификацией
- •Технические нормативные правовые акты
- •Приложение а
- •Внутрилабораторное исследование по оценке характеристик точности метода измерений теплопроводности
Приложение а
(справочное)
Внутрилабораторное исследование по оценке характеристик точности метода измерений теплопроводности
Задача: Измерительная лаборатория хочет аккредитоваться на право проведения измерений теплопроводности, для этого необходимо: провести внутрилабораторное исследование по оценке характеристик точности метода измерений теплопроводности, основной целью которого является определение характеристик верификации метода (промежуточная прецизионность, смещение), а также определить какая из составляющих измерения теплопроводности вносит наибольший вклад в неопределенность.
Решение:
Существует документ, определяющий метод измерения теплопроводности: ГОСТ 7076-99 «Материалы и изделия строительные. Метод определения теплопроводности и термического сопротивления при стационарном тепловом режиме». В соответствии с этим документом подбираем прибор для измерения теплопроводности, соответствующий требованию стандарта, а именно:
- прибор, собранный по симметричной схеме, оснащенный двумя тепломерами, один из которых расположен между испытываемым образцом и холодной плитой прибора, а второй – между образцом и горячей плитой прибора.
Исходя из данного требования выбираем следующий прибор:
Измеритель теплового потока HFM 436 – прибор для измерения материалов с низкими значениями теплопроводности, например, изоляционных. Прибор HFM 436 (рисунок А.1) работает в соответствии с методом, изложенным в ГОСТ 7076-99.

Рисунок А.1 – Измеритель теплового потока HFM 436
Основные технические характеристики прибора HFM 436 представлены в таблице А.1.
Таблица А.1 – Основные технические характеристики прибора HFM 436
Техническая характеристика |
Значение |
Диапазон воспроизводимых температур, С |
от минус 30 до плюс 90 |
Диапазон воспроизводимой/измеряемой разности температур, С |
от 10 до 30 |
Пределы абсолютной погрешности воспроизведения/измерения разности температуры, С |
0,5 |
Абсолютная погрешность измерения расстояний, мм |
0,5 |
Диапазон измерения теплопроводности, Вт/(м·K) |
от 0,005 до 0,50 |
Пределы допускаемой относительной погрешности измерения теплопроводности, % |
от 1,0 до 3,0 |
Условия эксплуатации: – температура окружающего воздуха, °С – относительная влажность воздуха, % – атмосферное давление, кПа |
235 65±15 от 86 до 104 |
Номинальное напряжение питания переменного тока, В |
230 |
Номинальная частота переменного тока, Гц |
50 |
Габаритные размеры, мм, не более |
486351 |
Для измерения температуры окружающего воздуха и относительной влажности используется психрометр ПБУ-1 с диапазоном измерения влажности от 40 до 80 % и диапазоном измерения сухого термометра от 0 до + 40 °С, с ценой деления 0,2 °С, пределом допускаемой погрешности ± 1,5 %.
Для измерения атмосферного давления используется барометр-анероид БАММ-1, предназначенный для измерения атмосферного давления в наземных условиях при температуре от 0 до + 40 °C и относительной влажности воздуха до 80 %, с диапазоном измеряемого давления 80 – 106 кПа, ценой деления 0,1 кПа, пределом допускаемой основной погрешности ± 0,2 кПа и дополнительной погрешности ± 0,5 кПа.
Образец помещают в прибор между двумя плитами с различной температурой. Тепловой поток через образец измеряется (калиброванным) датчиком теплового потока. Измерения выполняются после установки стационарного теплового режима. Для анализа используется только центральная часть образца.
Прибор HFM 436 поставляется со встроенным датчиком измерения длины и позволяет определять текущую толщину образца автоматически во время измерения.
Схема прибора HFM 436 представлена на рисунке А.2.

Рисунок А.2 – Схема прибора HFM 436
Средняя температура и разность температур между плитами задаются пользователем с панели прибора. Измерение разности температур в образце осуществляется с помощью термопар, встроенных в поверхности плит. Температуры каждой плиты регулируются системами Пельтье.
Система Пельтье конструктивно состоит из последовательного соединения множества чередующихся полупроводниковых элементов p-типа и n-типа. При протекании постоянного тока через такое соединение одна часть p-n контактов нагревается, другая наоборот – охлаждается. Полупроводниковые элементы ориентированы так, чтобы греющиеся контакты были на одной стороне, а охлаждающиеся – на другой. Охлаждение/нагревание систем Пельтье осуществляется путем использования встроенной жидкостной циркуляции. Нагретая жидкость охлаждается вновь с помощью встроенной системы охлаждения сжатым воздухом.
На рабочих поверхностях каждой плиты смонтированы датчики теплового потока. Датчики теплового потока измеряют напряжение, которое пропорционально тепловому потоку, проходящему через образец. На тепловое равновесие указывают установившиеся значения термопар и датчиков теплового потока. По достижении теплового равновесия показания регистрируются и начинается следующее измерение при новых значениях температур.
Теплопроводность рассчитывается по формуле:

где
 – коэффициент калибровки, показывающий
отношение сигнала датчика теплового
потока (в В) к тепловому потоку через
образец;
– коэффициент калибровки, показывающий
отношение сигнала датчика теплового
потока (в В) к тепловому потоку через
образец;
 – сигнал
датчика теплового потока, В;
– сигнал
датчика теплового потока, В;
 – толщина
образца, м;
– толщина
образца, м;
 – разность
температуры в образце, К.
– разность
температуры в образце, К.
Прибор HFM 436 имеет встроенный микропроцессор и работающий под управлением внутреннего программного пакета Q-Test. Программы измерений могут задаваться прямо с панели прибора, а результаты измерений выводятся на печать в виде таблицы А.2.
Таблица А.2 – Форма представления результатов измерений теплопроводности
х, м |
Tв, С |
Tн, С |
Tср, С |
T, С |
Qв, мкВ |
Qн, мкВ |
N(t) |
λ(t), Вт/(м·К) |
Status |
|
|
|
|
|
|
|
|
|
|
В данной таблице:
х – толщина измеряемого образца, м;
Тв – температура верхней плиты, C;
Tн – температура нижней плиты, C;
Tср – среднее значение температуры, вычисленное из температуры верхней (Тв) и нижней (Tн) плит, C;
T – разница между температурами верхней (Тв) и нижней (Tн) плит, C;
Qв– сигнал верхнего датчика теплового потока, мкВ;
Qн – сигнал нижнего датчика теплового потока, мкВ;
N(t) – коэффициент калибровки датчика теплового потока при температуре t, который показывает отношение сигнала датчика теплового потока в вольтах к тепловому потоку через образец;
λ(t) – теплопроводность при соответствующем значении температуры образца, Вт/(м·К).
Отбор образцов:
Отбор образцов осуществляется в соответствии с ГОСТ 7076-99 «Материалы и изделия строительные. Метод определения теплопроводности и термического сопротивления при стационарном тепловом режиме».
Согласно данному стандарту: число образцов, необходимое для определения теплопроводности, и порядок отбора образцов должны быть указаны в стандарте на конкретный материал или изделие.
Для измерительного эксперимента в рассматриваемом исследовании были выбраны образцы теплоизоляционных материалов с различными значениями теплопроводности: минеральная вата и пенополистирол.
Минеральная вата по ГОСТ 9573-96 «Плиты из минеральной ваты на синтетическом связующем теплоизоляционные. Технические условия» (рисунок А.3) – это теплоизоляционный материал, состоящий из тончайших стекловидных волокон, получаемый из минерального сырья (базальта, доломита и т.д.).

Рисунок А.3 – Минеральная вата
Изготавливают 2 образца, по одному из каждой плиты попавшей в выборку, в виде прямоугольного параллелепипеда, размер образца определяется в соответствии с размером рабочей поверхности плиты прибора 30,030,0 мм, толщина образцов 30 мм и 50 мм (измерения проводились при номинальных средних температурах поверхностей образцов 10 С и 25 С).
В соответствии с разделом 6 ГОСТ 9573-96 теплопроводность определяют по ГОСТ 7076-99.
Пенополистирол по ГОСТ 15588-86 «Плиты пенополистирольные. Технические условия» (рисунок А.4) — лёгкий газонаполненный материал класса пенопластмасс на основе полистирола или его производных.

Рисунок А.4 – Пенополистирол
Изготавливают 2 образца, по одному из каждой плиты попавшей в выборку, в виде прямоугольного параллелепипеда, размер образца определяется в соответствии с размером рабочей поверхности плиты прибора 30,030,0 мм, толщина образцов 30 мм и 50 мм (измерения проводились при номинальных средних температурах поверхностей образцов 10 С и 25 С).
В соответствии с разделом 4 ГОСТ 15588 теплопроводность для пенополистирола определяют по ГОСТ 7076-99 таким же образом, как и для минеральной ваты.
В соответствии с ГОСТ 7076-99 теплопроводность определяют следующим образом:
Для проведения испытания применяют:
- прибор для измерения теплопроводности;
- электрошкаф сушильный, верхний предел нагрева которого не менее 383 К, предел допустимой погрешности задания и автоматического регулирования температуры - 5 К;
- штангенциркуль по ГОСТ 166-89 «Штангенциркули. Технические условия»: для измерения наружных и внутренних размеров с диапазоном измерения 0-125 мм, значением отсчета по нониусу - 0,05 мм, пределом допускаемой погрешности - 0,05 мм;
- линейка металлическая измерительная по ГОСТ 427-75 «Линейки измерительные металлические. Технические условия» с верхним пределом измерения 1000 мм, пределом допускаемого отклонения от номинальных значений длины шкалы и расстояний между любым штрихом и началом или концом шкалы – 0,2 мм;
- весы лабораторные электронные класс точности по ГОСТ 24104-2001 «Весы лабораторные. Общие технические требования» - II (высокий), с наибольшим пределом взвешивания 450 г, дискретность отсчета – 1 мг, пределы допускаемой погрешности в интервалах, мг:
от 0,02 до 50 г включ. ± 4 / 5
св. 50 до 200 г включ. ±7 / 10
св. 200 до 420 г включ. ±10 / 15.
Допускается применение других средств измерения с метрологическими характеристиками и оборудования с техническими характеристиками не хуже указанных в настоящем стандарте.
Подготовка образца к испытаниям заключается в следующем:
Толщину образца-параллелепипеда измеряют штангенциркулем в четырех углах и посередине каждой стороны. За толщину образца принимают среднеарифметическое значение результатов всех измерений.
Длину и ширину образца в плане измеряют линейкой.
Правильность геометрической формы и размеры образца теплоизоляционного материала определяют по ГОСТ 17177-94 «Материалы и изделия строительные теплоизоляционные. Методы испытаний».
Определяют массу образца М1 при его получении от изготовителя.
Образец высушивают до постоянной массы при температуре (60 ± 2) °С, указанной в нормативном документе на материал.
Образец считают высушенным до постоянной массы, если потеря его массы после очередного высушивания в течение 0,5 ч не превышает 0,1 %. По окончании сушки определяют массу образца М2 и его плотность ru, после чего образец немедленно помещают в прибор для определения теплопроводности.
Погрешность определения массы и размера образцов не должна быть более 0,5 %.
В результате была разработана двухступенчатая программа внутрилабораторного исследования:
I ступень – применяется стандартный подход, изложенный в СТБ ИСО 5725. На данной ступени выполняют следующие действия:
выявление источников изменчивости при измерении теплопроводности с позиций СТБ ИСО 5725;
определение характеристик валидации метода путем внутрилабораторного исследования;
планирование (выбор плана эксперимента) и проведение измерительного эксперимента;
проведение анализа полученных данных:
- проверка гипотезы о нормальном законе распределения результатов измерений;
- анализ результатов на наличие выбросов (критерии Кохрена и Граббса);
- определение характеристики прецизионности метода (в соответствии с СТБ ИСО 5725-3) – оценивание вкладов составляющих «m», «B» и «e»;
- определение характеристики смещения метода;
определение действительных значений характеристик метода.
II ступень – в случае, если анализ источников изменчивости не даст значительных результатов, включается вторая ступень, предполагающая более глубокое выявление процесса. Сюда можно отнести:
построение диаграммы «причина-следствие» с источниками изменчивости при измерении теплопроводности материалов с позиций руководства «Анализ измерительных систем» (MSA);
экспертиза всех источников изменчивости и выявление влияющих;
определение характеристики прецизионности метода (оценка влияния факторов с помощью дисперсионного анализа ANOVA).
Стоить отметить то, что в чистом виде каждую ступень, зачастую, реализовать не представляется возможным, поскольку они тесно переплетаются между собой. Поэтому, чтобы не нарушать последовательность проведения внутрилабораторного эксперимента, представим его в виде совокупности последовательных этапов таким образом, как они проводились в данной лаборатории:
выявление источников изменчивости при измерении теплопроводности с позиций СТБ ИСО 5725;
определение характеристик валидации метода путем внутрилабораторного исследования;
планирование и проведение измерительного эксперимента;
построение диаграммы «причина-следствие» с источниками изменчивости при измерении теплопроводности материалов;
экспертиза всех источников изменчивости и выявление влияющих;
проведение анализа полученных данных;
определение действительных значений характеристик метода.
Далее рассмотрим каждый из этих этапов.
1 этап. Выявление источников изменчивости при измерении теплопроводности с позиций СТБ ИСО 5725
В соответствии с СТБ ИСО 5725-3 каждый результат измерений y является суммой трех компонентов:
y = m + B + e,
где m – общее среднее значение (математическое ожидание);
B – лабораторная составляющая смещения согласно условиям повторяемости;
e – случайная ошибка, имеющая место при каждом измерении согласно условиям повторяемости (остаток).
Общее среднее значение «m» – это общее среднее арифметическое всех результатов измерений. Значение «m» зависит исключительно от «истинного значения» и метода измерений и не зависит от лаборатории, оборудования, оператора или времени, за которое был получен результат измерений.
В связи с тем, что теплопроводность представляет собой результат косвенных измерений, оценивание вклада метода um будет осуществляться с помощью модельного подхода.
Лабораторная составляющая «В» представляет собой отклонение лаборатории от «m» по той или иной причине безотносительно к случайной погрешности е, имеющей место в каждом результате измерений. Однако при постоянном использовании одного метода измерений становится очевидно, что в общем значении члена «В» воплощено большое число эффектов, которые вызваны, например, сменой оборудования, оператора, перекалибровкой, окружающей средой (температура, влажность, загрязнение воздуха и т.д.). поэтому статистическую модель можно переписать в форме:
y = m + B0 + B(1) + B(2) + … + e.
В рамках данной работы рассматривается влияние на результат измерений теплопроводности следующих источников изменчивости:
время: группы повторных результатов измерений были получены в разные дни;
оператор: измерения проводились двумя операторами.
Составляющая «е» представляет собой случайную погрешность, встречающуюся в каждом результате измерений.
Оценивание вкладов составляющих «В» и «е» осуществлялось на основании данных измерительного эксперимента.
Таким образом, к оцениванию точности результатов измерений теплопроводности был применен комбинированный метод: модельный подход – к оцениванию вклада составляющей «m» и подход на основе оценивания данных эксперимента – к оцениванию вклада составляющих «В» и «е».
2 этап. Определение характеристик валидации метода путем внутрилабораторного исследования
В данном эксперименте оцениванию подлежат следующие характеристики:
- промежуточная прецизионность;
- смещение.
Напомним, что это означает в соответствии с СТБ ИСО 5725-1:
Прецизионность – близость между независимыми результатами испытаний, полученными при определенных принятых условиях.
Промежуточная прецизионность – прецизионность в условиях, в которых результаты анализа получают по одной и той же методике, на идентичных пробах при вариации одного (например, время) или нескольких (например, исполнители и время) факторов из числа факторов, формирующих разброс результатов анализа при применении методики в конкретной лаборатории (МИ 2335).
Смещение – разность между математическим ожиданием результатов измерений и принятым эталонным значением.
3 этап. Планирование и проведение измерительного эксперимента
Отбор образцов (см. ранее)
Определение условий измерений
В данной лаборатории измерительный эксперимент осуществлялся в условиях промежуточной прецизионности. Это было обусловлено тем, что измерения теплопроводности стационарными методами – процесс достаточно длительный. Измерения одного образца занимают несколько часов, а на проведение эксперимента в целом ушло несколько дней. В то же время измерения проводились различными операторами.
Выбор плана эксперимента
Существует 2 вида планов:
- факторные;
- иерархические.
Факторные планы (например, полнофакторные) позволяют найти как регрессионную модель у, так и дисперсионный анализ. Недостаток данного вида планов – они большие.
Иерархические позволяют провести только дисперсионный анализ. Достоинство – они короче факторных планов.
В свою очередь, в СТБ ИСО 5725-3 описаны два вида плана иерархического эксперимента:
план эксперимента с полной группировкой;
план эксперимента со ступенчатой группировкой (например, три результата измерений получены в условиях повторяемости, а четвертый результат – в условиях промежуточной прецизионности, этот план требует получения меньшего количества результатов измерений, но в то же время анализ является более сложным и имеется большая неопределенность в оценках стандартных отклонений из-за меньшего количества результатов измерений).
В данной работе рассматривается измерительный эксперимент, осуществленный по плану с полной группировкой. Эксперимент проводился в одной лаборатории с двумя различными видами материалов (минеральная вата и пенополистирол). Были использованы образцы из различных материалов (минеральная вата и пенополистирол), различной толщины (30 и 50 мм) и при различных средних значениях температуры поверхностей образца (10 С и 25 С).
На рисунке А.5 приведен схематический план проведенного эксперимента.

Рисунок А.5 – План измерительного эксперимента по определению теплопроводности
На верхнем уровне – материал, используемый в измерительном эксперименте, фактор i – толщина образца, фактор j – средняя температура поверхностей образца в эксперименте, фактор k – номер повторения согласно условиям повторяемости. В итоге для одного материала было проведено 4 опыта по 5 измерений в каждом.
Проведение измерительного эксперимента
В таблице А.3 представлены результаты измерений.
Таблица А.3 – Результаты измерений теплопроводности образцов
Материал |
№ опыта |
№ изм. |
Тср, С |
h, м |
Т, C |
QB, мкВ |
QH, мкВ |
λ, Вт/(м·К) |
|
Минеральная вата
|
1 |
1 2 3 4 5 |
9,95 9,67 9,84 9,85 9,33 |
0,32328 0,30917 0,30778 0,28817 0,31285 |
10,00 9,99 9,86 9,98 9,96 |
2328 2427 2133 2600 2266 |
1962 2132 2237 2240 2114 |
0,03613 0,03705 0,03574 0,03663 0,03591 |
|
|
|
2 |
1 2 3 4 5 |
25,21 25,90 25,28 25,48 25,41 |
0,32391 0,31035 0,30858 0,28911 0,31349 |
9,95 9,97 9,97 9,95 10,01 |
2353 2342 2541 2662 2472 |
2038 2360 2000 2344 2081 |
0,03897 0,03850 0,04006 0,03966 0,03895 |
|
3 |
1 2 3 4 5 |
9,5 9,17 9,43 9,59 9,6 |
0,47901 0,48445 0,47771 0,47261 0,47169 |
10,04 10,16 10,01 10,00 10,04 |
1601 1333 1637 1393 1342 |
1330 1555 1235 1564 1641 |
0,03653 0,03604 0,03590 0,03649 0,03686 |
|
|
4 |
1 2 3 4 5 |
25,46 25,24 25,89 25,01 25,33 |
0,47598 0,48462 0,4785 0,47325 0,47175 |
10,02 9,99 9,96 9,96 9,95 |
1921 1756 1528 1667 1620 |
1124 1165 1441 1337 1393 |
0,03978 0,03859 0,03900 0,03899 0,03892 |
|
|
Пенополистирол |
5 |
1 2 3 4 5 |
10,03 10,03 10,17 9,90 10,07 |
0,30973 0,309 0,31039 0,30685 0,30901 |
10,03 10,05 9,99 10,01 10,06 |
1915 1942 1935 1928 1900 |
1743 1759 1713 1772 1790 |
0,02950 0,02981 0,02968 0,02975 0,02973 |
|
6 |
1 2 3 4 5 |
25,23 25,33 25,36 25,42 25,13 |
0,31059 0,31132 0,3113 0,30803 0,3103 |
9,96 10,06 10,05 9,97 9,98 |
2024 1975 1959 2016 1972 |
1736 1829 1846 1797 1817 |
0,03205 0,03212 0,03215 0,03216 0,03206 |
|
|
7 |
1 2 3 4 5 |
9,96 9,30 10,08 10,12 9,40 |
0,48647 0,48648 0,4889 0,48644 0,48648 |
9,97 9,95 10,02 10,00 10,05 |
1834 1806 1868 1901 1200 |
1678 1705 1651 1680 1133 |
0,02957 0,02957 0,02957 0,02931 0,02954 |
|
|
8 |
1 2 3 4 5 |
25,26 25,29 25,46 25,33 25,14 |
0,48724 0,48718 0,4900 0,4872 0,48724 |
10,00 9,95 9,95 9,92 10,08 |
1968 1873 1899 1918 1231 |
1653 1739 1719 1770 1172 |
0,03177 0,03201 0,03193 0,03191 0,03172 |
|
|
Примечание – Значение коэффициента калибровки составляет: - при 10 С – N = 0,00522; - при 25 С – N = 0,00546 |
||||||||
4 этап. Построение диаграммы «причина-следствие» с источниками изменчивости при измерении теплопроводности материалов с позиций руководства «Анализ измерительных систем» (MSA)
Диаграмма «причина-следствие» с источниками изменчивости при измерении теплопроводности материалов представлена на рисунке А.6.

Рисунок А.6 – Диаграмма «причина-следствие» с источниками изменчивости при измерении теплопроводности материалов с помощью прибора HFM 436
Окружающая среда характеризуется условиями, в которых выполняются измерения. Условия выполнения измерений нормируются и должны соответствовать установленным значениям. Условия выполнения измерений включают в себя:
атмосферное давление;
влажность воздуха;
температура.
Влияние оператора на результаты измерений можно объяснить его квалификацией (образование), компетентностью (наличие знаний и опыта работы) и психофизиологическим состоянием (состояние здоровья, утомленность, настроение и т.д.).
Влияние образца на результаты измерений можно объяснить следующими характеристиками:
а) стабильность свойств:
1) стабильность теплотехнических свойств;
Теплопроводность материала по своей природе имеет свойство изменяться под действием определенных факторов. В связи с этим измерения теплопроводности при проведении исследований необходимо осуществлять по возможности в наиболее короткие сроки и при фиксированных значениях воздействий;
2) влияние упругих свойств материала объясняется тем, что при сжатии образца из мягкого материала (например, минеральной ваты) уменьшается объемная доля воздуха в его порах. Это приводит к увеличению теплопроводности, а следовательно и к ухудшению теплотехнических характеристик материала;
б) геометрия (макрогеометрия);
Для предотвращения появления контактного сопротивления между рабочими поверхностями измеряемых образцов и плитами прибора необходимо обеспечить плотный контакт между ними. Поэтому рабочие поверхности образцов следует соответствующим образом обрабатывать перед выполнением измерений (часто применяют шлифование);
в) гомогенность материала;
Гомогенный пористый материал – материал, в котором локальная пористость не зависит от точки, в которой рассчитывается значение теплопроводности. Пористость – общий объем пустот в пористом материале, деленный на общий объем материала. Механическая гомогенность характеризуется равномерным распределением механических примесей по всему объему материала. Негомогенность материала (как воздушная, так и механическая) приводит к искажению результатов измерения теплопроводности, занижая или завышая их значения.
Влияние измерительного прибора на результаты измерений определяется следующими составляющими:
а) влияние измерения толщины связано с:
1) измерительной системой линейных перемещений, включающей в себя:
- неопределенность измерительной системы линейных перемещений;
- многократные измерения толщины образца – описываются стандартным отклонением результатов измерений толщины образца;
2) отклонением от параллельности плит прибора;
3) отклонением от плоскостности плит прибора;
б) влияние измерения разности температур:
1) измерение температуры плит обусловлено:
- неопределенностью программируемого логического контроллера;
- нестабильностью термопары – изменение показаний при одном и том же значении температуры с течением времени;
2) прочие источники:
- контактное сопротивление;
- измерение средней температуры плоской плиты;
в) влияние измерения тепловых потоков характеризуется измерением входной мощности, которое обусловлено следующими составляющими:
1) калибровка эталонного резистора – установление действительного значения сопротивления с отклонением;
2) дрейф эталонного резистора – изменение сопротивления во времени;
3) измерение напряжения на резисторе;
4) входная мощность датчика теплового потока.
5 этап. Экспертиза всех источников изменчивости и выявление влияющих
По результатам экспертного оценивания источников изменчивости наиболее сильно влияющими были признаны источники, вызываемые:
нестабильностью теплотехнических и свойств исследуемого материала;
нестабильностью упругих свойств исследуемого материала;
отклонением от параллельности рабочих поверхностей образца;
негомогенностью исследуемого материала (приводит к искажению результатов измерения теплопроводности, занижая или завышая их значения);
неточностью определения разности температур плит прибора;
неточностью измерения толщины образца.
6 этап. Проведение анализа полученных данных
Проверка гипотезы о нормальном законе распределения результатов измерений
Полученную совокупность результатов измерений перед проведением внутрилабораторного исследования необходимо проверить на соответствие гипотезе о нормальном законе распределения.
Считается, что чем больше количество результатов, тем больше степень доверия к результату применения критерия. Исходя из этого, для проверки гипотезы о нормальном законе распределения часто используют критерий Пирсона χ2 – «хи-квадрат».
Для осуществления проверки необходимо выполнить 50 измерений.
В связи с тем, что в нашем случае, число результатов измерений в каждом опыте составляет 5, выполнить проверку на соответствие совокупности результатов измерений гипотезе о нормальном законе распределения по критерию Пирсона не представляется возможным. Поэтому для упрощения расчетов будет принято, что результаты измерений распределены по нормальному закону.
Анализ результатов на наличие выбросов
2.1) Числовой метод выбросов
Для рассмотрения выбросов рекомендуется следующая методика.
а) Для идентификации разбросов или выбросов критерии применяются Кохрена и Граббса.
б) Далее проводится исследование с целью выяснения, могут ли разбросы и/или статистические выбросы быть объяснены какой-либо технической ошибкой, например:
- промах при выполнении измерений;
- ошибка в расчётах;
- элементарная описка при переписывании результата измерений.
В том случае, где ошибка являлась следствием расчётов или переписывания, сомнительный результат должен быть заменён правильным значением. В том случае, когда такого рода замена невозможна, данный результат исключается из совокупности. После произведения корректировок, проверка на предмет разбросов или выбросов повторяется;
в) В случае, когда какие-либо разбросы и/или статистические выбросы остаются необъяснёнными или исключенными в качестве принадлежащих к выбросам, то разбросы сохраняются в качестве корректных позиций, а статистические выбросы исключаются.
Критерий Кохрена представляет собой критерий внутрилабораторной изменчивости и должен применяться в первую очередь, причем, при его отвержении должны быть приняты какие-либо действия с повторными измерениями. Другой критерий (Граббса), главным образом, представляет собой критерий межгрупповой изменчивости и также может использоваться в тех случаях, где проверка с применением критерия Кохрена вызвала подозрение относительно того, можно ли отнести высокую внутрилабораторную дисперсию только к одному из результатов измерений в группе.
Группы результатов подлежат обработке, в ходе которой рассчитывают средние арифметические значения и стандартные отклонения для каждой группы.
Среднее значение для группы результатов рассчитывается по формуле:

где λij – i-ый результат измерения в j-ой группе результатов измерений.
n – количество повторных результатов измерений.
Стандартное отклонение для группы результатов рассчитывается по следующей формуле:

Результаты расчетов представлены в таблице А.4.
Таблица А.4 – Расчет средних значений и стандартных отклонений
Материал |
№ опыта |
№ изм. |
λ, Вт/(м·К) |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
Минеральная вата |
1 |
1 2 3 4 5 |
0,03613 0,03705 0,03574 0,03663 0,03591 |
0,036292 |
0,000539 |
2 |
1 2 3 4 5 |
0,03897 0,04006 0,03850 0,03966 0,03895 |
0,039228 |
0,000623 |
|
3 |
1 2 3 4 5 |
0,03653 0,03604 0,0359 0,03649 0,03686 |
0,036364 |
0,000390 |
|
4 |
1 2 3 4 5 |
0,03978 0,03859 0,03900 0,03899 0,03892 |
0,039056 |
0,000438 |
|
Пенополистирол |
1 |
1 2 3 4 5 |
0,02950 0,02981 0,02968 0,02975 0,02973 |
0,029694 |
0,000118 |
2 |
1 2 3 4 5 |
0,03205 0,03212 0,03215 0,03216 0,03206 |
0,032108 |
0,000051 |
|
3 |
1 2 3 4 5 |
0,02957 0,02957 0,02957 0,02931 0,02954 |
0,029512 |
0,000114 |
|
4 |
1 2 3 4 5 |
0,03177 0,03201 0,03193 0,03191 0,03172 |
0,031868 |
0,000120 |
2.2) Анализ результатов измерений на наличие выбросов по критерию Кохрена
При наличии совокупности из p стандартных отклонений sj, которые рассчитаны исходя из одного и того же количества (n) повторных результатов, статистика С, лежащая в основе критерия Кохрена, представляет собой:
|
|
где smax - наибольшее стандартное отклонение в совокупности.
Полученные значения статистик сравниваются с критическими значениями:
- в том случае, если статистика, меньше или равна своего 5 % -ого критического значения, то исследуемая позиция признаётся корректной;
- в том случае, если статистика, больше своего 5 % -ого критического значения и меньше или равна своему 1 % -ому критическому значению, то исследуемой позиции присваивается название разброса, и она отмечается одной звёздочкой;
- в том случае, если статистический критерий больше своего 1 % -ого критического значения, то позиции присваивается название статистического выброса, и она отмечается двумя звёздочками.
В таблице А.5 представлены результаты расчета статистики Кохрена. По стандартной таблице для p = 4 и n = 5 находим значения 5 % -ого и 1 % -ого критического значения.
Таблица А.5 – Расчет статистики Кохрена
Материал |
|
, Вт/(м·К) |
|
|
С |
С1% |
C5% |
Минеральная вата |
1 |
0,000539 |
2,9·10-7 |
3,9·10-7 |
0,382 |
0,721 |
0,629 |
2 |
0,000623 |
3,9·10-7 |
|||||
3 |
0,000390 |
1,5·10-7 |
|||||
4 |
0,000438 |
1,9·10-7 |
|||||
Сумма |
10,2·10-7 |
|
|||||
Пенополистирол |
5 |
0,000118 |
1,4·10-8 |
1,3·10-8 |
0,271 |
0,721 |
0,629 |
6 |
0,000051 |
2,6·10-9 |
|||||
7 |
0,000114 |
1,3·10-8 |
|||||
8 |
0,000120 |
1,4·10-8 |
|||||
Сумма |
4,4·10-8 |
|
|||||
Таким образом, расчеты показали, что выбросы и разбросы среди всей совокупности наблюдений отсутствуют.
2.3) Анализ результатов измерений на наличие выбросов по критерию Граббса
Расчет критерия Граббса производится для двух случаев:
наличие в совокупности результатов одного выбросового наблюдения;
наличие в совокупности результатов двух выбросовых наблюдений.
Так как выбросовые значения у нас отсутствуют, нет необходимости проводить анализ по критерию Граббса.
3) Определение характеристики прецизионности метода
В соответствии с СТБ ИСО 5725-3 каждый результат измерений y является суммой трех компонентов (см. 1 этап).
В свою очередь дисперсия результата измерений также является суммой дисперсий трех компонентов:
Dy = Dm + DB + De.
Необходимо произвести оценку каждой из дисперсий.
3.1) Оценивание вклада метода при измерении теплопроводности – составляющей «m»
В связи с тем, что теплопроводность – результат косвенного измерения, можно оценить стандартную неопределенность um используя модельный подход.
Теплопроводность является результатом косвенных измерений (см. формулу теплопроводности).
После применения к формуле теплопроводности метода относительных неопределенностей (отношение абсолютной неопределенности к результату измерений) получается:
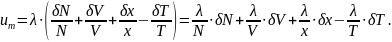
В свою очередь

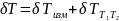
В результате

Первым слагаемым (коэффициент калибровки датчика теплового потока при температуре t) можно пренебречь в связи с тем, что данная величина второго порядка малости (при 10 С – N = 0,00522; при 25 С – N = 0,00546).
Входные величины с указанием применяемых обозначений и единиц измерений, в которых они будут оцениваться, представлены в таблице А.6.
Таблица А.6 – Входные величины
Величина |
Единица измерений |
Определение или описание |
|
мкВ |
Поправка, обусловленная точностью определения теплового потока |
|
м |
Поправка, обусловленная точностью определения толщины образца |
|
м |
Поправка, обусловленная влиянием фактора «толщина образца» |
|
К (С) |
Поправка, обусловленная точностью определения разности температур горячей и холодной плит прибора |
|
К (С) |
Поправка, обусловленная влиянием фактора «средняя температура поверхностей образца» |
Анализ входных данных представлен в таблице А.7.
Таблица А.7 – Анализ входных данных
Входная величина |
Описание |
|
Тип неопределенности: В Вид распределения: прямоугольное Значение оценки: 0 мкВ Стандартная
неопределенность:
где ± y1 определяется как пределы абсолютной погрешности датчика теплового потока |
|
Тип неопределенности: В Вид распределения: прямоугольное Значение оценки: 0 м Стандартная
неопределенность:
u(
)
где ± y2 определяется как пределы абсолютной погрешности средства измерений толщины |
|
Тип неопределенности: А Вид распределения: нормальное Значение оценки: 0 м Стандартная
неопределенность:
Расчет
|
|
Тип неопределенности: В Вид распределения: прямоугольное Значение оценки: 0 м Стандартная
неопределенность: u(
)
где ± y3 определяется как пределы абсолютной погрешности датчиков температуры |
|
Тип неопределенности: А Вид распределения: нормальное Значение оценки: 0 м Стандартная
неопределенность:
Расчет
|
Далее составляется бюджет неопределенности для оценивания отклонений теплопроводности прибора HFM 436 (таблица А.8).
Таблица А.8 – Форма представления бюджета неопределенности
Входная величина |
Единица измерения |
Значение оценки |
Тип неопределенности |
Распределение вероятностей |
Стандартная неопределенность |
Коэффициент чувствительности |
Вклад в неопределенность, Вт/(м·К) |
|
мкВ |
0 |
B |
прямоугольное |
|
|
|
|
м |
0 |
В |
прямоугольное |
|
|
|
|
м |
0 |
А |
нормальное |
|
|
|
|
С |
0 |
В |
прямоугольное |
|
|
|
|
С |
0 |
А |
нормальное |
|
|
|
|
Вт/(м·K) |
|
- |
- |
|
- |
- |
Оценка влияния факторов «толщина образца» и «средняя температура поверхностей образца» выполняется с помощью дисперсионного анализа (ANOVA). В дисперсионном анализе проверяется гипотеза о равенстве математических ожиданий выходного контролируемого параметра (λ) при влиянии на него различных факторов (х, t). Выдвигается нулевая гипотеза Н0, которая состоит в том, что влияния факторов х и t на результат измерения отсутствуют. Гипотеза принимается, то есть влияния факторов отсутствуют, если уровень значимости р > 0,05. И гипотеза отвергается, то есть факторы влияют на результат измерения, когда уровень значимости р < 0,05.
Пусть на количественный нормально распределенный признак λ воздействует два фактора х и t, которые имеют соответственно r = 2 и q = 2 постоянных уровней. Число измерений в каждом pq сочетании одинаково и равно n = 5. Всего проведено N = n·r·q = 20 измерений. Результаты измерений представим в виде λijk (k = 1, 2 (х); j = 1, 2 (t); i = 1, 2,…, 5 (n)).
В таблице А.9 представлены исходные данные для выполнения дисперсионного анализа результатов измерений теплопроводности минеральной ваты.
Таблица А.9 – Исходные данные для дисперсионного анализа
Материал |
t х |
х1 = 30 мм |
х2 = 50 мм |
Минеральная вата |
t1 = 10 С |
0,03613 |
0,03653 |
0,03705 |
0,03604 |
||
0,03574 |
0,03590 |
||
0,03663 |
0,03649 |
||
0,03591 |
0,03686 |
||
t2 = 25 С |
0,03897 |
0,03978 |
|
0,04006 |
0,03859 |
||
0,03850 |
0,03900 |
||
0,03966 |
0,03899 |
||
0,03895 |
0,03892 |
Необходимо вычислить групповые средние и общее среднее значений результатов измерений по формулам:

Средние значения результатов в каждой из четырех групп результатов измерений в соответствии с данными таблицы А.9:
 Вт/(м·К);
Вт/(м·К);
 Вт/(м·К);
Вт/(м·К);
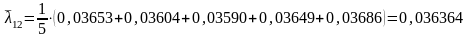 Вт/(м·К);
Вт/(м·К);
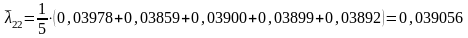 Вт/(м·К).
Вт/(м·К).
Среднее значение результатов измерений, выполненных при различной средней температуре поверхностей образца, вычисляется по формуле:
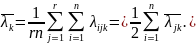
Таким образом, подставим данные в формулу, получим следующее среднее значение результатов измерений, выполненных при номинальной средней температуре поверхностей образца 10 С:
 Вт/(м·К).
Вт/(м·К).
Среднее значение результатов измерений, выполненных при номинальной средней температуре поверхностей образца 25 С:
 Вт/(м·К).
Вт/(м·К).
Среднее значение результатов измерений, выполненных для образцов различной толщины, вычисляется по формуле:

Таким образом, среднее значение результатов измерений, выполненных для образцов номинальной толщины 30 мм:
 Вт/(м·К).
Вт/(м·К).
Среднее значение результатов измерений, выполненных для образцов номинальной толщины 50 мм:
 Вт/(м·К).
Вт/(м·К).
Тогда общее среднее будет вычисляться по формуле:

Подставив данные в формулу, получим:
 Вт/(м·К).
Вт/(м·К).
Для более наглядного представления дисперсионного анализа, приведем проведенные ранее манипуляции в виде диаграммы, представленной на рисунке А.7.

Рисунок А.7 – Схема проведения дисперсионного анализа
В результате дисперсионного анализа необходимо произвести расчет, представленный в таблице А.10.
Таблица А.10 – Таблица дисперсионного анализа для двухфакторного эксперимента
Источник изменчивости |
Суммы квадратов |
Степени свободы |
Средние квадраты |
Влияние фактора А |
|
r-1 |
|
Влияние фактора В |
|
q-1 |
|
Взаимодействие факторов А и В |
|
(r-1)·(q-1) |
|
Случайная ошибка |
|
N-r·q |
|
Результаты расчета представлены в таблице А.11.
Таблица А.11 – Таблица результатов дисперсионного анализа для двухфакторного эксперимента
Источник изменчивости |
Суммы квадратов |
Степени свободы |
Средние квадраты |
Влияние фактора h |
Sh2 = 1,25 10-5 |
1 |
Mh =1,25 10-5 |
Влияние фактора T |
ST2= 1,25 10-5 |
1 |
|
Взаимодействие факторов h и T |
ShT2 =7,4 10-8 |
1 |
|
Случайная ошибка |
|
16 |
|
Выдвигается гипотеза Н0, которая состоит в том, что рассматриваемые факторы не оказывают влияния на результат измерений.
Для проверки гипотезы производят сравнение отношения среднего квадрата для рассматриваемого фактора и среднего квадрата для случайной ошибки с F-распределением с соответствующими степенями свободы при уровне значимости α.
Если вычисленное значение больше табличного, то выдвинутая гипотеза ложна при принятом уровне значимости α. Уровень значимости принимается чаще всего α = 5 %.
Таким образом, получаем:
для случая взаимодействия факторов x и t
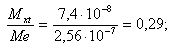
для случая влияния фактора х

для случая влияния фактора t
![]()
Табличное
значение F-распределения
для числа степеней свободы
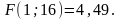
Таким образом, можно сделать вывод, что на результаты измерений теплопроводности образца из минеральной ваты оказывает влияние средняя температура поверхностей образца (156,3 > 4,49). Остальные факторы не оказывают существенного влияния на результаты измерений теплопроводности.
Проведем дисперсионный анализ для второго материала – пенополистирола.
Он проводится аналогично дисперсионному анализу для минеральной ваты. Представим окончательные результаты.
Результаты измерений представлены в таблице А.12.
Таблица А.12 – Таблица исходных данных для дисперсионного анализа
Материал |
t х |
х1=30 мм |
х2=50 мм |
Пенополистирол |
t1=10 С |
0,02950 |
0,02957 |
0,02981 |
0,02957 |
||
0,02968 |
0,02957 |
||
0,02975 |
0,02932 |
||
0,02973 |
0,02954 |
||
t2=25 С |
0,03205 |
0,03177 |
|
0,03212 |
0,03201 |
||
0,03215 |
0,03193 |
||
0,03216 |
0,03191 |
||
0,03206 |
0,03172 |
Результаты расчета дисперсионного анализа представлены таблице А.13.
Таблица А.13 – Таблица результатов дисперсионного анализа для двухфакторного эксперимента
Источник изменчивости |
Суммы квадратов |
Степени свободы |
Средние квадраты |
Влияние фактора х |
|
1 |
|
Влияние фактора t |
|
1 |
|
Взаимодействие факторов х и t |
|
1 |
|
Случайная ошибка |
|
16 |
|
Осуществим проверку гипотезы Н0 о влиянии факторов на результаты измерений. Таким образом, получаем:
для случая взаимодействия факторов x и t

для случая влияния фактора х
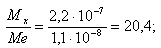
для случая влияния фактора t
![]()
Табличное значение F-распределения для числа степеней свободы
Таким образом, можно сделать вывод, что на результаты измерений теплопроводности образца из пенополистирола оказывает влияние как толщина образца (20,4 > 4,49), так и средняя температура поверхностей образца (2600,9 > 4,49).
Суммарные стандартные неопределенности отклонений значений теплопроводности от действительных значений вычисляются по формуле:

С учетом полученных результатов для факторов «толщина образца» и «средняя температура поверхностей образца» необходимо провести оценивание вкладов в неопределенность измерений теплопроводности. Данный расчет был проведен для каждого из опытов отдельно.
Опыт №1: материал – минеральная вата, толщина образца х = 30 мм, средняя температура поверхностей образца Тср = 10 С. Результаты измерений представлены в таблице А.14.
Таблица А.14 – Результаты измерений теплопроводности в опыте №1
№ изм. |
Тср, С |
x, м |
T, C |
QB, мкВ |
QH, мкВ |
λ, Вт/(м·К) |
1 |
9,95 |
0,32328 |
9,95 |
2328 |
1962 |
0,03613 |
2 |
9,67 |
0,30917 |
9,67 |
2427 |
2132 |
0,03705 |
3 |
9,84 |
0,30778 |
9,84 |
2133 |
2237 |
0,03574 |
4 |
9,85 |
0,28817 |
9,85 |
2600 |
2240 |
0,03663 |
5 |
9,33 |
0,31285 |
9,33 |
2266 |
2114 |
0,03591 |
Составим бюджет неопределенности (таблица А.15).
Таблица А.15 – Бюджет неопределенности
Входная величина |
Единица измерения |
Значение оценки |
Интервал |
Тип неопределенности |
Распределение вероятностей |
Стандартная неопределенность |
Коэффициент чувствительности |
Вклад в неопределенность, Вт/(м·К) |
𝛿V |
мкВ |
0 |
± 3 |
B |
прямоугольное |
1,7 |
1,6·10-5 |
2,7·10-5 |
|
м |
0 |
± 0,0005 |
В |
прямоугольное |
0,0003 |
0,12 |
3,6·10-5 |
|
м |
0 |
- |
А |
нормальное |
0,0001 |
0,12 |
1,2·10-5 |
|
С |
0 |
± 0,5 |
В |
прямоугольное |
0,3 |
3,6·10-3 |
1,1·10-3 |
|
С |
0 |
- |
А |
нормальное |
0,0063 |
3,6·10-3 |
2,3·10-5 |
|
Вт/(м·K) |
|
|
- |
- |
1,1·10-3 |
- |
- |
По результатам расчета можно сделать вывод, что наибольший вклад в неопределенность вносит составляющая δТизм.
Для большей наглядности результаты расчетов можно представить в виде диаграммы (рисунок А.8).
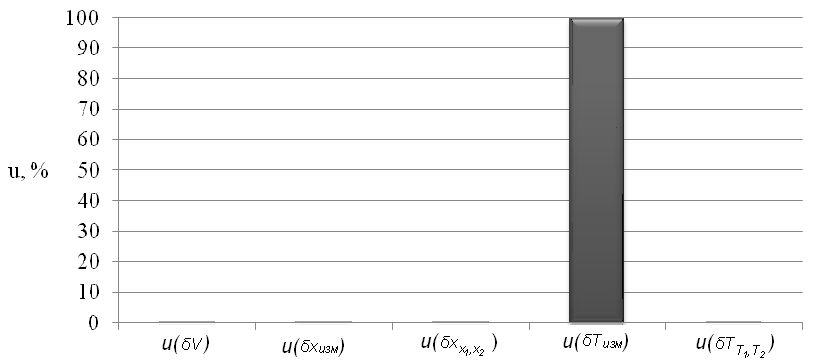
Рисунок А.8 – Диаграмма влияния всех составляющих на суммарную стандартную неопределенность
Изобразим отдельно на диаграмме влияние составляющих δV, δxизм, δxх1,х2, δТТ1,Т2 (рисунок А.9).
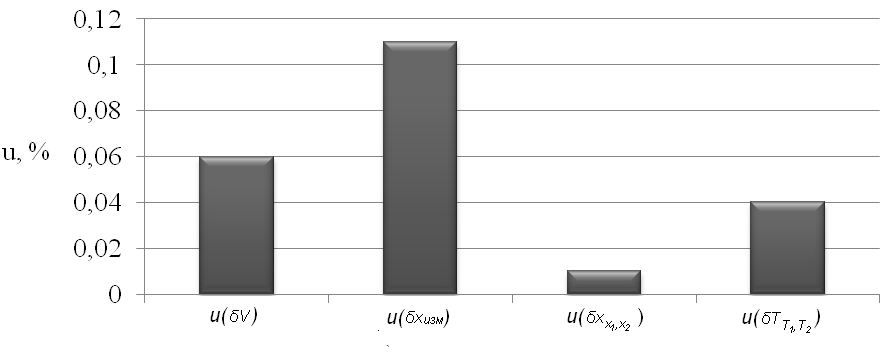
Рисунок А.9 – Диаграмма влияния составляющих δV, δxизм, δxх1,х2, δТТ1,Т2 на суммарную стандартную неопределенность
В данном случае наибольшее влияние оказывает составляющая δxизм, но в то же время она пренебрежимо мала по сравнению с составляющей δТизм.
Рассчитаем суммарную стандартную неопределенность для опыта №1. В результате получим:
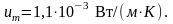
Аналогично рассчитываем стандартные неопределенности и выявляем какая из составляющих вносит наибольший вклад в неопределенность для всех остальных опытов. Результаты представлены в таблице А.16.
Таблица А.16 – Стандартные неопределенности по всем опытам
Материал |
№ опыта |
um, Вт/(м·К) |
Минеральная вата |
1 2 3 4 |
0,0011 0,0012 0,0011 0,0012 |
Пенополистирол |
1 2 3 4 |
0,00087 0,00096 0,00087 0,00096 |
По результатам всех проведенных расчетов было выявлено, что наибольший вклад в суммарную стандартную неопределенность вносит составляющая δТизм.
3.2) Оценивание вклада лабораторной составляющей при измерении теплопроводности – составляющей «В»
Множество различных факторов (помимо вариаций между предположительно идентичными образцами) может способствовать изменчивости результатов в зависимости от метода измерений, в том числе:
оператор;
используемое оборудование;
калибровка оборудования;
условия окружающей среды (температура, влажность, загрязнение воздуха и т.д.);
время, проходящее между измерениями.
По всей видимости факторами, наиболее сильно влияющими на прецизионность метода измерений, являются следующие четыре:
время: насколько большим был интервал между последовательными измерениями;
калибровка: производилась ли калибровка одного и того же оборудования между последовательными группами измерений;
оператор: один или несколько операторов выполняют последовательные измерения;
оборудование: одно и то же или различное оборудование использовались при измерениях.
С целью установления степени влияния отдельных факторов на результаты измерений проводятся факторные эксперименты. Факторный эксперимент – эксперимент, в котором все уровни каждого фактора сочетаются со всеми уровнями остальных факторов.
Необходимо чтобы факторы, влияющие на измерения и определяющие эти определенные условия, изменялись от группы к группе в строго определенном порядке и чтобы все исследуемые уровни каждого фактора, сочетались со всеми уровнями остальных факторов.
Для исследования влияния всех уровней факторов на результаты измерений используется дисперсионный анализ. В зависимости от количества изменяемых в эксперименте факторов различают однофакторные, двухфакторные, трехфакторные и n-факторные эксперименты.
Для получения результатов, наиболее полно описывающих метод измерения, необходимо было бы провести четырехфакторный эксперимент. Однако это не представляется возможным в связи с тем, что количество экземпляров оборудования в лаборатории ограничено.
В данной работе рассматривается внутрилабораторный двухфакторный эксперимент. На результат измерения воздействует два фактора:
А: оператор;
В: время.
Как правило, составляющая В оценивается одновременно с исследованием е (ue). Реализуется это, например, иерархическим планом по СТБ ИСО 5725-3 так, как представлено на рисунке А.10.
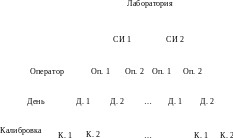
Рисунок А.10 – Иерархический план измерительного эксперимента
Исходя из рисунка А.10 получается: 16 экспериментов × 5.
Источники изменчивости в таблице дисперсионного анализа по результатам плана будут следующие:
Источник изменчивости |
М |
Общая → σR внутрилабораторная воспроизводимость |
|
Вклад СИ |
|
Вклад персонала |
|
Вклад день |
|
Вклад калибровка |
|
Вклад СИ, персонала |
|
… |
|
Вклад е → σr |
Ме |
Для целей верификации (исследования) нас интересует вся таблица дисперсионного анализа, из которой мы оцениваем составляющие вкладов от каждого фактора Вi, i =1…4, их попарного, тройного и четвертного (корреляция) взаимодействия.
Цель верификации на данном этапе – минимизировать значительные вклады путем организационных, технических и других мероприятий.
В рамках данного исследования оценивание вклада лабораторной составляющей не представляется возможным в связи с отсутствием информации о том, какие результаты измерений кем из операторов и в какой день были получены. По этой причине прибегнув к экспертному оцениванию, на основании предыдущего опыта аккредитованной лаборатории, было решено принять ее равной 5 %.
3.3) Оценивание вклада повторяемости при измерении теплопроводности – составляющей «е»
В каждом из опытов получено по пять результатов измерений. В данном случае для оценивания повторяемости рассчитывают стандартное отклонение среднего арифметического значения в каждой группе полученных результатов.
Сначала рассчитывают среднее значение в каждой группе полученных результатов по формуле

где λij – i-й результат измерений в j-м опыте;
n – количество повторных измерений в опыте.
Затем необходимо рассчитать стандартное отклонение результатов измерений в каждом опыте по формуле

Тогда оценивание повторяемости при измерениях будет осуществляться по формуле

В таблице А.17 представлены результаты расчета оценки повторяемости для каждого из опытов.
Таблица А.17 – Результаты расчета оценки повторяемости
Материал |
№ опыта |
№ изм. |
λ, Вт/(м·К) |
, Вт/(м·К) |
, Вт/(м·К) |
|
|
Минеральная вата |
1 |
1 2 3 4 5 |
0,03613 0,03705 0,03574 0,03663 0,03591 |
0,036292 |
0,000539 |
0,00024 |
|
2 |
1 2 3 4 5 |
0,03897 0,04006 0,03850 0,03966 0,03895 |
0,039228 |
0,000623 |
0,00028 |
||
3 |
1 2 3 4 5 |
0,03653 0,03604 0,0359 0,03649 0,03686 |
0,036364 |
0,000390 |
0,00017 |
||
|
|
4 |
1 2 3 4 5 |
0,03978 0,03859 0,03900 0,03899 0,03892 |
0,039056 |
0,000438 |
0,00019 |
|
Пенополистирол |
1 |
1 2 3 4 5 |
0,02950 0,02981 0,02968 0,02975 0,02973 |
0,029694 |
0,000118 |
0,000053 |
|
2 |
1 2 3 4 5 |
0,03205 0,03212 0,03215 0,03216 0,03206 |
0,032108 |
0,000120 |
0,000054 |
|
|
3 |
1 2 3 4 5 |
0,02957 0,02957 0,02957 0,02931 0,02954 |
0,029512 |
0,000114 |
0,000051 |
|
|
4 |
1 2 3 4 5 |
0,03177 0,03201 0,03193 0,03191 0,03172 |
0,031868 |
0,000120 |
0,000054 |
|
3.4) Определение характеристики смещения метода
В рамках данной работы определение характеристики смещения не представляется возможным в связи с отсутствием стандартных образцов из пенополистирола и минеральной ваты с принятым эталонным значением теплопроводности.
В условиях наличия стандартных образцов определение характеристики смещения необходимо осуществлять по следующей методике:
оценка
 лабораторного смещения
лабораторного смещения
 находится по формуле
находится по формуле

где
 - среднее значение результатов измерений;
- среднее значение результатов измерений;
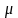 -
принятое эталонное значение теплопроводности
стандартного образца.
-
принятое эталонное значение теплопроводности
стандартного образца.
7 этап. Определение действительных значений характеристик метода
В связи с отсутствием стандартных образцов, определение характеристики смещения не представляется возможным.
Характеристики прецизионности метода в соответствии с СТБ ИСО 5725 по результатам исследования представлены в таблице А.18.
Таблица А.18 – Хактеристики прецизионности метода по результатам исследования
Материал |
№ опыта |
um, Вт/(м·К) |
uB, Вт/(м·К) |
ue, Вт/(м·К) |
u, Вт/(м·К) |
1 |
2 |
3 |
4 |
5 |
6 |
Минеральная вата |
1 2 3 4 |
0,0011 0,0012 0,0011 0,0012 |
0,00026 0,00028· 0,00026 0,00029 |
0,00024 0,00028 0,00017 0,00019 |
0,0012 0,0013 0,0011 0,0012 |
Пенополистирол |
1 2 3 4 |
0,00087 0,00096 0,00087 0,00096 |
0,00020 0,00022 0,00019 0,00022 |
0,000053 0,000023 0,000051 0,000054 |
0,00089 0,00099 0,00089 0,00099 |
Для удобства представления на диаграмме определим вклады в в суммарную неопределенность каждой из составляющих um, uB, ue в процентах (таблица А.19).
Таблица А.19 – Вклады в суммарную неопределенность отдельных составляющих
Материал |
№ опыта |
um, % |
uB, % |
ue, % |
Минеральная вата |
1 2 3 4 |
91 91 93 92 |
5 5 5 5 |
4 4 2 3 |
Пенополистирол |
1 2 3 4 |
94 94 94 94 |
5 5 5 5 |
1 1 1 1 |
По результатам расчетов построим диаграммы вкладов составляющих неопределенности в суммарную неопределенность результатов измерений в процентах (%) (см. рисунок А.11 и рисунок А.12).
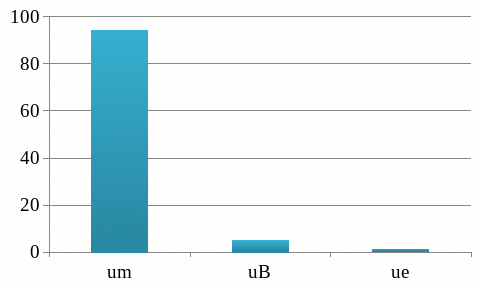
Рисунок А.11 – Диаграмма вкладов составляющих неопределенности в суммарную неопределенность результатов измерений теплопроводности минеральной ваты

Рисунок А.12 – Диаграмма вкладов составляющих неопределенности в суммарную неопределенность результатов измерений теплопроводности пенополистирола
Таким образом, из представленных диаграмм видно, что наибольший вклад в неопределенность результатов измерений теплопроводности вносит составляющая метода «m» (общее среднее значение (математическое ожидание)).

 ,
Вт/(м·К)
,
Вт/(м·К) ,
Вт/(м·К)
,
Вт/(м·К)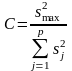 ,
, ,
Вт2/(м·К)2
,
Вт2/(м·К)2 ,
Вт2/(м·К)2
,
Вт2/(м·К)2




 мкВ
мкВ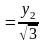 , м
, м , м
, м производится с помощью дисперсионного
анализа
производится с помощью дисперсионного
анализа , С
, С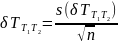 , С
, С производится с помощью дисперсионного
анализа
производится с помощью дисперсионного
анализа
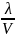









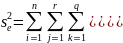



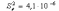
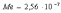







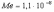

 ,
Вт/(м·К)
,
Вт/(м·К)