Описание неявными функциями

Заключается в моделировании поверхностей в виде:

.

Могут быть использованы функции различных порядков, но из-за сложности математической обработки ограничиваются 1-ой и 2-ой степенью. Поверхности, описываемые функциями 3-ей и 4-ой степени, незначительно расширяют возможности геометрической имитации форм, а вычисления резко увеличиваются.

Поточечное описание

Поверхность представляется множеством отдельных точек, принадлежащих этой поверхности. Теоретически, при бесконечном увеличении числа точек, такая модель обеспечивает непрерывную форму описания.

Поточечное описание применяют в случаях, когда поверхность очень сложна, не обладает гладкостью, а детальное представление многочисленных геометрических особенностей важно. Например, участки грунта на других планетах, формы малых небесных тел, информация о которых доставлена с искусственного спутника в виде нескольких стереопар; микрообъекты, снятые с помощью микроскопов.

Исходная информация представляется в виде матрицы 3-хмерных координат точек. Они определяются автоматизированными методами на стереоприборах. Часто используется сопоставление стереопар. Надо учитывать требуемую частоту расположения точек.

11. Характеристики поверхностей (1-го порядка, 2-го порядка). Поверхности 1-го порядка

Поверхности вида:

в матричном виде имеют вид:

, где .

Изменяя компоненты матрицы Р можно описать плоскость любой ориентации и положения, это будет бесконечная плоскость. Реальный участок имеет ограничения. Наиболее удобно ограничение выпуклым многоугольником. Все другие случаи, как криволинейного ограничения, так и невыпуклой фигурой, могут быть сведены к первому путем аппроксимации или разбиения на выпуклые подфигуры. Рассмотрим крыло самолета.

Граничные точки многоугольника однозначно оцифровывают и записывают их координаты в матрицу:

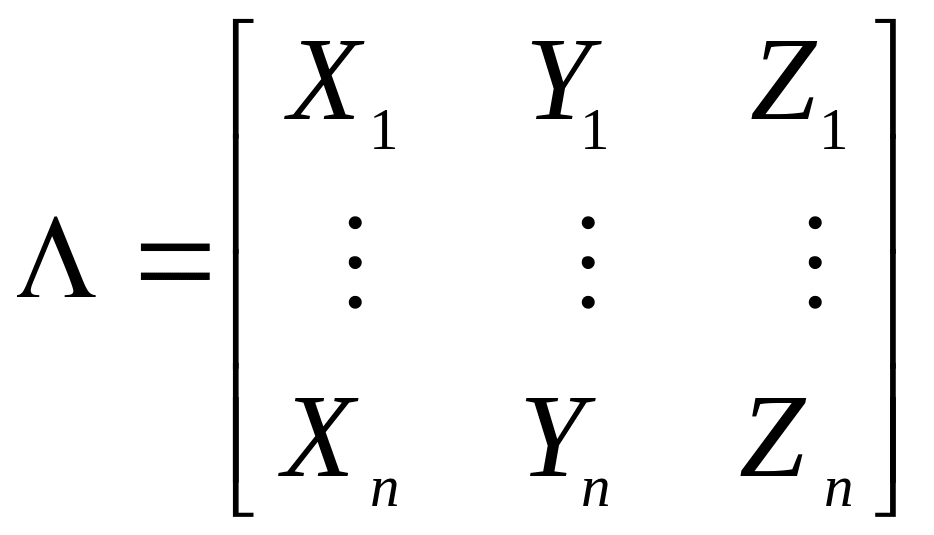, где .

Уравнение плоскости определяют на основе трех точек, не лежащих на одной прямой:

.

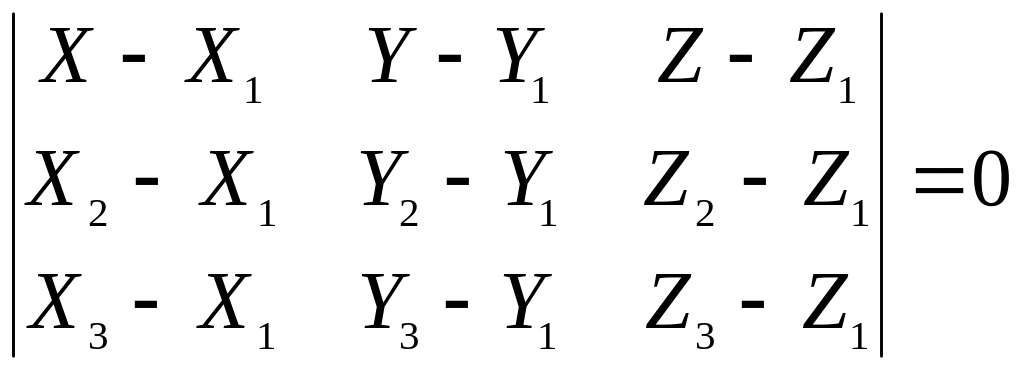Нормаль : .

Направлена нормаль в сторону полупространства, где значение скалярного поля .

Из поверхностей первого порядка составляются полигональные сетки (серия смежных многоугольников, не имеющих разрывов между собой; каждое ребро является общим для смежных многоугольников).

Описывающая функция обладает непрерывностью, а производная имеет разрывы в местах стыка участков.

Достоинства:

— простота обработки.

Поверхности 2-го порядка

Все поверхности кроме эллипсоида бесконечны. Поэтому только эллипсоид может самостоятельно образовывать объемный примитив, все другие требуют ограничения в пространстве.

Квадратичная функция в матричном виде:

, где .

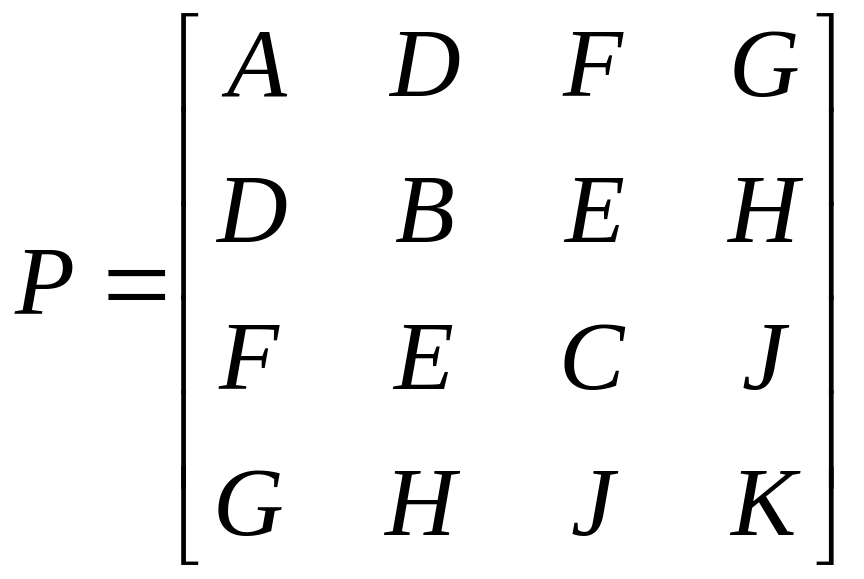Нормаль к поверхности в точке (X,Y,Z) определяется:

, где ,

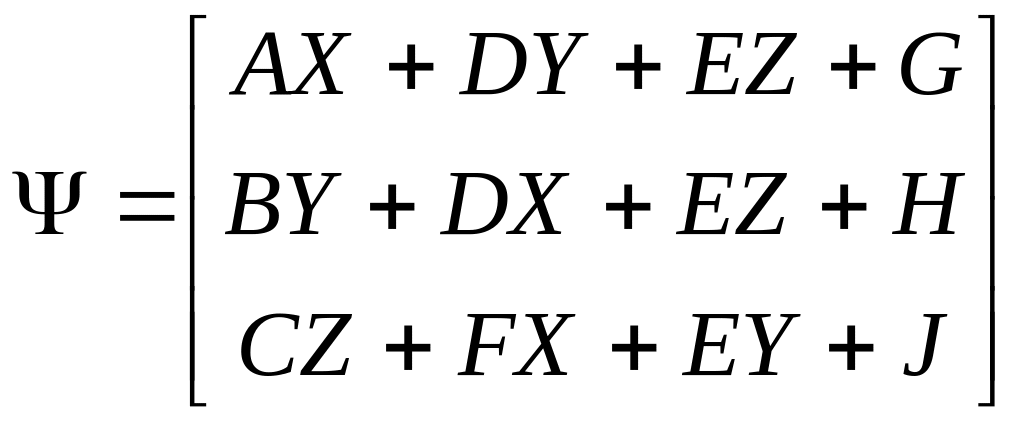i, j, k – орты осей OX,OY,OZ. Направлена нормаль по градиенту скалярного поля , то есть в сторону увеличения значений . Так как функция является монотонной и однократно знакопеременной, то направлена в ту часть подпространства, где . Например, к поверхности шара направлена внутрь шара, а к поверхности того же шара направлена наружу.