30. Метод ранжирования (Саша)

Ранжирование представляет собой процедуру упорядочения объектов, выполняемую лицом, принимающим решение, или экспертом. На основе знаний и опыта лицо, принимающее решение, или эксперт располагают объекты в порядке предпочтения, руководствуясь одним или несколькими выбранными показателями сравнения. В зависимости от вида отношений между объектами возможны различные варианты упорядочения объектов.

Например: пусть среди объектов нет одинаковых по сравниваемым показателям, т.е. нет эквивалентных объектов. В этом случае между объектами существует только отношение строгого порядка. В результате сравнения всех объектов по отношению строгого порядка составляется упорядоченная последовательность, где объект с первым номером является наиболее предпочтительным. Объект со вторым номером менее предпочтителен первому объекту, но предпочтительнее всех остальных объектов и т.д.

31. Схема работы генетического алгоритма (Саша)

Для решения задач функциональной оптимизации в последнее время часто используются адаптивные методы поиска. Представителями таких ме­тодов являются генетические алгоритмы. Адаптивные методы оптимизации основаны на генетических процессах в биологических организмах: биологи­ческие популяции развиваются в течение нескольких поколений, подчиняясь законам естественного отбора и принципу «выживает наиболее приспособ­ленный» (survival of the fittest), открытому Чарльзом Дарвином. Подражая этому процессу, генетические алгоритмы способны «развивать» решения ре­альных задач, если те соответствующим об­разом закодированы. ГА нашли применение в оптимизации, искусственном интеллекте, инженерии знаний и других областях.

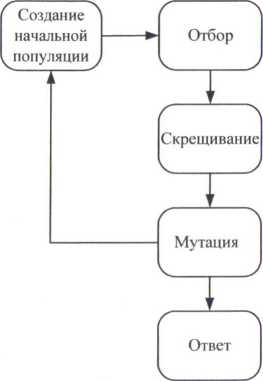
На рис. 2.1 изображена схема работы генетического алгоритма. Вначале генериру­ется (как правило, случайным образом) на­чальная популяция особей (индивидуумов), т. е. некоторый набор решений задачи. Затем моделируется размножение внутри данной популяции. Для этого случайно отбираются несколько пар индивидуумов, производится скрещивание между хромосомами в каждой паре, а полученные новые хромосомы по­мещаются в популяцию нового поколения. В генетическом алгоритме сохраняется ос­новной принцип естественного отбора - чем приспособленное индивидуум (чем больше соответствующее ему значение целевой функции), тем с боль­шей вероятностью он будет участвовать в скрещивании. Далее моделируются мутации - в нескольких случайно выбранных особях нового поколения изме­няются некоторые гены. Затем старая популяция частично или полностью уничтожается и переходят к рассмотрению следующего поколения. Популя­ция следующего поколения в большинстве реализаций генетических алго­ритмов содержит столько же особей, сколько и начальная, но в силу отбора приспособленность в ней в среднем выше. Затем описанные процессы отбо­ра, скрещивания и мутации повторяются уже для этой популяции и т. д.

В каждом следующем поколении будут возникать совершенно новые решения задачи. Среди них как плохие, так и хорошие, но благодаря отбору число хороших решений возрастет. Имитируя эволюцию на компьютере, все­гда сохраняется жизнь лучшему из индивидуумов текущего поколения - та­кая методика называется стратегией элитизма.

Генетический алгоритм работает с некоторой целевой функцией Q(u1,u2,…,un) и в результате находит либо ее максимум, либо минимум (в зависимости от задачи). Алгоритм оперирует набором параметров u1,u2,…,un и находит такое решение, при котором достигается оптимальное значение функции Q. Для организации работы алгоритма не требуется нахо­дить производную от функции Q и выполнять другие вычисления, подразуме­вающие наличие какой-либо алгебраической функции. Другими словами гене­тический алгоритм может работать не только с целевой функцией, но и с ка­ким-либо блоком (набором некоторых действий, операций и вычислений), ко­торый на вход получает некоторый набор значений u1,u2,…,un, а на выходе выдаёт результат, напрямую зависящий от входящих значений.

Работа генетического алгоритма представляет собой итерационный про­цесс, который продолжается до тех пор, пока не выполнится заданное число поколений или какой-либо иной критерий остановки.

Итак, есть некоторая система Q, зависящая от нескольких входных пара­метров u1,u2,…,un, и необходимо найти оптимальный набор вы­ходных параметров у1, у2, • • •, У_т Входные параметры задачи являются гене­тическим материалом - генами. Совокупность генов составляет хромосому. Каждая особь обладает своей хромосомой, а следовательно, своим набором па­раметров. Подав некоторый набор параметров на вход системы Q, можно по­лучить какое-то значение. То, насколько это значение удовлетворяет постав­ленным условиям, определяет характеристику особи, называемую приспособленностью. Функция, определяющая приспособленность, должна удовлетво­рять следующему условию: чем «лучше» особь, тем выше приспособленность.