Лабораторная работа 3.1 построение графика функции
Цель: научиться строить графики от элементарных функций.
Задания и порядок выполнения
Создать таблицу
с использованием математических функций,
которая рассчитывает значение функции
на интервале значений х от 0 до 2, с
шагом 0,1, и построить график функции.
Для этого необходимо:
В ячейку В1 ввести текст «График функции».
В ячейку В3 ввести формулу
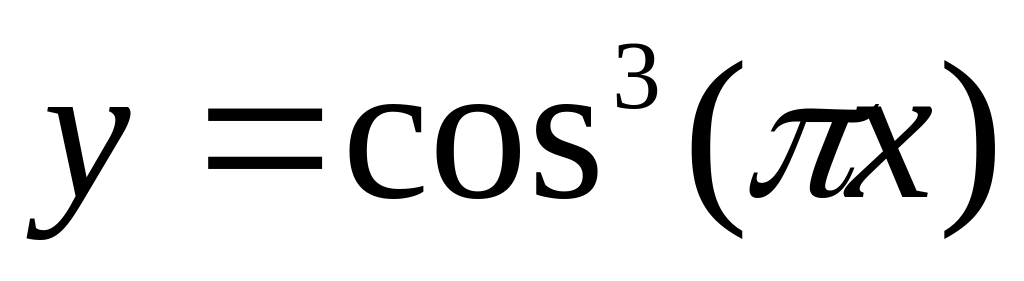.В ячейку А6 ввести текст «Аргумент».
В ячейку В6 ввести текст «Значение функции».
В ячейку А7 ввести начальное значение х: 0.
В ячейку А8 ввести формулу =А7+0.1 для вычисления следующего значения х, изменяющегося с шагом 0.1.
Скопировать формулу из А8 в диапазон А9:А27.
В ячейку В7 ввести формулу расчета значения функции:
=(СOS(ПИ()*А7))^3
Построить график функции с помощью Мастера диаграмм.
Для этого необходимо:
9.1. Выделить диапазон А7:В27.
9.2. Выполнить команду Вставка – Диаграмма.
9.3. На первом шаге Мастера диаграмм выбрать тип графика Точечная и нажать кнопку Далее.
9.4. На втором шаге определить, что данные для построения диаграммы берутся из ряда в столбце и уточнить значения диапазона А7:В27.
9.5. На третьем шаге определить параметры диаграммы: заголовки, подписи данных и т.д.
9.6. На последнем шаге определить положение диаграммы на имеющемся листе и нажать кнопку Готово.
10. Скопировать таблицу на Лист2 и отобразить формулы.
Лабораторная работа 3.2 построение алгебраических и трансцендентных линий на плоскости [7]
Цель: построение алгебраических и трансцендентных линий на плоскости.
Необходимо помнить, что часто различные линии на плоскости задаются в полярных координатах, общее уравнение которых можно записать в виде
,
где , – полярные координаты.
Если линия задана
уравнением
в полярных координатах, то ее уравнение
в декартовых координатах имеет следующий:
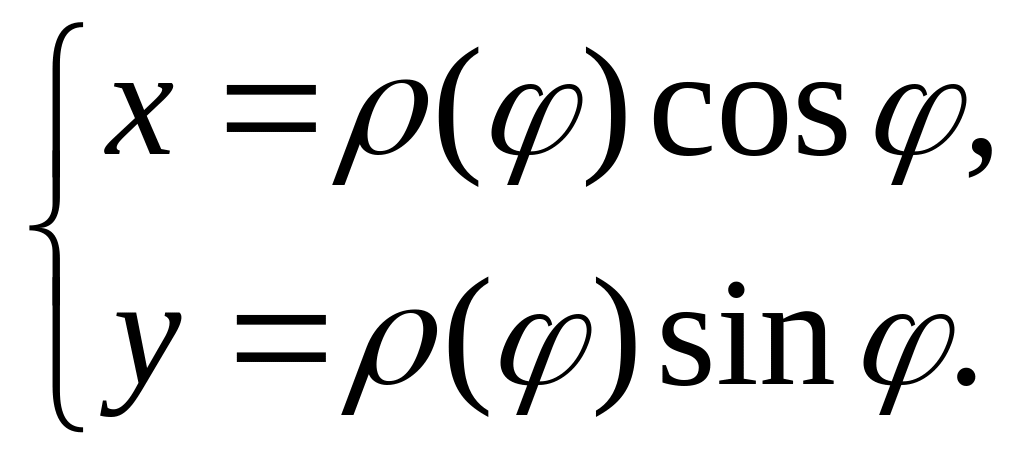(3.1)
Итак, зная уравнение линии в полярных координатах, легко построить график в декартовой системе координат.
Задания и порядок выполнения
Построить функцию,
заданную уравнением в полярных
координатах:
.
Угол изменяется
от 0 до 3,5; шаг изменения 0,05.
Ячейки первого столбца заполнить значениями полярного угла .
В ячейках второго столбца должна содержаться формула расчета полярного угла
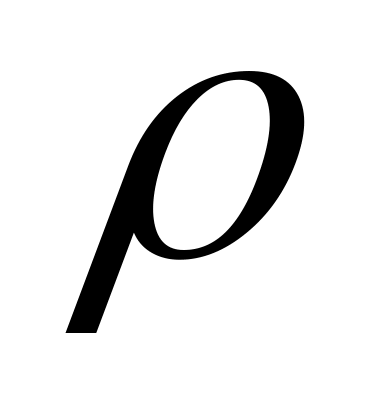(формула
в задании).В ячейках третьего и четвертого столбца должны содержаться расчеты значений функции X, Y из полярных в декартовы координаты – формула (3.1).
Для построения диаграммы выделить значения в столбцах X и Y, затем, используя Мастер диаграмм (тип Точечный), построить и отредактировать диаграмму «Трехлепестковая роза».
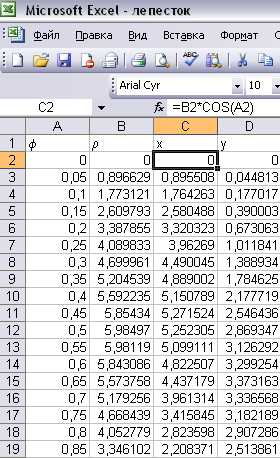
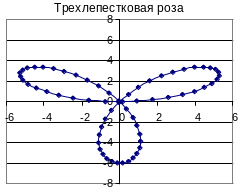
Рис. 3.5. Рассчитанные значения для построения диаграммы трехлепестковой розы |
Рис. 3.6. График трехлепестковой розы
|
Лабораторная работа 3.3 построение поверхностей в ms excel
Цель: построение поверхности в MS Excel.
Необходимо помнить, что работа по построению поверхности предполагает следующую последовательность.
1. Подготовить диапазон изменения функции по двум координатам, расположив изменения одной координаты вдоль некоторого столбца вниз, а другой – вдоль прилегающей строки вправо.
2. Ввести на пересечении координат необходимую формулу для построения поверхности и копировать на всю область построения поверхности. При вводе формул необходимо учитывать смешанные ссылки: по оси Х – столбец не изменяется, по У – строка остается неизменной.
3. Выделить данные и построить диаграмму (тип диаграммы – Поверхность).
4. Отформатировать полученную поверхность.
Задания и порядок выполнения
Построить
поверхность, которая задана уравнением
,
в области
;
шаг 0,2.
Для этого:
Задать в столбце B значения Х в интервале от -1 до 1.
Задать в строке 2 – значения У в интервале от -1 до 1.
Вычислить первое значение поверхности в ячейке В3 по формуле: =($B3^3)/2-(C$2+2)^2, знак «$» перед меткой столбца B и номером строки 2 введен в формулу для того, чтобы ее можно было скопировать в другие ячейки прямоугольного диапазона. После копирования формулы значение X всегда будет вычисляться от значений в столбце B, а значение Y – от значений в строке 2.
Скопировать формулу из ячейки В3 в диапазон С3:К11, заполнив двумерный массив.
Запустить Мастер диаграмм:
5.1. Тип диаграммы Поверхность.
5.2. На втором шаге в качестве меток использовать содержимое ячеек В3:В11.
5.3. Имена каждого ряда заменить числами -1,0, -0,75, …1,0.
5.4. Добавить заголовки осей.
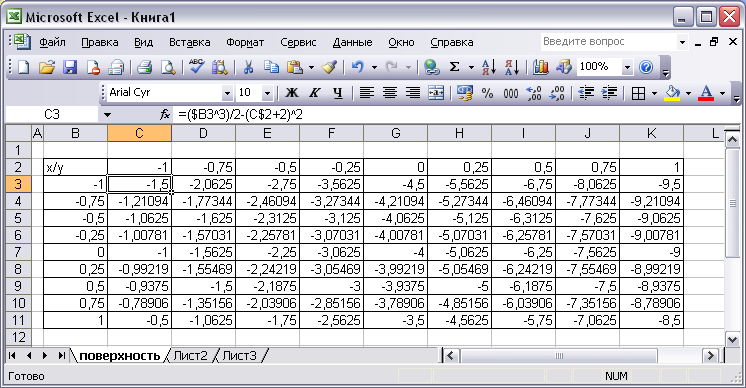
Рис. 3.7. Подготовленный диапазон данных для построения поверхности
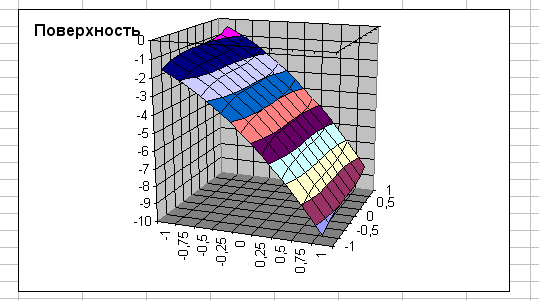
Рис. 3.8. Поверхность