
- •Рекомендации по выполнению курсовой работы
- •Раздел 1. Расчет электрических цепей постоянного тока
- •1.2. Расчет сложных электрических цепей постоянного тока.
- •Раздел 2. Расчет электрических цепей переменного тока
- •Варианты схем однофазных электрических цепей переменного тока
- •2.2 Расчет трехфазных линейных электрических цепей переменного тока
- •Числовые параметры и схемы соединения трехфазных линейных электрических цепей переменного тока
- •Раздел 3. Методика расчёта электрических цепей постоянного и переменного тока.
- •В схеме цепи резисторы r3 и r45 соединены последовательно. Их эквивалентное сопротивление:
- •С хема преобразованной цепи представлена на рис. 3.3:
- •В результате получаем схему цепи (рис. 3.4), в которой резисторы r1 и r2345 соединены последовательно, значит:
- •3.2 Методика расчета сложных электрических цепей постоянного тока.
- •Определить токи и составить баланс мощностей.
- •3.2.1 Метод узловых и контурных уравнений
- •3.2.4 Методика расчета потенциалов точек и построение потенциальной диаграммы
- •3.2.5 Определение напряжения на участках цепи.
- •3.2.6 Методика расчета однофазных линейных электрических цепей переменного тока
- •3.2.7 Методика расчета трехфазных электрических цепей переменного тока
- •3.2.7.1 Методика расчета трехфазных электрических цепей переменного тока при соединении потребителей звездой
- •Графоаналитический метод расчета
- •Символический метод расчета
- •3.2.7.2 Методика расчета трехфазных электрических цепей переменного тока при соединении треугольником
- •Графоаналитический метод расчета
- •Рекомендуемая литература
Символический метод расчета
Строгий аналитический расчет трехфазных цепей производится символическим методом, т. е. в комплексной форме.
Выразим в комплексной форме фазные напряжения:
 B
;
B
;
 =
220
=
220 В
;
В
;
 =
220
=
220 B.
B.
Выразим сопротивления фаз в комплексной форме:
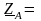 RA
+ jXLA
– jXCA
= 11 + j34
– j53
= (11 – j19)
Ом ;
RA
+ jXLA
– jXCA
= 11 + j34
– j53
= (11 – j19)
Ом ;
 RB
+ jXLB
= (11 + j19)
Ом ;
RB
+ jXLB
= (11 + j19)
Ом ;
 –
jxcc
= (– 22) Ом
–
jxcc
= (– 22) Ом
Переведем комплексные сопротивления фаз из алгебраической формы в показательную.
11
– j19
=
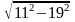
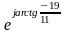 =
22
=
22 Ом ,
Ом ,
где ZA = 22 Ом - полное сопротивление фазы А ;
 -
угол сдвига фаз между током и напряжением
в фазе А.
-
угол сдвига фаз между током и напряжением
в фазе А.
Аналогично определяем:
11 + j19 = 22 Ом,
где
ZB
= 22 Ом ;
 ;
;
– J22
= 22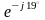 Ом
,
Ом
,
где
ZС
= 22 Ом ,
 90
90
Находим комплексы фазных токов:
 220
220
 =
----- = ---------- = 10
=
----- = ---------- = 10 А
,
А
,
 22
22
модуль
IА
= 10 А, аргумент
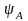 = 60
,
= 60
,
 220
220
 =
----- = ------------ = 10
=
----- = ------------ = 10 А
,
А
,
 22
22
модуль
IВ
= 10 А, аргумент
 = – 180
,
= – 180
,
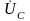 220
220
 =
----- = ------------ = 10
=
----- = ------------ = 10 А
,
А
,
 22
22
модуль
IC
= 10 А, аргумент
 = 210
.
= 210
.
Находим алгебраическую форму записи комплексов фазных токов:
= 10 = 10cos60 + j10sin60 = (5 + j8.66) А ;
= 10 = 10cos(– 180 ) + j10sin(– 180 ) = – 10 А ;
=
10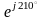 =
10cos210
+ j10sin210
= (– 8.66 – j5)
А
.
=
10cos210
+ j10sin210
= (– 8.66 – j5)
А
.
Вычисляем ток в нейтральном проводе:
 =
+
+
= 5 + j8.66
– 10 – 8.66 - j5
= –13.66 + j3.66
= 14.14
=
+
+
= 5 + j8.66
– 10 – 8.66 - j5
= –13.66 + j3.66
= 14.14 A.
A.
Модуль
IN
=
14.14 А, аргумент
 = 165
.
= 165
.
Вычисляем мощности фаз и всей цепи:
 =
·
=
·
 =
220 · 10
=
2200
=
=
220 · 10
=
2200
=
= 2200 · cos(– 60 ) + j2200 · sin(– 60 ) = (1100 – j1905) B·A ,
где SА = 2200 В·А; PA = 1100 Вт; QA = – 1905 вар;
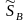 =
·
=
·
 =
220
·10
=
220
·10 =
=
= 2200 = 2200 · cos60 + j2200 · sin60 = (1100 + j1905) B·A,
где SB = 2200 B·А; РB = 1100 Bт; QB = 1905 вар;
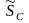 =
·
=
·
 =
220
·10
=
=
220
·10
=
= 2200 = 2200 · cos(– 90 ) + j2200 · sin((– 90 ) = (– j2200) B·A,
где SC = 2200 B·А; РC = 0 Bт; QC = – 2200 вар;
тогда
 =
+
+
= 1100 – j1905 + 1100 + j1905 –j2200 = 2200 – j2200 = 3111
=
+
+
= 1100 – j1905 + 1100 + j1905 –j2200 = 2200 – j2200 = 3111 B·A,
B·A,
где S = 3111 B·A; P = 2200 Bт, Q = – 2200 вар.
3.2.7.2 Методика расчета трехфазных электрических цепей переменного тока при соединении треугольником
В цепи, изображенной на схеме (рис. 3.13), потребители соединены треугольником. Известно линейное напряжение UЛ = 380 В и сопротивления фаз
RAB = 19 Ом, XCAB = 11 Ом, RBC = 12 Ом, XLBC = 16 Ом, RCA = 22 Ом.
Определить фазные, линейные токи, мощности активные, реактивные, полные мощности каждой фазы и всей цепи. Построить векторную диаграмму цепи.
Дано: UЛ = 380 В, RAB = 19 Ом, XCAB = 11 Ом, RBC = 12 Ом, XLBC =16 Ом,
RCA = 22 Ом.
Определить: IА, IB, IC IAB, IBC,. ICA, P, Q, S

Рис. 3.13
