3.2.7 Методика расчета трехфазных электрических цепей переменного тока

3.2.7.1 Методика расчета трехфазных электрических цепей переменного тока при соединении потребителей звездой

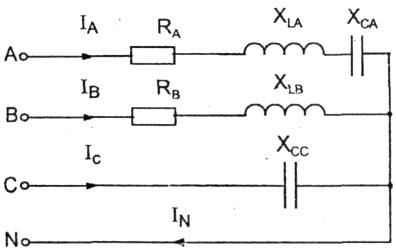
В цепи, изображенной на схеме (рис. 3.11), потребители трехфазно­го тока соединены звездой.

Известно линейное напряжение U_л = 380 В и сопротивления фаз: R_A = 11 Ом, X_LA = 34 Ом, X_CA = 53 Ом, R_B = 11 Ом, Х_LB = 19 Ом, Х_CC = 22 Ом.

Определить полные сопротивления фаз, фазные токи и ток в ней­тральном проводе, активную, реактивную и полную мощности каждой фа­зы и всей цепи.

Дано: U_л = 380 В, R_A = 11 Ом,

X_LA = 34 Ом, X_CA = 53 Ом,

R_B = 11 Ом, Х_LB = 19 Ом,

Х_CC = 22 Ом

Определить: Z_A, Z_B., Z_C,

I_A, I_B, I_C, I_N, P, Q, S

Рис. 3.11

Графоаналитический метод расчета

(расчет с применением векторных диаграмм)

При соединении звездой U_л = U_ф поэтому

U_л 380

U_ф = ---- = ------ = 220 В

Так как есть нейтральный провод, то U_A⁼ U_B= U_С= 220 В.

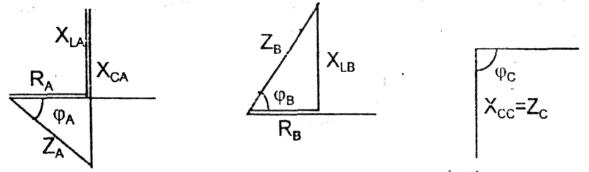
Вычисляем сопротивление фаз и углы φ определяем по диаграм­мам сопротивлений.

Z_A = = 22 Ом

– 19

tgφ_A = -------------- = ------ = – 1.73

R_A 11

φ_A = arctg (– 1.73) = – 60 - в фазе А напряжение отстает от тока на 60 .

Z_B = = = 22 Ом

X_LB 19

tgφ_B = ------ = ----- = 1.73

R_B 11

φ_B = arctg1.73 = 60 - в фазе В напряжение опережает ток на 60

Z_C = Х_CC = 22 Ом

φ_B = – 90 - в фазе С напряжение отстает от тока на 90 ,

т. к. в цепь включен конденсатор.

Фазные токи можно определить следующим образом:

U_A 220

I_A = ----- = ------ = 10 A ; φ_A = – 60 ;

Z_A 22

U_B 220

I_B = ----- = ------ = 10 A ; φ_B = 60 ;

Z_B 22

U_C 220

I_C = ----- = ------ = 10 A ; φ_C = – 90 .

Z_C 22

Чтобы вычислить ток в нейтральном проводе, нужно построить векторную диаграмму цепи. На векторной диаграмме под утлом 120 друг относительно друга строятся векторы фазных напряжений одинаковой длины.

Векторы фазных токов строятся в масштабе под вычисленными уг­лами φ по отношению к фазным напряжениям.

В фазе А нагрузка носит емкостный характер, значит,

ток I_A опережает напряжение U_A на угол φ_A .

В фазе В нагрузка носит индуктивный характер, следовательно,

ток I_В отстает от напряжения U_B на угол φ_B .

В фазе С нагрузка емкостная, следовательно,

ток I_C опережает на­пряжение U_C на угол φ_C = 90 . М₁ = 2.5 А/см - масштаб.

I_A 10

1_IA = --- = ---- = 4 см.

M₁ 2.5

I_B 10

1_IB = --- = ---- = 4 см.

M₁ 2.5

I_C 10

1_IС = --- = ---- = 4 см.

M₁ 2.5

Ток в нейтральном проводе равен геометрической (векторной) сумме фазных токов:

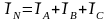
Измерив длину вектора 1_IN , находим tok I_N = 1_IN ∙ M₁,

I_N = 5.7 ∙ 2.5 = 14.25 А.

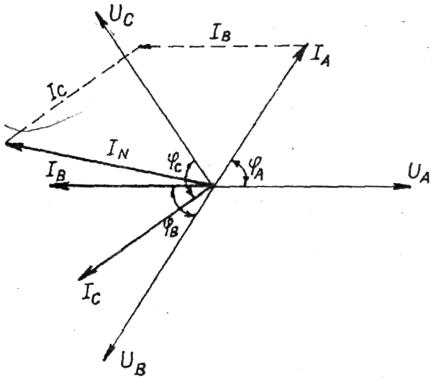
Рис. 3.12

Определим активные мощности фаз:

P_A = U_A ∙ I_А ∙ соsφ_A = 220 ∙ 10 ∙ cos(–60 ) = 1100 Вт,

Р_B = U_B ∙ I_B ∙ соsφ_B = 220 ∙ 10 ∙ cos60 = 1100 Вт,

P_C = U_C ∙ I_C ∙ сosφ_C = 220 ∙ 10 ∙ cos(–90 ) = 0 Вт.

Активная мощность трехфазной цепи:

Р = Р_А + Р_В+ Р_C = 1100 + 1100 = 2200 Вт

Определяем реактивные мощности фаз:

Q_A = U_A ∙ I_A ∙ sinφ_A = 220 ∙ 10 ∙ sin(–60 ) = –1905 вар,

Q_B = U_B ∙ I_B ∙ sinφ_B = 220 ∙ 10 ∙ sin60 = 1905 вар,

Q_C = U_C ∙ I_C ∙ sinφ_C = 220 ∙ 10 ∙ sin(–90 ) = –2200 вар.

Реактивная мощность трехфазной цепи:

Q = qa + qb + Qc = - 2200 вар

Вычисляем полную мощность каждой фазы и всей цели:

S_A = U_A ∙ I_A = 220 ∙ 10 = 2200 B∙A;

S_B = U_B ∙ I_B = 220 ∙ 10 = 2200 B∙A;

S_C = U_C ∙ I_C = 220 ∙ 10 = 2200 B∙A;

S = 3111 B∙A