3.2.4 Методика расчета потенциалов точек и построение потенциальной диаграммы

Выберем контур, включающий две эдс.

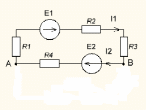рис. 3.8

Зададимся обходом контура по часовой стрелке. Заземлим одну из точек контура, пусть это будет точка А. Потенциал этой точки равен нулю: φА=0. Зная величину и направление токов ветвей и эдс, а также величины сопротивлений, вычислим потенциалы всех точек контура при переходе от элемента к элементу.

φС= φА I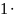 R1 =0- 0.89·15=−13.35 В

φD= φС + E1− I ∙ r01 = −13.35+40−0.89∙ 1=25.76 В

φF= φD − I R2 = 25.76− 0.89∙ 27= 1.73 В

φB= φF − I R3 = 1.73− 0.89∙ 5=−2.72 В

φG= φB + E2− I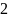 ∙ r02 =−2.72+20− 1∙ 2= 15.28 В

φA= φG – I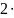 R4 = 15.28 −1∙ 15=0.28≈ 0 – проверочная точка.

Строим потенциальную диаграмму. По оси абсцисс откладываем сопротивление контура в той последовательности, в которой производим обход контура, прикладывая сопротивления друг к другу, по оси ординат- потенциалы точек с учетом их знака.

3.2.5 Определение напряжения на участках цепи.

Напряжение между двумя точками электрического поля равно разности потенциалов поля в этих точках. С помощью потенциалов точек определим напряжения UАВ и UCG:

UАВ = φА – φB = 0−(− 2.72)= 2.72 В

UCG = φG – φС =15.28−(−13.35)=28.63 В

3.2.6 Методика расчета однофазных линейных электрических цепей переменного тока

К зажимам электрической цепи, схема замещения которой приведе­на на рис. 2.35, подключен источник синусоидального напряжения u = 311 ∙ sin(ωt + 45°) В частотой f = 50 Гц.

Параметры элементов схемы замещения: R₁ = 5 Ом, R₂ = 8 Ом,

L₁ = 39,8 мГн, L₂ = 19 мГн, С₁ = 162,5 мкФ, С₂ = 192 мкФ.

Выполнить следующее:

1) определить реактивные сопротивления элементов цепи;

2) определить действующие значения токов во всех ветвях цепи;

3) записать уравнение мгновенного значения тока источника;

4) составить баланс активных и реактивных мощностей;

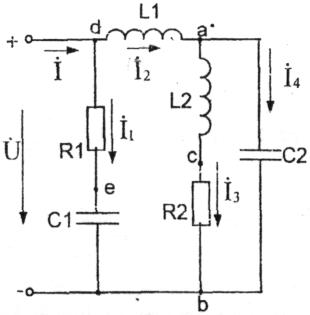
Дано: R₁ = 5 Ом, R₂ = 8 Ом

L₁ = 39,8 мГн, L₂ = 19 мГн

С₁ = 162,5мкФ,С₂=192мкФ

Определить: X_L1, X_L2, X_C1, X_C2,

I, I₁, I₂, I₃, I₄, i

Рис. 3.9

Реактивные сопротивления элементов цепи:

X_L1 = ωL₁ = 2πfL₁ = 314∙39,8∙10^-3 = 12,5 Ом;

X_L2 = ωL₂ = 2πfL₂ = 314∙19∙10^-3 = 6 Ом;

1 1 1∙10⁶

X_C1 = ------ = ------- = ------------- = 19,6 Ом

ωC₁ 2πfC₁ 314∙162,5

1 1 1∙10⁶

X_C2 = ------ = ------- = ----------- = 16,6 Ом

ωC₂ 2πfC₂ 314∙192

Расчет токов в ветвях цепи выполняем методом эквивалентных преобразований.

Представим схему, приведенную на рис. 3.9, в следующем виде:

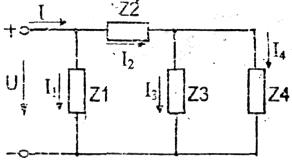
Рис 3.10

Находим комплексные сопротивления ветвей, затем участков цепи и всей цепи:

₁ = R₁ – jX_С1 = 5 – j ∙ ∙ = 20.2 ∙ Ом;

₂ = jX_L1 = j12.5 = 12.5 Ом;

₃ = R₂ + jX_1.2 = 8 + j6 = 10 Ом;

₄ = – jX_C2 = – j16.6 = 16.6 Ом;

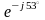₃ ∙ ₄ 10 ∙ 16.6 166 166

_{3 4} = ----------- = ----------------------- = ------------ = ------------ = 12.5 Ом;

₃ + ₄ 8 + j6 – j16.6 8 – j10.6 13.3

_{2 3 4} = ₂ + _{3 4} = j12.5 + 12.5 = 17.7 Ом;

₁ ∙ _{2 3 4} 20.2 ∙ 17.7 357.54 357.54

_экв = ------------- = --------------------------- = ---------------- = ---------------- =

₁ + _{2 3 4} 5 – j19.6 + j12.5 + 12.5 17.5 – j7.1 18.92

18.92 Ом

Выразим действующее значение напряжений в комплексной форме:

U_м 311

= ----- = ----- = 220 B

Вычисляем токи ветвей и общий ток цепи:

220

₁ = ----- = -------------- = 10.9 A;

₁ 20.2

220

₂ = -------- = ------------ = 12.4 A;

_{2 3 4} 17.7

220

= ------- = -------------- = 11.62 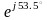A или

_экв 18.92

= ₁ + ₂ =10.9 +12.4=10.9 ∙ cos +j10.9 ∙ sin +12.4=6.85+j9.4 = 11.6 A

Для определения токов параллельных ветвей I₃ и I₄ рассчитаем напряжение на зажимах этих ветвей.

_ab = _{3 4} = ₂ ∙ _{3 4} = 12.4 ∙ 12.5 = 155 B;

_ab 155

₃ = ----- = --------- = 15.5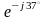 A;

₃ 10

_ab 155

₄ = ----- = ----------- = 9.35 A

₄ 16.6

3) Уравнение мгновенного значения тока источника:

i = I_M sin(ωt + ψ_j)

i = 11.6 sin(ωt + 54 ) = 16.3sin(314t + 54 ) A

4) Комплексная мощность цепи:

­­

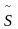= I* = 220 ^{­­­­­­∙} 11.6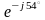 = 2550 = 2510 – J400 B∙A;

где S_ист = 2550 B∙A,

P_ист = 2550 Вт,

Q_ист = – 400 вар (знак минус определяет емкостный характер нагрузки в целом).

Активная Р_пр и реактивная Q_пр мощности приемников:

Р_пр = I₁² R₁ + I₃² R₂ = 10.9² ∙ 5 + 15,5² ∙ 8 = 2510 Вт;

Q_пр = I₁²(–x_C1)+I₂²(x_L1)+I₃²(x_L2)+I₄²(–x_C2) =

= 10.9² ∙(–19.6)+12.4² ∙12.5+15.5² ∙ 6+9.35² ∙(–16,6) = – 400 вар.

Баланс мощностей выполняется:

P_ист = Р_пр; Q_ист = Q_пр

или в комплексной форме:

= ₁ + ₂ + ₃ + ₄ = _{1 1} + _{2 2} + _{3 3} + _{4 4} ;

где ₂ = ₂ ∙ ₂ = 12.4 ∙ j12.5 = j155 B = 155 B;

₃ = ₄ = _{3 4}

2510 – j400 = 220 ∙ 10.9 + 155 ∙ 12.4 + 155 ∙ 15.5 + 155 ∙ 9.35 ;

2510 – j400 = 596.4 – j2322.7 + 1922 + 1918.7 + j1449.3;

2510 – j400 = 2515 – j403.9 - баланс практически сходится.