
- •Рекомендации по выполнению курсовой работы
- •Раздел 1. Расчет электрических цепей постоянного тока
- •1.2. Расчет сложных электрических цепей постоянного тока.
- •Раздел 2. Расчет электрических цепей переменного тока
- •Варианты схем однофазных электрических цепей переменного тока
- •2.2 Расчет трехфазных линейных электрических цепей переменного тока
- •Числовые параметры и схемы соединения трехфазных линейных электрических цепей переменного тока
- •Раздел 3. Методика расчёта электрических цепей постоянного и переменного тока.
- •В схеме цепи резисторы r3 и r45 соединены последовательно. Их эквивалентное сопротивление:
- •С хема преобразованной цепи представлена на рис. 3.3:
- •В результате получаем схему цепи (рис. 3.4), в которой резисторы r1 и r2345 соединены последовательно, значит:
- •3.2 Методика расчета сложных электрических цепей постоянного тока.
- •Определить токи и составить баланс мощностей.
- •3.2.1 Метод узловых и контурных уравнений
- •3.2.4 Методика расчета потенциалов точек и построение потенциальной диаграммы
- •3.2.5 Определение напряжения на участках цепи.
- •3.2.6 Методика расчета однофазных линейных электрических цепей переменного тока
- •3.2.7 Методика расчета трехфазных электрических цепей переменного тока
- •3.2.7.1 Методика расчета трехфазных электрических цепей переменного тока при соединении потребителей звездой
- •Графоаналитический метод расчета
- •Символический метод расчета
- •3.2.7.2 Методика расчета трехфазных электрических цепей переменного тока при соединении треугольником
- •Графоаналитический метод расчета
- •Рекомендуемая литература
Раздел 3. Методика расчёта электрических цепей постоянного и переменного тока.
3.1 Методика расчета электрических цепей постоянного тока
В схеме электрической цепи (рис. 3.1) E = 140B, R1 = 10 Ом, R2 = 100 Ом,
R 3
= 30 Ом, R4
= 300 Ом, R5
= 200 Ом, r=2
Ом.
3
= 30 Ом, R4
= 300 Ом, R5
= 200 Ом, r=2
Ом.
Рис. 3.1
Определить токи в ветвях цепи, составить баланс мощностей.
Решение.
3.1.1. Укажем направления токов в ветвях в соответствии с направлением ЭДС.
3.1.2. Определим эквивалентное сопротивление цепи методом «свертывания».
Резисторы R4 и R5 соединены параллельно, поэтому их эквивалентное сопротивление: R45 = R4R5 /R4+R5 = 300∙200/500 = 120 Ом
П осле
преобразования схема имеет вид (3.2)
осле
преобразования схема имеет вид (3.2)
Рис. 3.2
В схеме цепи резисторы r3 и r45 соединены последовательно. Их эквивалентное сопротивление:
R345 = R3 +R45 = 150 Ом.
С хема преобразованной цепи представлена на рис. 3.3:
Рис. 3.3
Так как резисторы R2 и R345 соединены параллельно, то их эквивалентное сопротивление:
R45 = R2 R345 /R2 R345 =100*150/250 = 60 Ом.
В результате получаем схему цепи (рис. 3.4), в которой резисторы r1 и r2345 соединены последовательно, значит:
Rэк
= R1+
R2345
= 10+60 = 70 Ом.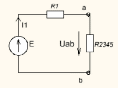
Рис. 3.4
3.1.3 Определяем токи в ветвях электрической цепи.
По закону Ома для полной цепи находим общий ток (рис.3.4)
I1 =E/Rэк+ r = = 140/72 = 1.944 A.
Для определения других токов находим падение напряжения на участках цепи. В соответствии со схемой цепи (рис. 3.4) из закона Ома для участка цепи напряжение
Uab = I1∙ R2345 = 1.944∙60 = 116.64 B.
Тогда токи в параллельных ветвях (рис. 3.3)
I2 = Uab/R2 = 116.64/100 =1,17 A, I3 = Uab/R345 = 116.64/150 = 0,78 A.
Аналогично для схемы цепи (рис.3.2) определим напряжение:
Ucd = I3 ∙R45 = 0,78∙120 = 93.6 B.
Ток в параллельных ветвях:
I4 = Ucd/R4 = 93.6/300 =0,312 A, I5 = Ucd/R5 = 93.6/200 = 0,468 A.
3.1.4 Составим баланс мощностей:
Мощность источника энергии:
Pист = EI1 = 140∙1.944 = 272.16 Вт.
Мощность приёмника энергии рассчитываем по закону Джоуля-Ленца:
P=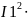 R1+
R1+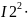 R2+
R2+ R3+
R3+ R4+
R4+ R5
R5
1.944∙1.944∙10+1,17∙1.17∙100+0,78∙0.78∙30 +0,312∙0.312∙300 +0,48∙0.48∙200
= 265.2 Вт
Мощность потерь: P0= r =1.944∙1.944∙2=7.56 Вт
Подставим числовые значения в уравнение баланса мощностей:
Pист = Pпр+ P0,
272.16=265.2+7.56,
272.16≈272.76
Баланс мощностей соблюдается, следовательно, токи определены правильно.
3.2 Методика расчета сложных электрических цепей постоянного тока.

Рис. 3.5
В электрической цепи: Е1 = 40В, Е2 = 20В, R1 = 15 Ом, R2 = 27 Ом, R3 = 5 Ом,
R4 = 15 Ом, R5 = 12 Ом, R6 = 10 Ом, R7 = 5 Ом, r01 = 1 Ом, r02=2 Ом
Определить токи и составить баланс мощностей.
3.2.1 Метод узловых и контурных уравнений
Выбираем произвольно направления токов в ветвях (рис.3.5) и
составляем систему уравнений по законам Кирхгофа для определения
токов в ветвях. Так как в схеме три ветви, то необходимо составить три
уравнения: по первому закону Кирхгофа – одно уравнение (на единицу
меньше числа узлов) и по второму закону Кирхгофа недостающее число
уравнений, т.е. два уравнения.
Система уравнений для расчёта токов имеет вид:
I1 – I2 – I3 = 0 (для узла В) (1)
E1+E2 = I1∙ (R1+r01+R2+R3) + I2∙ (R4+r02) (2)
-E2 = -I2∙ (R4+r02) + I3∙ (R5+R6+R7) (3)
Решая полученную систему уравнений, найдём токи в ветвях. Подставим значения ЭДС и сопротивлений:
I1 – I2 – I3 = 0
40+20 = I1 ∙ (15+1+27+5) +I2 ∙ (2+15)
-20 = -I2 ∙ (15+2) + I3 ∙ (12+10+5)
∙
I1 – I2 – I3 = 0 (4)
60
= I1 48+I2
17
(5)
48+I2
17
(5)
-20 =-I2 17+I3 ∙27 (6)
Выразим I1 из (5) -го уравнения, I3 из (6) -го уравнения
I1 – I2 – I3 = 0
48 ∙I1 = 60 – 17 ∙I2
27 ∙I3 = -20+17∙ I2
I1 – I2 – I3 = 0
I1
=
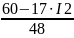 =
=
 –
–
 I2
= 1,25 – 0,35 ∙I2
(7)
I2
= 1,25 – 0,35 ∙I2
(7)
I3
=
 =
=
 +
+ =
-0,74+0,63∙ I2
(8)
=
-0,74+0,63∙ I2
(8)
Подставим полученные значения I1 и I3 в (4)-е уравнение:
(1,25 – 0,35 ∙I2) – I2 – (-0,74+0,63∙ I2) = 0
1,25 – 0,35 ∙I2 – I2+0,74 – 0,63 ∙I2 = 0
-0,35 ∙I2 – I2 – 0,63 ∙I2 = -0,74 – 1,25
-1,98 ∙I2 = -1,99
I2 = -1,99 / -1,98 1А
Подставим найденное значение тока I2 в уравнение (7) и (8), и определим токи I1 и
I3:
I1 = 1,25 – 0,35 ∙I2 = 1,25 – 0,35 1 =0,9 A
I3 = -0,74+0,63∙ I2 = -0,74+0,63 1 = -0,11
3.2.2 Метод контурных токов.
Считаем, что в каждом независимом контуре схемы (рис 3.5) течёт свой контурный ток Iк1, Iк2. Выбираем направления токов в одну сторону, по часовой стрелке.
Составляем уравнения по второму закону Кирхгофа относительно контурных токов. Направление обхода контуров примем совпадающими с направлением контурных токов. Определим контурные ЭДС:
EI = E1+E2 = 40+20 = 60 B
EII = -E2 = -20B
Это алгебраическая сумма ЭДС, входящих в контур.
Определим собственные сопротивления контуров:
RI = R1+R2+R3+R4+r01+r02 = 15+27+5+15+1+2 = 65 Ом
RII = R4+R5+R6+R7+r02 = 15+12+10+5+2 = 44 Ом
Оно определяется как алгебраическая сумма всех сопротивлений, входящих в контур.
Общим для контуров является сопротивление (R4+r02).
Составим систему уравнений:
EI = Iк1 RI – Iк2 (R4+r02) (9)
EII = Iк2 RII – Iк1 (R4+r02) (10)
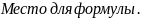
В уравнении (9) слагаемое Iк2∙(R4+r02) записывается со знаком минус, так как из-за второго контурного тока на общих сопротивлениях (R4+r02) создаётся падение напряжения, причём направление токов Iк2 и Iк1 на этих сопротивления не совпадают.
Аналогично в уравнении (10) из-за тока Iк1 создаётся падение напряжения на общих сопротивлениях (R4+r02).
Подставим известные значения сопротивлений и ЭДС:
60 = Iк1 65 - Iк2 (15+2)
-20 = Iк2 44 – Iк1 15+2)
60 = Iк1 65 - Iк2 17 (11)
-20 = Iк2 44 – Iк1 17 (12)
выразим из (11)-го уравнения Iк1
65 ∙Iк1 = 60 + 17∙Iк2
-20 = 44∙Iк2 – 17∙ Iк1
Iк1
=
 =
=
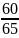 +
+ =
0,92+0,26 ∙Iк2
=
0,92+0,26 ∙Iк2
-20 = 44 ∙Iк2 – 17∙Iк1
и подставим его значения в (12)-ое уравнение:
-20 = 44 ∙IК2 – 17∙(0,92+0,26 ∙IK2)
-20 = 44 ∙IK2 – 15,64 – 4,42 ∙I K2
-20+15,64 = 44 ∙IK2 – 4,42∙ IK2
-4,36 = 39,58 ∙IK2
IK2 = -4,36 / 39,58 = -0,11 A
Из уравнения (13) определим IK1:
IK1 = 0,92+0,26 ∙IK2 = 0,92+0,26 ∙(-0,11) = 0,89 A
Определяем действительные токи в ветвях.
Ток в ветви равен алгебраической сумме контурных токов, протекающих в зтой же ветви.
Рассчитываем значения токов в ветвях схемы (рис. 3.5), сравнивая направления контурных токов в ветвях с направлением действующих токов:
I1 = IK1 = 0,89 A
I2 = IK1 – IK2 =0,95 – (-0,11) = 1,1 A
I3 = IK2 =-0,11 A
3. 2.3. Метод наложения токов.
При решении этим методом из схемы поочерёдно исключаем по одному источнику ЭДС. Тогда схема решается как простая схема с одним источником ЭДС и смешанным соединением сопротивлений. Токи в такой схеме называются частичными. Исключаем из схемы источник Е1:

Рисунок 3.6
Вычислим эквивалентное сопротивление цепи:
R123,r02 = R1+R2+R3+r02 = 15+27+5+2 = 49 Ом
R123567,r02 =( R123,r02 R567) /( R123,r02+R567) = (49 27) / (49+27) = 1323 / 76 = 17,41 Ом
R = R123567,r02+R4 = 17,41+15 = 32,41 Ом
По закону Ома для полной цепи, общий для данной схемы ток I2’
определяется:
I2’ = E2 /( R+r02) = 20 /( 32,41+2) = 0,58 A
Для определения токов I1’ и I3’ найдём падение напряжения на участке АВ.
UAB = I2’ R123567,r02 = 0,58 17,41 = 10,1 B
I1’ = UAB / R123,r02 = 10,1 / 49 = 0,21 A
I3’ = UAB / R567 = 10,1 / 27 = 0,37 A
И сключим
из схемы источник Е2:
сключим
из схемы источник Е2:
Рисунок 3.7
Вычислим эквивалентное сопротивление цепи:
R567 = R5+R6+R7 = 12+10+5 = 27 Ом
R4,r02 = R4+r02 = 15+2 = 17 Ом
R4567,r02 =( R567 R4,r02) / (R567+R4,r02) =( 27 17) /( 27+17) = 459/44 = 10,43 Ом
R = R4567,r02+R1+R2+R3= 10,43+15+27+5 = 57,43 Ом
По закону Ома для полной цепи общий для данной схемы I1’’ определиться:
I1’’ = E1/(R+r01) = 40/(57,43+1) = 0,68 A
Для определения токов I2’’ и I3’’ найдём падение напряжения на участке СД:
UСД = I1’’ ∙R4567,r02 = 0,68∙10,43 = 7,09 B
I2’’ = UСД/R4,r02 = 7,09/17 = 0,42 A
I3’’ = UСД/R567 = 7,09/27 = 0,26 A
Вычислим действительные токи в ветвях наложением частичных токов с учётом их направления:
I1 = I1’+I1’’ = 0,21+0,68 = 0,89 A
I2 = I2’+I2’’ = 0,58+0,42 = 1 A
I3 = I3’ – I3’’ = 0,26 – 0,37 = -0,11 A
Действительное направление тока I3 противоположно заданному (об этом свидетельствует знак “минус”)
2.4 Составим баланс мощностей
На основании закона сохранения энергии количество теплоты, выделяющееся в единицу времени в сопротивлениях цепи, должно равняться энергии, доставляемой за то же время источниками питания.
Уравнение баланса мощностей: Pи = Pп+Pо
где Pи = Е∙I – мощность источника энергии; Pп = I2∙R– мощность потребителя
энергии;
Pо = I2 r – мощность потерь.
В нашем случае:
Pи = E1 I1+E2 I2 = 40 0,89+20 1 = 35,6+20 = 55,6 Вт
Pп = I1 I1(R1+R2+R3) + I2 I2 R4+I3 I3 (R5+R6+R7) = 0,89 0,89 (15+27+5) +
+1 1 15+(-0,11) (-0,11) 12+10+5) = 0,79 47+15+0,012 27 = 37,13+15+0,324 = 52,45 Вт
Pо = I1 I1 r01+I2 I2 r02 = 0,89 0,89 1+1 1 2 = 0,79+2 = 2,79 Вт
55,6 = 52,45+2,79
55,6 = 55,24
Расхождение в результатах вычислений не превышают 1%, это означает, что токи рассчитаны правильно.
