9.3. Общий индекс как средняя величина индивидуальных индексов

Общий индекс можно получить как среднее значение соответствующих индивидуальных индексов. В этом смысле общим индексом отражаются результаты изменения уровня явления у отдельных единиц совокупности. При расчете общего индекса как средней величины веса индивидуальных индексов подбираются так, чтобы был возможен алгебраический переход от общего индекса в форме средней величины к общему индексу в агрегатной форме¹⁴. Эти преобразования, как правило, не сложны. Например, индекс общего объема товарооборота можно представить средней арифметической величиной -

.

Тот же индекс может быть записан в форме средней гармонической величины.

.

Индекс изменения общей суммы товарооборота в связи с изменением количества проданных товаров (индекс физического объема – I_q) можно представить как

(В форме средней гармонической индекс физического объема практически не используется).

Индекс изменения общей суммы товарооборота в связи с изменением цен на товары (I_p) можно представить средней гармонической величиной:

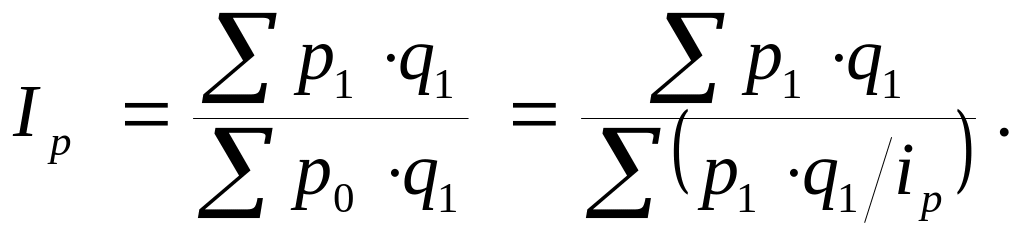
9.4. Индексный метод анализа итогового показателя и структурных изменений

Показанные выше общие индексы в агрегатной форме либо в форме средней величины позволяют оценить вклад отдельных факторов (например, изменение объема продаж и цены товаров, объема кредитных услуг и процентной ставки и т.п.) в общий прирост итогового показателя. Методика индексного анализа изменения итогового показателя (изменения общей суммы выручки от реализации, прироста общей суммы дохода от предоставления кредитных услуг разного типа и т.д.) применима при анализе совокупностей, состоящих как из разных объектов, так и из объектов одного и того же типа.

Если совокупность неоднородна (например, совокупность товаров различного вида), то индекс физического объема – единственный способ показать динамику такой массы различных предметов, выражая ее через взвешивающий множитель (цену, себестоимость, трудоемкость), а агрегатный индекс качественного показателя, например, агрегатный индекс цен – это единственный способ оценить общее изменение уровня качественного признака, например, общее изменение цен.

Если же совокупность состоит из объектов одного типа, то динамику этой массы можно показать непосредственным сравнением общего количества таких предметов в отчетном периоде с аналогичным значением в базисном периоде. Так, при анализе изменения валового дохода банка можно определить индекс общего объема кредитных услуг как отношение суммы кредитных услуг банка (объема среднегодовой задолженности) в отчетном периоде к соответствующей сумме в базисном периоде –

I_K = K₁ / K₀,

а также индекс физического объема кредитных услуг, показывающий, во сколько раз изменилась общая сумма дохода банка за счет изменения объема по отдельным видам предоставляемого кредита –

Рассмотрим пример движения валового дохода коммерческого банка в зависимости от изменения среднегодовой задолженности по кредитам (количественный фактор – K) и процентной ставки за кредит (качественный фактор – S). Исходные данные приведены в таблице

Виды кредитов	Базисный период		Отчетный период
	Среднегодовая задолженность (K0), млн. руб.	Средняя процентная ставка (S0), %	Среднегодовая задолженность (K0), млн. руб.	Средняя процентная ставка (S0), %
1. Краткосрочные	665,5	4,7032306	702,0	4,8290598
2. Долгосрочные	169,5	1,7286135	298,0	1,8020134
Итого	835,0	4,0994011	1000,0	3,927

Валовой доход от реализации кредита составлял:

в базисном году – ВД0 = К0·S0 = 34,23 млн. руб.,

в отчетном году - ВД1 =К1·S1 = 39,27 млн. руб.

Прирост валового дохода (ВД1 - ВД0) = 5,04 млн. руб.

Условная величина дохода от предоставления кредитных услуг в отчетном периоде при базисной процентной ставке была бы равна К1·S0 = 38,168 млн. руб.

Индекс общего объема кредитных услуг равен

IK = K1 / K0 = 1000/835 = 1,1976047.

Индекс физического объема кредитных услуг равен

.

Индекс изменения величины процентной ставки за кредит равен

.

Таким образом, прирост валового дохода объясняется

а) изменением объема кредитных услуг Д(К) = 34,230–(1,1150437–1) = 3,938 млн. руб.;

б) изменением процентной ставки Д(S) = 34,230–1,1150437–(1,0288737–1) = 1,102 млн. руб.

Более детальный анализ изменения итогового показателя возможен при изучении так называемых структурных сдвигов и их влияния на прирост итогового показателя (продукции, валового дохода, общих затрат на производство и т.д.).

Рассмотрим соотношение между индексами физического объема (I_K) и общего объема (I_K). В формуле I_K разделим и умножим числитель на K₁ а знаменатель – на K₀. Получим

Таким образом, для однородных совокупностей (допускающих суммирование по количественному признаку) индекс физического объема есть произведение индекса общего объема совокупности на индекс, выражающий изменение структуры совокупности (в данном случае – это изменение удельного веса отдельных видов кредитных услуг в общей их сумме).

Формула индекса структурных изменений для нашего примера:

,

где d₀ – удельные веса, доли отдельных видов кредитных услуг в общем их объеме в базисном периоде, а d₁ – удельные веса или доли отдельных видов кредитных услуг в общем их объеме в отчетном периоде:

d₀ = K₀ / K₀, d₁ = K₁ / K₁.

Знаменатель в формуле индекса структурных изменений в нашем примере есть не что иное, как средний размер процентной ставки по всем видам кредитов в базисном периоде, так как .

Экономическая сущность индекса структурных изменений в том, что он показывает влияние процессов перераспределения на общий прирост итогового показателя. В той же мере этот индекс показывает, во сколько раз изменился общий средний уровень качественного показателя (средней процентной ставки, средней цены, среднего уровня оплаты труда и т.п.) только за счет изменения удельного веса каждого объекта в общем объеме количественного признака.

При известных значениях I_K и I_K, влияние структурных сдвигов на средний уровень процентной ставки и на общий дохода банка определяется просто: I_стр = I_K /I_K . В примере I_стр= I_K /I_K .= 1,1150437/1,1976047 = 0,9310615.

Для непосредственного расчета I_стр следует определить долю каждого вида кредитных услуг в базисном (d₀) и в отчетном (d₁) периодах и использовать формулу I_стр:

Виды кредита	d0	d1	S0
1. Краткосрочные	0,797006	0,702	4,7032306
2. Долгосрочные	0,202994	0,298	1,7286135

Отсюда

Таким образом, прирост валового дохода банка происходил за счет:

1) изменения объема задолженности (объема кредитных услуг)

Д(К) = Д₀ (I_ – 1) = 34,23 (1,1976047 – 1) = +6,764 млн. руб.;

2) перераспределения задолженности по разным формам кредита

Д_стр = Д₀·I_·(I_стр – 1) = 34,23∙1,1976047∙(0,9310615–1) = –2,826 млн. руб.;

3) изменения процентной ставки за кредит

Д(S) = Д₀·I_·I_стр·(I_S – 1) = 1,102 млн. руб.

Вклад разных факторов в общий прирост можно распределить по отдельным объектам совокупности , для каждого из которых применяют мультипликативную индексную модель

q₁ = q₀ · I_K ∙ i_d ∙ i_s , ∙

где q0, q1 – объемы итогового признака (дохода) по данному объекту (виду услуг);

I_K – общий для всей совокупности индекс количественного признака; is – индивидуальный для данного объекта индекс изменения уровня качественного признака;

i_d – индивидуальный индекс доли данного объекта в общем объеме количественного признака.

Распределение общего прироста валового дохода по видам кредитных услуг и по факторам в окончательном виде выглядит:

Вид кредита	Прирост валового дохода банка за счет:			Всего
	изменения объема задолженности	перераспределения задолженности по видам кредита	изменения процентной ставки
Краткосрочный	6,185	–4,468	0,883	2,60
Долгосрочный	0,579	1,642	0,219	2,44
Итого	6,764	–2,826	1,102	5,04