7.5. Множественная корреляция

Если имеется система статистических показателей: Y, X₁, X₂, …, X_m, то представляет интерес оценка корреляции между всеми парами показателей этой системы. Все парные коэффициенты корреляции могут быть представлены в одной квадратной матрице R размерностью (m+1)×(m+1), которая называется матрицей парных линейных коэффициентов корреляции. На основе матрицей R, можно определить так называемые коэффициенты множественной линейной корреляции признаков и коэффициенты парной линейной частной корреляции.

Коэффициент множественной линейной корреляции оценивает степень линейной связи одного из признаков системы с совокупностью прочих признаков этой же системы. В общем случае для измерения множественной линейной корреляции определяются параметры множественного уравнения регрессии и теоретические уровни признака-результата (например,Y). На основе фактических и рассчитанных по уравнению (теоретических) значений признака Y вычисляется коэффициент множественной корреляции R_y:

где ² – общая (фактическая) дисперсия уровней результативного признака (дисперсия Y); σ²_факт. – факторная дисперсия или дисперсия теоретических значений признака результата относительно среднего уровня; σ²_ост.– остаточная дисперсия, характеризующая вариацию Y за счет факторов, не учтенных уравнением регрессии. Известно, что общая дисперсия признака результата Y складывается из факторной и остаточной составляющих.

Коэффициент множественной корреляции изменяется от 0 до 1. Чем ближе R_Y к 1, тем более сильная связь между Y и множеством X. Если коэффициент R_Y незначителен по величине (как правило, R_Y 0,3), то можно утверждать, что или не все важнейшие факторы взаимосвязи учтены, или выбрана неподходящая форма уравнения. В последнем случае пересматривается список переменных модели и возможно, её вид.

Для нелинейной множественной связи рассчитывают индекс корреляции. Методика его вычисления аналогична, но взаимодействие факторов и функция регрессии рассматриваются как нелинейные. Индекс корреляции изменяется в пределах от 0 до 1. Квадрат R равен так называемому коэффициенту детерминации (D или R²). Он показывает, какая часть вариации зависимого признака объясняется включенными в модель факторов.

Показатели множественной корреляции рассчитываются по приведенной выше схеме не часто. Если признак-результат Y включен в общую систему признаков, то на основе общей матрицы парных линейных коэффициентов R можно получить всю совокупность коэффициентов множественной корреляции, так как любой из признаков этой системы может, в принципе, претендовать на роль признака-результата. Коэффициент множественной корреляции, оценивающий степень линейной зависимости любого признака j от всех прочих в этой системе, определяется по формуле

где (m+1) – число всех признаков в системе; |R| –определитель матрицы R парных линейных коэффициентов корреляции; R_ii – алгебраическое дополнение элемента (jj) для этой же матрицы.

7.6. Оценка статистической значимости параметров взаимосвязи

Получив оценки параметров регрессии и корреляции, необходимо убедиться, что эти значения не случайны и действительно выражают наличие, характер и тесноту зависимости признаков. Для оценки не случайности того или иного параметра или коэффициента вводится понятие уровня значимости. Уровень значимости это, в первом приближении, вероятность того, что полученное численное значение конкретного параметра (коэффициента корреляции или параметра регрессии) можно считать величиной случайной. Таким образом, чем меньше численное значение уровня значимости, тем с большей вероятностью можно утверждать, что данный параметр является неслучайным. Для экономических задач обычно достаточно, чтобы уровень значимости был численно не более 0,05 или даже 0,10. Для статистического анализа технических систем, связанных с обеспечением жизнедеятельности, уровень значимости принимается гораздо более строгим (например, не более 0,01; 0,001 или 0,0005 и т.п.).

Системы анализа статистических данных на ЭВМ обязательно включают процедуры оценки значимости. Используют любую из двух равнозначных методик. По первой, традиционной, методике исследователь задает численную оценку уровня значимости, например α = 0,05. Под эту вероятность выбирается табличное значение t-статистики Стьюдента, если оценивается значимость параметра регрессии либо коэффициента парной линейной корреляции, или табличное значение F-статистики Фишера-Снедекора для оценки значимости уравнения регрессии в целом. Далее величина конкретного полученного параметра регрессии или коэффициента корреляции пересчитывается в фактическое значение t-статистики, а для уравнения регрессии в целом в фактическое значение F-статистики. Фактические t-статистики показывают, на сколько средних квадратических отклонений соответствующий фактический параметр регрессии или корреляции отклонился от своего гипотетического нулевого среднего уровня. Для коэффициента парной линейной корреляции и параметра а₁ в уравнении парной регрессии фактическое значение t-статистики определяют Для параметра а₀:

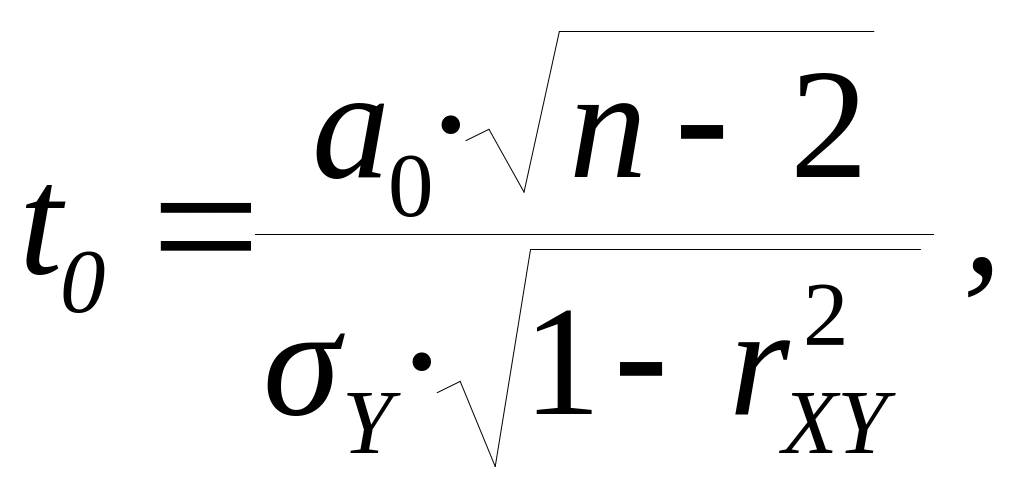
где n – количество наблюдений; r²_XY – коэффициент линейной корреляции признаков X и Y.

Для оценки значимости параметров множественной линейной регрессии: а₀, а₁, …, а_k – соответствующие значения фактических t-статистик равны

В этой формуле a_i – i-й параметр уравнения регрессии; σ_i – среднее квадратическое отклонение i-го параметра. Такая методика принята в системах статистического анализа данных на ПЭВМ.

Если фактическое значение t-статистики Стьюдента больше табличного значения (t_табл), то утверждается, что коэффициент корреляции или параметр регрессии статистически значим с уровнем, не менее α.

Согласно второй методике, определив фактическую величину t-статистики параметра регрессии, оценивают вероятность того, что за счет случайных причин эта величина могло бы быть еще большей. Если эта вероятность мала (меньше заданного численного значения уровня α), то найденный параметр признается статистически значимым. Эта методика является обычной при расчетах в системах статистического анализа данных на ПЭВМ.

При назначении табличного значения t-статистики необходимым параметром является число степеней свободы (ν). Для анализа парных линейных зависимостей число степеней свободы равно количеству наблюдений за минусом 2 (числа параметров регрессии в уравнении парной линейной связи), т.е. ν=n-2. Для уравнений множественной линейной регрессии соответственно имеем

ν = n-(k+1) = n–m,

где m – количество параметров в уравнении регрессии, n – количество наблюдений, по которым составляется уравнение множественной регрессии.

Вывод о правильности выбора вида взаимосвязи и характеристику значимости всего уравнения регрессии получают с помощью F-критерия, определяя расчетное (фактическое) значение F-статистики. На основе квадрата коэффициента множественной корреляции (R²), числа наблюдений (n) и количества параметров в уравнении множественной линейной регрессии (m) определяем

.

Полученное по этой формуле значение F_расч также должно быть больше F_теор (табличного) при v₁=m–1 и v₂=n–m степенях свободы и выбранном уровне значимости α.

(Величина F-статистики показывает, во сколько раз факторная дисперсия признака результата Y превышает его остаточную дисперсию. При расчете учитываются соответствующие степени свободы).

По второй методике определяется вероятность еще большего значения F (при тех же степенях свободы v₁=m–1 и v₂=n–m). Эта вероятность должна быть меньше принятого числа α, иначе следует пересмотреть форму уравнения, перечень переменных и т.д.