7.3. Множественная линейная регрессия

Парная корреляция и регрессия могут рассматриваться как частный случай отражения связи некоторой зависимой переменной, с одной стороны, и одной из множества независимых переменных – с другой. Когда же требуется показать связь всего множества переменных с результативным признаком Y, говорят о множественной корреляции и о множественной регрессии. На начальных стадиях обычно используют линейные модели множественной регрессии, определяя параметры соответствующих уравнений множественной линейной регрессии.

Современные вычислительные средства позволяют за короткое время получить достаточно много вариантов уравнений множественной регрессии. Анализируя варианты, можно выбрать наилучшую линейную модель и соответствующее уравнение –

Y_i.теор= а₀ + а₁ ·X_i1 + а₂·X_i2 + ... + а_k·X_ik , (i = 1, …, n),

где n – количество наблюдаемых объектов; Y_i.теор – расчетное значение регрессии, которое представляет собой оценку ожидаемого значения Y при фиксированных значениях переменных X_1, X₂, ..., X_k; а₁, а₂, ..., а_k – параметры (коэффициенты) множественной регрессии, каждый из которых показывает, на сколько единиц изменится Y с изменением соответствующего признака X на единицу при условии, что остальные признаки останутся на прежнем уровне.

Параметры уравнения множественной линейной регрессии, как правило, находятся методом наименьших квадратов, решением системы уравнений. В матричной записи эта система имеет вид

(X^T·X)·A=X^T·Y,

где

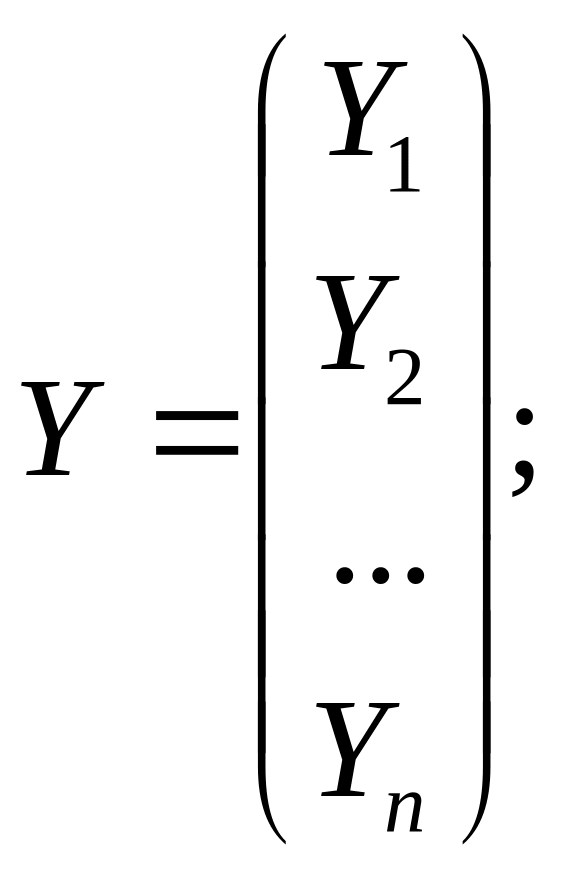
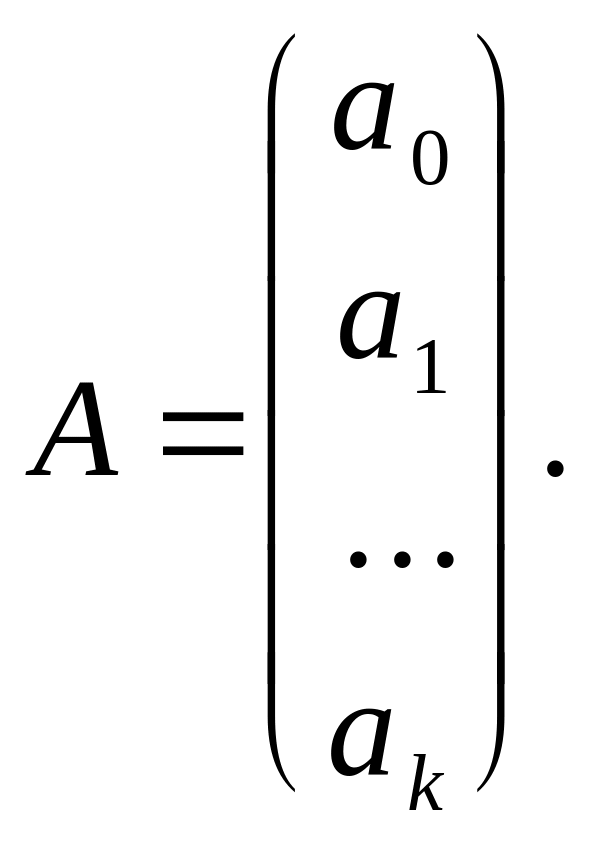
Таким образом,

.

Получение оценок параметров на ПЭВМ в настоящее время не представляет большой проблемы. Гораздо важнее, насколько та или иная форма связи соответствует реально существующей зависимости между Y, с одной стороны, и множеством X, с другой.

7.4. Нелинейная регрессия. Коэффициенты эластичности

Представление связи линейной функцией, если в действительности имеются нелинейные соотношения, приводит к ошибкам аппроксимации и упрощенным и даже ложным положениям и выводам на основе аналитического уравнения. Вопрос о линейной или нелинейной форме уравнения регрессии следует решать на стадии теоретического анализа. На практике допускается и другая методика – нелинейность формулируется как гипотеза, очерчивается круг возможных уравнений, а затем форма и вид уравнения уточняются а процессе вычислений.

Можно выделить два класса нелинейных уравнений регрессии. К первому отнесем регрессии нелинейные относительно включенных в исследование переменных, но линейные по параметрам. Это, например, полиномы различной степени. В случае парной регрессии имеем уравнения

Y= а₀ + а₁·X + а₂·X² + а₃·X³+ ... .

Множественная полиномиальная регрессия Y = f(X₁, X₂) выглядит –

Большинство используемых на практике нелинейных парных и множественных зависимостей приводятся к линейному виду заменой переменных в формуле уравнения регрессии. Так, определяя новые переменные в предыдущей формуле, как и т.д., приходим к уравнению множественной линейной регрессии:

Второй класс нелинейных функций отличается нелинейностью по оцениваемым параметрам. Наиболее известна и распространена степенная функция вида

для двух переменных либо

для множества переменных.

Коэффициенты регрессии таких нелинейных зависимостей достаточно просто определяются, если функцию удается свести к линейной форме. Например, степенную функцию можно прологарифмировать, получив линейную зависимость Y от X в логарифмах, и применить для оценки параметров уже упоминавшийся метод наименьших квадратов⁹.

Для оценки относительного влияния признака X на величину Y используют коэффициент эластичности (Э), который показывает, на сколько процентов изменится Y при изменении X на 1 процент. Расчетная формула для парной связи выглядит –

В частности, для парной степенной функции коэффициент эластичности X оказывается равным параметру регрессии а₁.

Для множественных регрессий в расчете коэффициента эластичности используется соответствующая частная производная

Для множественной степенной зависимости (мультипликативной модели) коэффициенты эластичности признаков Х равны соответствующим коэффициентам регрессии:

Эластичности признаков могут определяться для каждого конкретного наблюдения (объекта), но в настоящее время больше используются коэффициенты эластичности, когда в расчетную формулу подставляют среднее значение признака-результата и средние значения признаков факторных (признаков-регрессоров). Так, для множественной линейной регрессии эластичность признака X_i рассчитывается как