6.3. Определение численности выборки

При разработке программе выборочного наблюдения, задают величину допустимой ошибки выборки и доверительную вероятность. Неизвестным остается тот минимальный объем выборки, который должен обеспечить требуемую точность. С увеличением допустимой ошибки уменьшается необходимый объем выборки и наоборот. Например, уменьшение выборочной совокупности в 4 раза увеличивает ошибку выборки в 2 раза и, наоборот, чтобы уменьшить ошибку выборки в 2 раза, следует увеличить объем выборочной совокупности в 4 раза. Объем выборки (n) зависят от метода отбора; формулы определения минимально необходимого объема выборки приведены в табл. 6.2.

Таблица 6.2 – Минимальный объем выборки для собственно случайного и механического отбора

Метод отбора	Объем выборки
	для средней	для доли
Повторный
Бесповторный

Вариация признака (σ²) к началу выборочного наблюдения обычно неизвестна. Приближенно её задают следующими способами:

1) берут из предыдущих исследований;

2) по правилу “трех сигм” общий размах вариации укладывается в 6 сигм (H  6, отсюда   H/6). Для большей точности Н делят на 5;

3) если хотя бы приблизительно известна средняя величина изучаемого признака, то ;

4) при изучении альтернативного признака, если нет даже приблизительных сведений о доле единиц, обладающих заданным значением этого признака, берется максимально возможная дисперсия, равная 0,25.

При стратифицированном отборе, не пропорциональном объему групп, общее число отбираемых единиц делится на количество групп. Полученная величина даст объем выборки из каждой группы.

При отборе, пропорциональном числу единиц в группе, число наблюдений по каждой группе определяется формулой

где n_i – объем выборки из i-й группы; n - общий объем выборки; N_i – объем i-й группы; N – объем генеральной совокупности.

При отборе с учетом вариации признака, дающем минимальную величину ошибки выборки, процент выборки из каждой стратифицированной группы должен быть пропорционален среднему квадратическому отклонению в этой группе (_i). Расчет численности выборки (n_i) производится по формулам:

для средней для доли

При серийном (гнездовом) отборе необходимую численность отбираемых серий определяют так же, как и при собственно случайном, только вместо N, n и ² подставляют R, r и ²_м.гр., где R – число серий в генеральной совокупности; r – число отобранных серий; ²_м.гр. – межсерийная (межгрупповая) дисперсия.

6.4. Распространение выборочных результатов

Распространение выборочных оценок на генеральную совокупность состоит в определении характеристик генеральной совокупности на основе характеристик выборочной. Применяются два способа распространения выборочных данных:

1) способ прямого пересчета;

2) способ поправочных коэффициентов.

При первом способе средние величины и доли, полученные в результате исследования выборочной совокупности, переносятся на генеральную. Если известна численность генеральной совокупности, то можно оценить общий объем признака и возможные интервалы этого объема.

Например, если средняя выборочная урожайность на n=10 га зерновых культур равна 20 ц/га, а предельная ошибка урожайности (ошибка выборки) Δ =2,5 ц/га, то при известной посевной площади в N=2000 га можно установить ожидаемый объем валового сбора –

ВС = 20·2000 = 40000 ц.

Пределы возможного валового сбора оцениваются по величине дисперсии этого показателя. Допустим, что предельная ошибка выборки была оценена при доверительной вероятности равной 0,954 т.е. t=2. Тогда, используя формулу предельной ошибки выборки, заключаем, что выборочная дисперсия показателя урожайности 1 га была

.

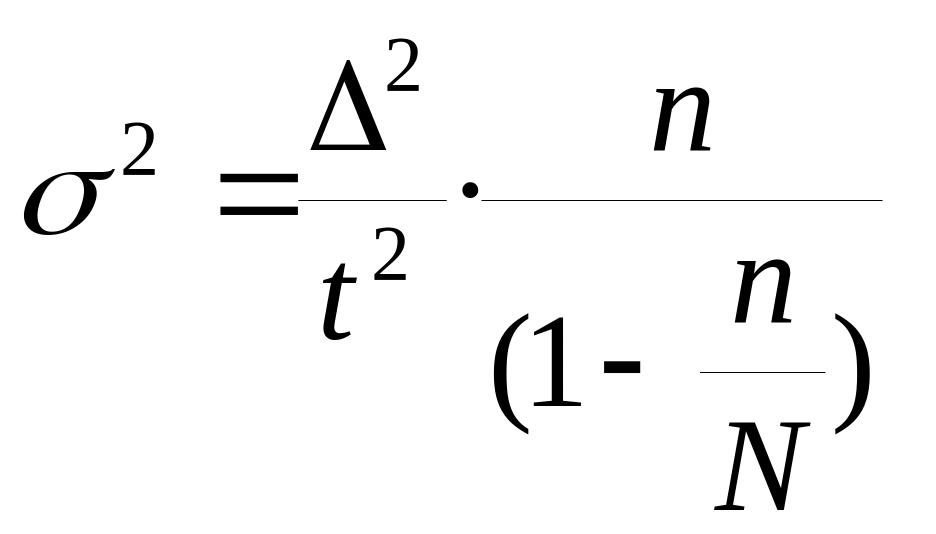Или . Таким образом, дисперсия возможного валового сбора оценивается как 15,704·2000=31407 ц².(Здесь использовано, то положение, что дисперсия суммы независимых случайных величин равна сумме дисперсий каждой случайной величины) Среднее квадратическое отклонение для всего валового сбора составляет

Следовательно, с вероятностью 0,997 (т.е. практически всегда) валовой сбор со всей площади ожидается в пределах 40000 ц. плюс-минус 3 средних квадратических отклонения, т.е. от 40000-532=39,5 тыс.ц до 40000+532=40,5 тыс. ц..

Второй способ используется для уточнения данных сплошного наблюдения. Так, если выборочное наблюдение показало, что недоучет величины исследуемого явления составил 0,5 %, то эту последнюю величину (поправочный коэффициент) распространяют на результат, полученный при сплошном наблюдении, путем увеличения его на 0,5 %.