16. Основне рівняння динаміки обертального руху.
17. Момент інерції. Теорема Штейнера. Вільні осі обертання.
Момент
інерції системи матеріальних точок
буде дорів-нюватися сумі моментів
інерції окремих точок.
Момент
інерції твердого тіла находять
інтегруванням:
.
Момент
інерції тіла є мірою інертності тіла в
обертальному русі навкруги нерухомої
осі, подібно тому, як маса тіла є мірою
його інертності при поступа-льному
русі. Таким чином можна дати наступне
визначення цей величини.
Момент
інерції –
це міра інертних властивостей твердого
тіла при обер-тальному русі, яка залежить
від розподілу маси відносно осі обертання.
Іншими словами, момент інерції залежить
від маси, форми, розмірів тіла і положення
осі обертання.
Обчислення інтеграла є достатньо складною задачею, тому наведемо формули для розрахунку моменту інерції деяких тіл правильної геометричної форми відносно осі, що проходить через центр мас . Момент інерції тіла відносно довільної осі розраховується за допомогою теореми Штейнера*. Момент інерції тіла відносно довільної осі дорівнює сумі моменту інерції відносно осі, яка проходить через центр мас паралельно даної, і добутку маси тіла на квадрат відстані між осями. Ja=Jc+md2. Слід зазначити, що будь-яке тіло, незалежно від того, обертається воно або перебуває в спокої, має момент інерції відносно будь-якої осі, подібно то-му, як тіло має масу незалежно від того, рухається воно або знаходиться у спо-кої.
18.
Момент імпульсу
тіла визначається як вектор, що дорівнює
векторному добуткові радіус-вектора
(див.
Мал. 15) положення тіла й вектора імпульсу
тіла
.
(2)
Розглянемо
момент імпульсу докладніше, прийнявши
до уваги визначення імпульсу та кутових
і лінійних характеристик обертового
руху. Н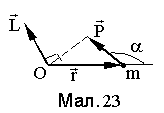
ехай
точкове тіло обертається по колу з
радіусом-вектором положення тіла
лінійній швидкості
.
Вираз (1) у цьому випадку можна послідовно
перетворити у вигляд:
(3)
,
де
,
(4)
момент
інерції тіла,
де
J
величина моменту інерції тіла.
В (3) ми використали відому формулу для подвійного векторного добутку (див. Математичний додаток)
.
Таким чином момент імпульсу (3) дорівнює
добуткові моменту інерції тіла J
на його кутову швидкість
,
які є аналогами маси тіла m
та його швидкості
у поступальному русі.
Основне
рівняння динаміки обертального руху
.
може
бути застосовано як до тіла, момент
інерції якого змінюється під час руху,
так і до системи тіл, що обертаються
навколо даної нерухомої осі. Якщо на
тверде тіло не діють зовнішні сили або
їх рівнодіюча не створює обертального
моменту відносно осі обертання, то 0=M.
У даному випадку змінення моменту
імпульсу dL=d(Jω)
дорівнює нулю. Звідси випливає закон
збереження моменту імпульсу. Якщо
на тіло не діють зовнішні сили або діють
так, що результую-чий момент цих сил
відносно осі обертання дорівнює нулю,
то момент ім-пульсу тіла відносно цієї
осі зберігається. const=Jώ
З (7.19) випливає, що кутова швидкість тіла
у цьому випадку обернено пропорційна
його моменту інерції. Закон збереження
моменту імпульсу можна записати для
системи тіл. Якщо система тіл, які
обертаються відносно деякої осі,
замкнена, то момент зо-внішніх сил
відносно цієї осі дорівнює нулю: 0=M.
В цьому випадку змінення моменту імпульсу
системи також буде дорівнювати нулю.
Це означає, що мо-мент імпульсу системи
тіл залишається незмінним. Ми отримали
закон збере-ження моменту імпульсу для
системи тіл.