55. Магнітне поле рухомого заряду сила Лоренца. Рух заряджених частинок у магнітному полі

Магнітне поле одного рухомого заряду легко розрахувати е B₀ - магнітне поле одного рухомого заряду; q_o – величина цього заряду; - середня швидкість направленого руху заряду.У векторній формі індукція магнітного поля рухомого заряду записується так

Дію магнітного поля на провідник з струмом, тобто існування сили Ампера, голландський вчений Лоренц пояснив тим, що магнітне поле діє на рухомі заряди в провіднику з струмом. Це означає, що сила Ампера є сумою сил, що діють на рухомі заряди (електрони і іони). Сила з якою магнітне поле діє на один рухомий заряд називається силою Лоренца. Позначається буквою Fл. Fл = Fа/N , N — загальна кількість зарядів в провіднику. Fл = B·I·l·sinα, I = v·noe·S Fл = B·vesinα, α – кут між B і v Напрям сили Лоренц також визначають за правилом лівої руки. Якщо ліву руку розмістити так, щоб силові лінії входили в долоню, а чотири пальці спрямовані в напрямку руху заряду якщо він позитивний і проти руху заряду якщо він негативний, тоді відведений великий палець вкаже напрям сили Лоренца . Сила Лоренца перпендикулярна до площини в якій лежать B і v і створює доцентрове прискорення, внаслідок чого заряджена частина рухається по коловій орбіті. Fл = F Fл = Bvq F = maдоц. ;aдоц. = v²/r Bvq = mv²/r => r = mv/Bq — радіус орбіти по якій рухається заряд в магнітному полі.r~v

56. Потік вектора магнітної індукції . Теорема Остроградського – Гауса для магнітного поля.

1.Потік вектора магнітної індукції

Елементарний потік dФ вектора індукції магнітного поля через елементарну поверхню dS із нормаллю (див.Мал.117) визначається скалярним добутком 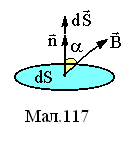, (1) де вектор . Потік через деяку незамкнену поверхню є

. (2) .2.Теорема Остроградського-Гауса для магнітного поля. Потік вектора магнітної індукції через довільну замкнену поверхню S за теоремою Остроградського-Гауса дорівнює нулю . (3) Цей результат відображає той факт, що в природі досі не знайдено магнітних зарядів (монополів Дірака), які були б джерелами магнітного поля і на яких починались чи закінчувались силові лінії. На відміну від електростатичного поля такі поля називаються соленоїдальними і вони не є потенціальними. Для доведення теореми Остроградського-Гауса (3) запишемо і, виходячи з визначення силової лінії магнітного поля ((4) §33), маємо , де dN  число силових ліній, що пронизують поверхню dS_. Тепер , (4) де N₊  силові лінії, що виходять через поверхню S, а N_  силові лінії, що входять через неї. В силу замкненості силових ліній і тому .

57.Циркуляція індукції магнітного поля.Закон повного струму

Під циркуляцією вектора розуміють інтеграл по деякому замкненому контуру L від скалярного добутку вектора та елемента дуги контуру . (1) Циркуляція індукції дорівнює (2) де сума береться по усім струмам, котрі охоплює контур L. 1. Для доведення (2), розглянемо плоский коловий контур із радіусом r, який охоплює нескінченно довгий прямий провідник із струмом І, що проходить через центр кола перпендикулярно його площині (див. Мал.112а). Вектор індукції магнітного поля , створеного струмом, направлений по дотичній до кола в кожній з його точок, а за величиною він дорівнює 3)і сталий в усіх точках кола. Скалярний добуток , бо . Тепер, підставляючи (3) у (1), одержимо (4) Таким чином вираз (1) для одного струму доведено. Розглянемо у більш загальному виді плоский довільний контур, площина якого перпендикулярна струмові І, як показано на Мал.112b. Вираз , де ми поклали, що дорівнює дузі кола радіуса r, тобто . Індукція , яку створює струм І нескінченно довгого провідника на відстані r перпендикулярна і її величина дорівнює .

Тепер циркуляцію можна записати так , що й треба було довести

2.Закон повного струму для магнітного поля в магнетику дає визначення циркуляції напруженості магнітного поля через макрострум

, (1) що проходить через поверхню S, натягнуту на замкнений контур L. Закон повного струму можна одержати, визначаючи циркуляцію , (2) де макро - та мікроструми, що проходять через поверхню S. Струм можна розрахувати, якщо допустити, що молекула з магнітним моментом еквівалентна замкнутому "виткові" молекулярного струму , (3)

58.

59. Магнітні властивості речовини Магнітне поле у магнетикові.

Розглянемо поле в середині магнетика у вигляді циліндра довжини L та радіуса основи r << L. Такий циліндр можна представити як довгий соленоїд з одним витком, по якому тече поверхневий струм І'. Cхему утворення І' із молекулярних струмів І₀' подано на Мал.47. В середині циліндра струми сусідніх молекул компенсують одне другого за рахунок їх протилежних напрямків, чого немає на поверхні циліндра. Густина витків циліндра n = 1/L, а величина індукції . По ступені й характеру намагніченості розрізняють три групи речовин: діамагнетики, парамагнетики й феромагнетики. Діамагнетиком називається речовина, яка в зовнішньому магнітному полі намагнічується і її індукція має напрямок, протилежний напрямкові індукції зовнішнього поля. До таких речовин належать Bi, Ag, Au, Cu, смоли, оргсполуки i т.п. В межах деякого об'єму намагніченість можна представити у вигляді , де N  число частинок в об'ємі , n  концентрація атомів,  магнітний момент атома. Величина є безрозмірним коефіцієнтом пропорційності, що залежить від природи середовища і визначається співвідношенням . У цьому виразі  середнє значення проекції площі орбіти на площину, перпендикулярну індукції зовнішнього поля для всіх електронів атома; Z  число електронів в атомі. Цей коефіцієнт визначає магнітну сприйнятливість . Для діамагнетиків величина i , тобто . (10)

Парамагнетиками називаються речовини, які намагнічуються в зовнішньому магнітному полі за рахунок переорієнтації власних магнітних моментів атомів Р_m із хаотичного в напрямку під дією механічного моменту сили . До парамагнетиків належать рідкоземельні елементи, Pt, Al і т.п За порядком величини, значення  для парамагнетиків практично таке ж, що і для діамагнетиків. Кюрі експериментально встановив, що величина  обернено пропорційна температурі і це співвідношення має назву закону Кюрі. Феромагнетиками називаються тверді тіла, в яких існують макроскопічні області спонтанної намагніченості - домени. До феромагнетиків належать Fe із  = 510³, суперпермалой  =810⁵ та інші. Під дією зовнішнього магнітного поля відбувається переорієнтація доменів у напрямку поля. Унаслідок досить великих значень намагніченості доменів, власне магнітне поле може бути в тисячі разів більше зовнішнього поля. При температурі Т > Т_к  температури Кюрі феромагнетик утрачає доменну структуру і має характеристики властиві парамагнетикам. Цей перехід є фазовим переходом другого роду, при якому не затрачується енергія. Наприклад, для заліза Т_К = 1043 К, для кобальту Т_К = 1403 К, для нікелю Т_К = 631 К.