- •1. Теоретические вопросы
- •2.Основные вопросы ,рассматриваемые в теоретической механике ,их краткая характеристика.
- •3.Статика. Основные определения и аксиомы статики.
- •4.Плоская система сходящихся сил. Графический и аналитический метод.
- •5. Пара сил. Равнодействующая сил. Момент пары. Условие эквивалентности пар
- •6.Плоская система произвольно расположенных сил. Уравнения статики для пространственной и плоской системы сил.
- •7. Опорные устройства балочных систем. Классификация нагрузок.
- •8.Кинематика. Кинематические характеристики простейших видов движений.
- •Простейшие движения тела.
- •9. Скорости и ускорения точек вращающегося твердого тела
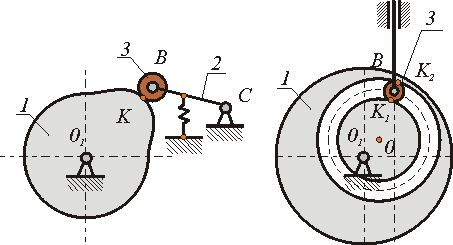
- •10. Способы передачи вращательного движения. Классификация механизмов.
- •11. Сложное движение точки.
- •12.Определение опорных реакции для балки нагруженной сосредоточенной силой.
- •13. Определение опорных реакции для балки нагруженной сосредоточенным моментом.
- •40Структура и классификация кинематических пар.
- •41Кинематические цепи и их классификация.
- •42) Механизм. Структурна формула механизма
- •43) Структурный анализ, синтез механизмов.
- •44Лишние степени свободы и пассивные связи.
- •45 Замена высших пар низшими в плоских механизмах.
- •46Структурная классификация плоских механизмов.
- •47Структурный анализ механизмов. Цель и задачи структурного анализа.
- •48Группы Ассура, их классификация.
- •50Обзор основных видов механизмов.
- •51Задачи и методы кинематического исследования механизмов.
- •52Определение положений звеньев механизма и построение траекторий точек.
- •53Определение скоростей и ускорений графо-аналитическим методом. Кривошипно-ползунный механизм.
- •54Построение плана скоростей и ускорений для шарнирного четырехзвенника.
- •Червячные передачи находят широкое применение, например, в металлорежущих станках, подъемно-транспортном оборудовании, транспортных машинах, а также в приборостроении.
12.Определение опорных реакции для балки нагруженной сосредоточенной силой.
13. Определение опорных реакции для балки нагруженной сосредоточенным моментом.
14Определение опорных реакций для балки нагруженной распределенной нагрузкой.
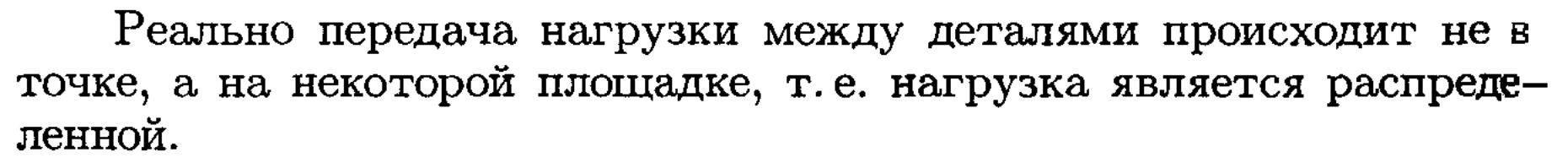
На участке балки, несущем равномерно распределенную нагрузку, поперечная сила Q изменяется по линейному закону и ее эпюра изображается наклонной прямой, а изгибающий момент изменяется по квадратичному закону и его эпюра изображается дугой параболы, выпуклость которой обращена в сторону, противоположную направлению действия нагрузки.
15 Определение опорных реакций для консольной защемленной балки нагруженной силой.
16 Динамика. Дифференциальные уравнения движения точки.
Объектом изучения динамики является:
- материальная точка
-механическая система
-абсолютно твердое тело

17Кинематические схемы зубчатых передач.
Зубчатая передача – трехзвенный механизм, в котором два подвижных звена являются зубчатыми колесами, образующими с неподвижным звеном вращательную или поступательную пару(рис.1).
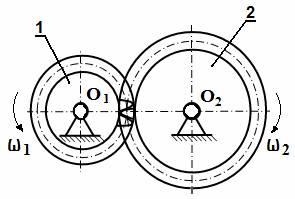
Рис.1. Зубчатая передача с внешним зацеплением
Парное зубчатое колесо - зубчатое колесо передачи, рассматриваемое по отношению к другому зубчатому колесу данной передачи. Зубчатое колесо 2 (рис.1) является парным колесу 1, зубчатое колесо 1 парное колесу 2.
Шестерня – зубчатое колесо передачи с меньшим числом зубьев.
Колесо – зубчатое колесо передачи с большим числом зубьев.
Передаточное отношение зубчатой передачи – это отношение угловой скорости ведущего зубчатого колеса к угловой скорости ведомого зубчатого колеса.
Ведущее зубчатое колесо – зубчатое колесо передачи, которое сообщает движение парному зубчатому колесу.
Ведомое зубчатое колесо - зубчатое колесо передачи, которому сообщает движение парное зубчатое колесо.
18.Кинематические схемы кулачковых механизмов.
Классификация кулачковых механизмов: Кулачковые механизмы классифицируются по следующим признакам:
по расположению звеньев в пространстве
пространственные
плоские
по движению кулачка
вращательное
поступательное
винтовое
по движению выходного звена
возвратно-поступательное ( с толкателем)
возвратно-вращательное ( с коромыслом)
по наличию ролика
с роликом
без ролика
по виду кулачка
дисковый (плоский)
цилиндрический
коноид (сложный пространственный)
по форме рабочей поверхности выходного звена
плоская
заостренная
цилиндрическая
сферическая
эвольвентная
по способу замыкания элементов высшей пары
силовое
геометрическое
При силовом замыкании удаление толкателя осуществляется воздействием контактной поверхности кулачка на толкатель (ведущее звено - кулачок, ведомое - толкатель). Движение толкателя при сближении осуществляется за счет силы упругости пружины или силы веса толкателя, при этом кулачок не является ведущим звеном. При геометрическом замыкании движение толкателя при удалении осуществляется воздействием наружной рабочей поверхности кулачка на толкатель, при сближении - воздействием внутренней рабочей поверхности кулачка на толкатель. На обеих фазах движения кулачок ведущее звено, толкатель - ведомое.
|
|
Кулачковый механизм с силовым замыканием высшей пары |
Кулачковый механизм с геометрическим замыканием высшей пары |
19Кинематические схемы шарнирно-рычажных механизмов.
- Кинематическая схема - это графическая схема отображения рабочих узлов и блоков механизма конструкции
Шарнирно-рычажные механизмы, предназначенные для передачи небольших усилий, могут иметь упрощенную конструкцию. Упрощение конструкции достигается применением скользящего соединения, при котором передача движения соприкасающимися звеньями происходит без их шарнирного соединения. Обеспечение кинематической связи между этими звеньями осуществляется силовым ( в синусном, тангенсном и поводковом механизмах) или геометрическим ( в кулисном)замыканием
Кинематический анализ шарнирно – рычажных механизмов обычно проводят на основе графических методов [1]. Считают, что они наглядны, но достаточно трудоемки и поэтому применимы для определения кинематических характеристик лишь при ограниченном количестве положений ведущего (приводного) звена. Однако основной их недостаток связан с погрешностью результатов за счет неточности измерений, отклонений от параллельности или ортогональности прямых. Погрешность возрастает при определении скоростей и, особенно, ускорений.
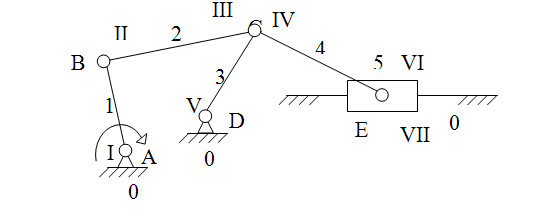
Кинематическая схема.
20Понятие передаточного числа и передаточного отношения.
Передаточное число является величиной, обратной передаточному отношению, и рассчитывается как отношение числа зубьев ведомой шестерни к числу зубьев ведущей шестерни, а также, как отношение длин окружностей в сечении (или радиусов окружностей в сечении) в точке зацепления, ведущего вала по отношению к ведомому в ремённой или фрикционной передаче. Вместо количества зубьев правильней использовать эффективные длины окружностей, или радиусы шестерней, которые определяют передачу вращающего движения, аналогично формуле для фрикционной передачи. По сути формула отношения числа зубьев является частным случаем отношения эффективных длин окружностей, вписанных в шестерни, находящиеся в зацеплении.
21Основные разделы дисциплин, изучаемых в данном курсе, их краткая характеристика.
Основные разделы дисциплины:
Классическая механика
Сопротивление материала
Теория механизмов и машин
Класси́ческая меха́ника — вид механики (раздела физики, изучающего законы изменения положений тел в пространстве со временем и причины, его вызывающие), основанный на законах Ньютона и принципе относительности Галилея. Поэтому её часто называют «ньютоновой механикой».
Классическая механика подразделяется на:
статику (которая рассматривает равновесие тел);
кинематику (которая изучает геометрическое свойство движения без рассмотрения его причин);
динамику (которая рассматривает движение тел с учётом вызывающих его причин).
Сопротивление материалов часть механики деформируемого твёрдого тела, которая рассматривает методы инженерных расчётов конструкций на прочность, жесткость и устойчивость при одновременном удовлетворении требований надежности, экономичности и долговечности. Сопротивление материалов относится к фундаментальным дисциплинамобщеинженерной подготовки специалистов с высшим техническим образованием, за исключением специальностей, не связанных с проектированием объектов, для которых прочность является важным показателем.
Теория машин и механизмов (ТММ) — это научная дисциплина об общих методах исследования, построения, кинематики и динамики механизмов и машин и о научных основах их проектирования.
22Основы сопротивления материалов. Метод сечений. Модель деформируемого тела.


Основные положения курса сопротивления материалов опираются на законы и
теоремы классической механики, в первую очередь г на законы статики твердого тела.
Механика рассматривает равновесие и движение материальных точек и абсолютно
твердых тел.
Абсолютно твердое тело — система материальных точек, расстояние между
которыми не изменяется при воздействии на твердое тело внешних усилий.
Абсолютно твердых тел в природе е существует, и использование этой модели
реального твердого тела курсе механики опирается на установленную опытом
относительную неизменность формы и размеров реальных твердых тел в определенных
условиях. Это означает, что если при воздействии внешних усилий твердое тело
подвергается незначительной деформации по сравнению с его абсолютными размерами,
то задачи, которые ставит перед собой механика, могут быть решены с высокой
степенью точности без учета этих деформаций.
Постановка же вопроса о расчете на прочность, жесткость и устойчивость абсолютно
твердого тела лишена смысла, так как оно не может ни деформироваться, ни
разрушаться.
По этой причине в курсе сопротивления материалов основной расчетной моделью
реального твердого тела является модель деформируемого твердого тела — твердого
тела, форма и размеры которого изменяются при внешнем силовом воздействии.
23.Классификация сил, действующих на элементы конструкций. Примеры.
Классификацию сил можно произвести по нескольким признакам.
Мы различаем силы сосредоточенные и распределенные.
Сосредоточенными силами называются давления, передающиеся на элемент
конструкции через площадку, размеры которой очень малы по сравнению с размерами
всего элемента, например давление колес подвижного состава на рельсы.
При расчетах, благодаря малости площадки, передающей давление, обычно считают
сосредоточенную силу приложенной в точке. Надо помнить, что это — приближенное
представление, вводимое лишь для упрощения расчета; через точку никакого давления
фактически передать нельзя. Однако неточность, вызываемая таким приближенным
представлением, настолько мала, что еe обычно на практике можно пренебречь.
Распределенными нагрузками называются силы, приложенные непрерывно на
протяжении некоторой длины или площади конструкции. Слой песка одинаковой
толщины, насыпанный на тротуар моста, представляет собой нагрузку, равномерно
распределенную по некоторой площади; при неодинаковой толщине слоя мы получим
неравномерно распределенную сплошную нагрузку. Собственный вес балки какого-либо
перекрытия представляет собой нагрузку, распределенную по длине элемента.
Сосредоточенные нагрузки измеряются в единицах силы (тоннах, килограммах,
ньютонах); распределенные по площади нагрузки выражаются в единицах силы,
отнесенных к единице площади (Т/м2
, кГ/см2
, н/м2
и т. п.); распределенные по длине
элемента—в единицах силы, отнесенных к единице длины (кГ/м, н/м и т. п.).
Далее нагрузки можно разделить на постоянные и временные. Первые действуют во
все время существования конструкции, например, собственный вес сооружения.
Временные нагрузки действуют на конструкцию лишь в течение некоторого промежутка
времени. Примером может служить вес поезда, идущего по мосту.
По характеру действия нагрузки можно разделить на статические и динамические.
Статические нагружают конструкцию постепенно; будучи приложены к
сооружению, они не меняются или меняются незначительно; таково большинство
нагрузок в гражданских и гидротехнических сооружениях. При передаче статических
нагрузок на конструкцию все ее части находятся в равновесии; ускорения элементов
конструкции отсутствуют или настолько малы, что ими можно пренебречь.
Если же эти ускорения значительны и изменение скорости элементов машины или
другой конструкции происходит за сравнительно небольшой период времени, то мы
имеем дело с приложением динамических нагрузок.
Примерами таких 'нагрузок могут служить внезапно приложенные нагрузки, ударные
и повторно-переменные.
Внезапно приложенные нагрузки передаются на сооружение сразу полной своей
величиной. Таковы давления колес локомотива, входящего на мост.
Ударные нагрузки возникают при быстром изменении скорости соприкасающихся
элементов конструкции, например, при ударе бабы копра о сваю при ее забивке.
Повторно-переменные нагрузки действуют на элементы конструкции, повторяясь
значительное число раз: Таковы, например, повторные давления пара, попеременно
растягивающие и сжимающие шток поршня и шатун паровой машины. Во многих
случаях нагрузка представляет собой комбинацию нескольких видов динамических
воздействий.
В дальнейшем мы в первую очередь займемся вопросом о сопротивлении материалов
статическому действию сил, когда вопрос о подборе сечения и материала для каждой
части конструкции решается наиболее просто.
Существуют некоторые случаи действия динамических нагрузок, которые на практике
встречаются не менее часто, чем статические, и требуют особого изучения, так как и 3
результаты воздействия таких нагрузок на элемент конструкции оказываются иными,
чем статических, и материал иначе сопротивляется этим воздействиям.
Заканчивая классификацию сил, действующих на элемент конструкции, можно
выделить воздействие тех ее частей, на которые этот элемент опирается; эти силы
называются реакциями; в начале расчета они оказываются неизвестными и
определяются из условия, что каждая часть конструкции находится в равновесии под
действием всех приложенных к ней сил и реакций.
24.Понятие о деформациях и напряжениях. План решения основной задачи сопротивления материалов
Виды напряжений. Самое важное понятие в сопротивлении материалов - это понятие напряжения как силы, действующей на малую площадку и отнесенной к площади этой площадки. Напряжения бывают трех видов: растяжения, сжатия и сдвига. Если на металлическом стержне подвешен груз,то такой стержень называется растянутым или работающим на растяжение. Напряжение S, создаваемое силой P в растянутом стержне с площадью поперечного сечения, равной A, дается выражением S = P/A. Напряжения растяжения и сжатия направлены по нормали (т.е. вдоль перпендикуляра) к площадке, в которой они действуют, а напряжение сдвига - параллельно площадке. Поэтому напряжения растяжения и сжатия называются нормальными, а напряжения сдвига - касательными.
Деформация. Деформацией называется изменение размера тела под действием приложенных к нему нагрузок. Деформация, отнесенная к полному размеру, называется относительной. Если изменение каждого малого элемента длины тела одинаково, то относительная деформация называется равномерной. Относительную деформацию часто обозначают символом d, а полную - символом D. Если относительная деформация постоянна по всей длине L, то d = D/L.
25.Типы деформаций их характеристика. Примеры.
Основными типами деформаций являются (рис. 2):
1) Растяжение или сжатие (а и б); примеры—работа цепей, канатов, тросов, растянутых и сжатых стержней в фермах, колонн;
2) перерезывание (в) — работа болтов, заклепок;
3) кручение — работа валов (г);
4) изгиб — работа всякого рода балок (д).
Эти четыре типа деформаций называются простыми.
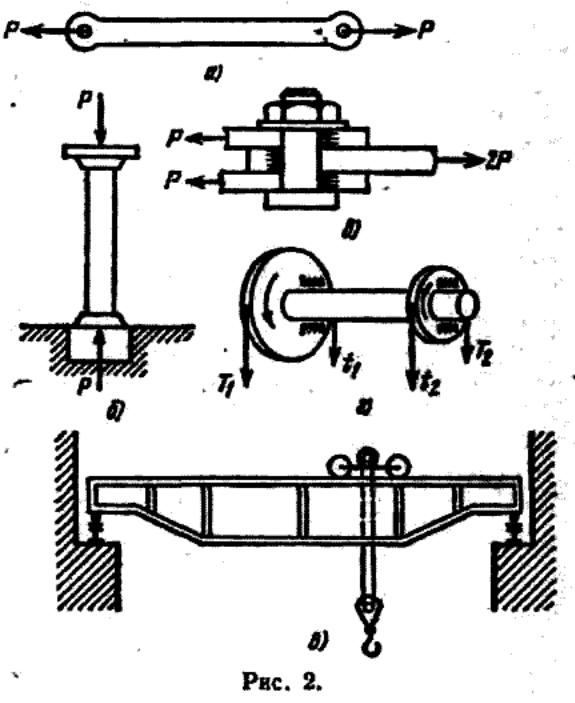
В конструкциях встречается и более сложная работа элементов, когда они испытывают два и более типов деформаций одновременно, например, растяжение или сжатие с изгибом, изгиб с кручением и т. д.; в этих случаях мы имеем дело с так называемой сложной деформацией. Для каждого из этих видов деформаций мы установим способы для вычисления напряжений, подбора материала и поперечных размеров элементов конструкции, а также способы для вычисления деформаций.
Для простоты мы будем сначала рассматривать лишь те элементы сооружений и машин, которые представляют собой так называемые призматические стержни с прямой осью. Таким стержнем мы будем называть тело, все поперечные сечения которого одинаковы; центры тяжести этих сечений лежат на одной прямой, называемой осью стержня. В дальнейшем мы рассмотрим стержни и с переменным сечением и с криволинейной осью.
26. Растяжение – сжатие, вычисление напряжений по площадкам перпендикулярным к оси стержня.
1. Вычисление напряжений по площадкам, перпендикулярным к оси стержня
Решение основной задачи сопротивления материалов мы начнем с простейшего случая
растяжения или сжатия призматического стержня.
Центральным растяжением или сжатием этого стержня называется деформация его
под действием двух равных и прямо противоположных сил, приложенных к концевым
сечениям и направленных по оси стержня. Если эти силы направлены наружу от
концевых сечений, то мы имеем растяжение (рис. 3, а), в противном случае — сжатие
(рис. 3, б).

По общему плану решения всякой задачи сопротивления материалов мы прежде всего должны найти величину этих внешних сил Р, растягивающих (сжимающих) стержень. Величина сил Р обычно может быть определена из условий взаимодействия рассматриваемого стержня с остальными частями конструкции.
В качестве простейшего примера рассмотрим стальную стяжку круглого поперечного сечения, имеющую на концах винтовую нарезку, нагруженную растягивающими

силами Р=25 Т, действующими вдоль ее оси (рис. 4). Нашей задачей будет подобрать поперечные размеры стяжки таким образом, чтобы ее прочность была обеспечена. Необходимо найти вызванные силами Р напряжения, установить для них допускаемую величину и выбрать так размеры поперечного сечения стержня, чтобы действительные напряжения не превосходили допускаемых.
Для вычисления напряжений необходимо выбрать те разрезы, которыми мы будем разделять стержень на две части. Для проверки прочности следует отыскать опасное сечение, т.е. то, через которое передается наибольшее напряжение. Мы установим формулы для вычисления напряжений сначала по сечениям, перпендикулярным к оси стержня, а в дальнейшем и по наклонным сечениям; таким путем мы сумеем отыскать наиболее опасное сечение.
Возьмем растянутый стержень и разделим его на две части поперечным сечением тп (рис. 5), перпендикулярным к оси стержня. Отбросим вторую часть; тогда, чтобы равновесие первой не было нарушено, мы должны заменить действие отброшенной части силами, передающимися на оставшуюся часть через сечение тп (рис. 6). Заменяющие силы будут уравновешивать внешнюю силу Р, поэтому они должны сложиться в равнодействующую N, равную Р, направленную по оси стержня в сторону, противоположную внешней силе (рис. 6). Эта равнодействующая N будет усилием, действующим в стержне.
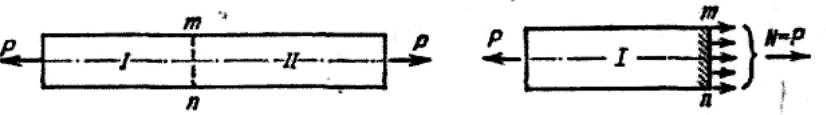
В дальнейшем мы будем называть нормальным или продольным усилием равнодействующую внутренних сил упругости, передающихся через мысленный разрез от одной части стержня к другой. Но так как отрезанная часть стержня должна находиться в равновесии под воздействием продольного усилия и внешних сил, приложенных к рассматриваемой части, то это усилие может быть вычислено и через внешние силы. Оно численно будет равно равнодействующей внешних сил, приложенных к рассматриваемой части стержня, и направлено в сторону, противоположную этой равнодействующей. Если усилие направлено внутрь 19 рассматриваемой части, то стержень сжат, если в противоположную сторону, то растянут.
Следовательно, условия равновесия оставшейся части дают нам лишь величину равнодействующей внутренних сил, передающихся по сечению тп, ее направление и точку приложения, но не могут указать, как распределяются напряжения по сечению, т. е. какие силы будут передаваться через различные части этого сечения. Между тем для оценки опасности, угрожающей прочности материала, необходимо найти наибольшее напряжение, отыскать ту часть сечения, через которую передается наибольшая сила.
Опыты с растяжением стержней из различных материалов показывают, что если растягивающие силы достаточно точно совпадают с осью стержня, то удлинения прямых линий, проведенных на поверхности стержня параллельно его оси, будут одинаковы. Отсюда возникает предположение о равномерном распределении напряжений по сечению. Лишь у концов стержня, там, где происходит непосредственная передача сил Р на стержень, растяжение распределяется неравномерно между отдельными участками сечения: те участки,, к которым непосредственно приложена сила Р, перегружаются, но уже на небольшом расстоянии от концов работа материала выравнивается, и наступает равномерное распределение напряжений по сечению, перпендикулярному к оси. Эти напряжения направлены параллельно силе Р, т. е. нормально к сечению; поэтому их называют нормальными напряжениями и обозначают буквой ζ. Так как они распределены равномерно по сечению, то N= ζ·F; с другой стороны, N=P; отсюда получаем
![]()
Эта формула позволяет нам вычислить напряжение ζ, если известны растягивающая сила и размеры сечения стержня. С другой стороны, если мы зададимся допустимой величиной нормального напряжения, из этой же формулы можно будет найти необходимую площадь поперечного сечения F.
27Деформации при растяжении – сжатии. Закон Гука.
Опыты приводят к заключению, что пока нагрузка на образце не достигла известного предела, удлинение прямо пропорционально растягивающей силе Р, длине образца l и обратно пропорционально площади поперечного сечения F. Обозначая через Δl приращение длины образца от силы Р, можем написать формулу, связывающую Между собой эти опытные данные:

где Е —коэффициент пропорциональности, различный для разных материалов. Величина Δl называется абсолютным удлинением стержня от силы Р. Формула (2.5) носит название, закона Гука, по имени ученого, впервые открывшего этот закон пропорциональности в 1660 г.
Зависимость (2.5) можно представить в ином виде. Разделим обе части этой формулы на первоначальную длину стержня
![]()
отношение Δl/ l — абсолютного удлинения к первоначальной длине — называется относительным удлинением; оно обозначается буквой ε.
Относительное удлинение является безразмерной величиной, как отношение двух длин Δl и l, и по своему числовому значению равно удлинению каждой единицы длины стержня. Подставив в предыдущую формулу вместо Δl/ l величину ε, а вместо P/F — величину нормального напряжения ζ, получаем иное выражение закона Гука:
![]()
![]()
Таким образом, нормальное напряжение при растяжении или сжатий прямо пропорционально относительному удлинению или укорочению стержня.
Коэффициент пропорциональности Е, связывающий нормальное напряжение и относительное удлинение, называется модулем упруготи при растяжении (сжатии) материала. Чем больше эта величина, гм менее растягивается (сжимается) стержень при прочих равных условиях (длине, площади, силе Р). Таким образом, физически модуль Е характеризует сопротивляемость материала упругой деформации при растяжении (сжатии).
Так как ε— относительное удлинение— является безразмерной величиной, то из формулы (2.7) следует, что модуль выражается в тех же единицах, что и напряжение ζ, т. е. в единицах силы, деленных на единицу площади. , Надо заметить, что величина модуля упругости материала Е даже для одного и того же материала не является постоянной, а несколько колеблется. Для некоторых материалов величина модуля оказывается одинаковой как при растяжении, так и при сжатии (сталь, медь), в других случаях— различной для каждой из этих деформаций. В обычных расчетах этой разницей пренебрегают и принимают для громадного большинства материалов одно и то же значение Е как при растяжении, так и при сжатии.
Надо иметь в виду, что закон Гука представлен формулой, которая только приближенно отражает результаты опытов, схематизируя их; поэтому он не представляет собой совершенно точной зависимости.
Все материалы при растяжении или сжатии дают величины деформации, более или менее отклоняющиеся от этого закона. Для некоторых материалов (большинство металлов) эти отклонения ничтожны малы, и можно считать, что осуществляется полная
пропорциональность между деформацией и нагрузкой; для других (чугун, камень, бетон) — отклонения значительно больше.
Однако для практических целей мы можем пренебречь наблюдающимися небольшими отклонениями от формул (2.5) и (2.6) и пользоваться ими при вычислении деформаций стержней.
Средние величины модуля Е для ряда материалов даны в таблице 1.
Из рассмотрения формулы (2.5) ясно, что чем больше ее знаменатель, тем менее растяжим (податлив) или, как говорят, тем более жесток стержень, поэтому знаменатель формулы (2.5) , величина EF, начинается жестокостью стержня при растяжении или сжатии. Мы видим, что жесткость при растяжении или сжатии зависит, с одной стороны, от материала стержня, характеризуемого величиной его модуля упругости Е, а с другой стороны, от размеров поперечного сечения стержня характеризуемых величиной площади его поперечного сечения F. Иногда бывает удобно пользоваться понятием жесткости, которая равна EF/1, т. е. отношению жесткости стержня к длине.
Формули (2.5) и (2.6) позволяют определить удлинения и укорочения которые получает тот или иной стержень конструкции при растяжении или сжатии. Обратно, зная эти удлинения, размеры и материал стержня, можно вычислить нормальные напряжения, которые в нем возникают. Таким образом, для вычисления напряжений ζ мы имеем два пути: если известны внешние силы Р, растягивающие или сжимающие стержень, то σ вычисляется по формуле (2.1)
![]()
если же внешние силы неизвестны, а можно измерить удлинение стержня, то в определяется формулой (2.7)
![]()
Величина относительного удлинения может быть вычислена, если мы измерим абсолютное удлинение Δl участка стержня длиной l и применим формулу
![]()
28.Диаграммы растяжения. Механические характеристики материалов.
С точки зрения различия в механических качествах при простом растяжении и сжатии и при обычной температуре материалы могут быть хрупкими или пластичными. Хрупкие материалы разрушаются при очень малых остаточных деформациях. У пластичных же материалов разрушение наступает лишь после значительной остаточной деформации. К первому типу материалов относятся, например, чугун, камень, бетон и др. К пластичным материалам относятся малоуглеродистая сталь, медь и др. Выясним сначала поведение обоих типов материалов в опыте на растяжение вплоть до разрушения. Для этого опыта изготовляется образец призматической формы круглого или прямоугольного сечения. На рабочей части образца наносят деления через каждый сантиметр или доли сантиметра, чтобы иметь возможность после опыта судить об изменении длины образца. Образец помещают в машину и закрепляют его концы. Медленно перемещая один конец образца в направлении его оси, стержень растягивают нагрузкой, которая возрастает постепенно, без толчков и ударов. При опыте отмечают ряд последовательных величин нагрузки и измеряют соответствующее им увеличение длины l, намеченной на образце. Результаты измерений нагляднее всего можно представить в виде так называемой диаграммы растяжения; на большинстве машин имеется приспособление, автоматически вычерчивающее эту диаграмму при растяжении образца. При вычерчивании диаграммы по вертикальной оси откладываются в определенном масштабе нагрузки, а по горизонтальной — абсолютные удлинения. При растяжении образца из пластичного материала (например, малоуглеродистой стали) диаграмма имеет вид, показанный на рис.12. Первая часть диаграммы до точки А, соответствующей пределу пропорциональности, представляет собой прямую линию. Ордината ОА1 представляет собой величину растягивающей силы, соответствующей пределу пропорциональности ζв , т.е. тому наибольшому напряжению, превышение которого вызывает отклонение от закона Гука; для малоуглеродистой стали величина ζп равна примерно 2000 кГ/смг. Это напряжение определяется по формуле (2.1),
![]()
где в качестве площади поперечного сечения F принимается ее первоначальная величина. Такое напряжение называется условным. В дальнейшем использование первоначальной площади поперечного сечения обычно не будет особо оговариваться. Определение «условное» также обычно опускается.
При увеличении растягивающей силы за величину OA1 деформация начинает расти быстрее нагрузки — диаграмма имеет криволинейный вид с выпуклостью вверх. Далее наблюдается резкое изменение в работе материала; при некотором значении растягивающей силы ОС1 материал «течет»; для увеличения деформации почти не нужно увеличивать растягивающую силу.
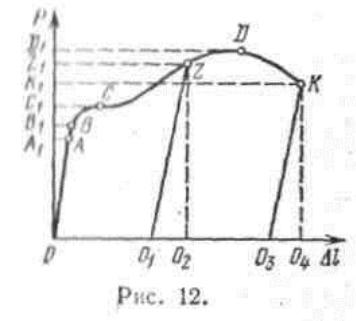
На диаграмме образуется горизонтальная (или почти горизонтальная) площадка.
Напряжение, при котором происходит такое течение материала — рост деформаций при постоянной (примерно) нагрузке, называется пределом текучести ζт. Для малоуглеродистой стали ζт ≈2400 кГ/см2.
29Статически неопределимые системы. Силовой фактор.
Системы, в которых количество наложенных связей больше, нежели число независимых уравнений равновесия, называются статически неопределимыми.
N-продольная сила(растяжение-сжатие)
Qx Qy –поперечная сила(сдвиг)
Mk –крутящий момент
Mx,My-изгибающий момент
30Статически неопределимые системы. Системы, в которых количество наложенных связей больше, нежели число независимых уравнений равновесия, называются статически неопределимыми.
Монтажный фактор.
31.Статически неопределимые системы. Системы, в которых количество наложенных связей больше, нежели число независимых уравнений равновесия, называются статически неопределимыми.
Температурный фактор.
32.Основные гипотезы и допущения в сопротивлении материалов.

Гипотеза о сплошном строении тела, Гипотеза об идеальной упругости тела. Гипотеза об однородности, Гипотеза об изотропности материала, Гипотеза плоских сечений.
33.Гипотеза о сплошном строении тела. Материал считается:сплошным, если в теле нет разрывов;
Гипотеза об идеальной упругости тела. - (упругость - способность тел восстанавливать свою форму и размеры при выгрузке) Гипотеза об однородности. Гипотеза сплошного однородного тела. Она состоит в том, что реальное тело, состоящее из атомов и молекул, заменяется гипотетическим сплошным однородным телом. Тело или среда называется сплошной, если любой выделенный малый объем содержит вещество. Однородность означает, что свойства тела во всех точках одинаковы. Наиболее распространенные в технике материалы – неоднородны, они имеют зачастую (напр. металлы) кристалическое строение и свойства элементов по разному выделенных из кристаллов различны.
34.Гипотеза об изотропности материала. Материал считается: изотропным, если его свойства во всех направлениях одинаковы. Отдельно взятый кристалл материала анизотропен, но так как в объеме реального тела содержится бесконечно большое количество хаотично расположенных кристаллов, принимается, что материал изотропен1
Гипотеза
плоских сечений.

Допущение о малости деформаций. Гипотеза (допущение) о малости деформаций: деформации в точках тела считаются настолько малыми, что не оказывают существенного влияния на взаимное расположение нагрузок, приложенных к телу.
35Деформация изгиба.
Деформация изгиба — вид деформации, при котором нарушается прямолинейность главной оси тела. Деформации изгиба испытывают все тела подвешенные на одной или нескольких опорах. Каждый материал способен воспринимать определенный уровень нагрузки, твердые тела в большинстве случаев способны выдерживать не только свой вес, но и заданную нагрузку. В зависимости от способа приложения нагрузки при изгибе различают чистый и косой изгиб.
Правило
знаков при построении эпюр.

Контроль правильности построения эпюр. 1.если брус загружен сосредоточенными силами и моментами то Q=const, М-линейна 2.если брус загружен равномерно распределенной нагрузкой, то эпюры Q-линейна, М-параллельна.3.Если на каком-то участке Q=0, то М=const 9чистый изгиб).4.в той точке где Q=0,то М-экстремален 5.В сечениях приложенных сосредоточенных сил на эпюре Q происходит скачок на величину приложенной силе,а на эпюре М возникает излом. 6.Скачок на эпюре моментов м.б. только в сечении, где приложен сосредоточенный момент. Величина скачка равна приложенному моменту.
Условие прочности.
36Практический расчет на изгиб валов.
37Основные понятия и определения в теории механизмов и машин.
Теория механизмов и машин-это наука изучающая строение и кинематику, динамику, в связи с их анализом и сентезом.
Анализ-исследование структурных кинемат-х и динами-х свойств механизма.
Синтез-это проектирование механизмов с заданными структурными кинемат.и динам-х свойств.
38.Классификация машин и механизмов.
Машина-это устройство выполняющее механические движения для преобразования энергии, материала и информации с целью замены или облегчения физического и умственного труда человека.
Бывают: Информационные машины, Рабочие машины , Энергетические машины
Механизмы- это система тел предназначенная для преобразования движения одного или нескольких тел в требуемое движение других твердых тел.Классифицируются:кулачковые,шарнирно-рычажные,зубчатые,винтовые и клинчатые, фрикционные механизмы
39.Строение механизмов. Определение звена. Звено – одна или несколько неподвижно соединенных друг с другом деталей, входящих в механизм и движущихся, как одно целое. координаты входных звеньев (линейные и угловые) определяют положение всех звеньев цепи.