8.Кинематика. Кинематические характеристики простейших видов движений.

Кинематика –изучает механическое движение без учета сил, вызывающих это движение или влияющих на него. Таким образом, устанавливаются некоторые количественные меры движения с чисто геометрической точки зрения.

Основные понятия.

1. Траектория – линия, которую очерчивает материальная точка при движении в пространстве.

Уравнение траектории: у = f(х).

2. Пройденный путь – длина траектории, [S], м.

3. Скорость движения – векторная величина, характеризующая в данный момент времени быстроту движения точки, [v], м/с.

Направлена в любой момент времени по касательной к траектории в сторону направления движения.

4. Ускорение - векторная величина, характеризующая в данный момент времени быстроту изменения скорости по величине и направлению, [a], м/с².

Раскладывается на нормальное (а_n = v²/r), и касательное (а_t = dv/dt = v^/ = S^//) : а = √а_n² + а_t².

2. Простейшие движения тела.

   1. Поступательное – движение твердого тела, при котором всякая прямая линия на теле при движении остается параллельной своему первоначальному положению.

Все точки тела движутся одинаково, поэтому рассматривается движение центра масс.

2. Вращательное – движение, при котором все точки тела описывают окружности вокруг общей неподвижной оси, называемой осью вращения.

Описывается угловыми параметрами:

• φ – угол поворота [φ] = рад.

• ω – угловая скорость, определяет изменение угла поворота в единицу времени,

ω] = рад/с. ω = dφ/dt;.

• ε – угловое ускорение, изменение угловой скорости со временем, [ε] = рад/с², ε = dω/dt.

• Частота вращения – число оборотов в минуту, [n] = об/мин.

ω = 2πn/60 = πn/30.

3. Частные случаи вращательного движения.

   1. Равномерное : ω =const, φ = φ₀ + ωt

φ = φ₀ + ωt ω =const

2. Равнопеременное:

ε = const, φ = φ₀ + ω₀ t + εt²/2, ω = ω₀ + εt.

φ = φ₀ + ω₀ t + εе²/2. ω = ω₀ + εt. ε = const

9. Скорости и ускорения точек вращающегося твердого тела

Вращением твердого тела вокруг неподвижной оси назывется такое движение тела , при котором в теле найдутся по крайней мере две точки, которые все время движения будут оставаться неподвижными. Прямая, проведенная через эти точки называется осью вращения твердого тела.

Вращательное движение твердого тела определено, если задан как функция времени угол, на который поворачивается плоскость, проходящая через ось вращения и какую-нибудь точку вращающегося тела:

где - непрерывная дважды дифференцируемая функция времени.

Алгебраическая угловая скорость вращения тела

.

Угловую скорость можно определить и как вектор, расположенный на оси вращения и равный , где - единичный вектор, задающий положительное направление оси вращения. Численное значение угловой скорости равно модулю вектора :

.

Единица измерения в СИ - рад/с.

Изменение угловой скорости тела во времени характеризуется угловым ускорением.

Алгебраическим угловым ускорением тела называется первая производная от алгебраической угловой скорости или вторая производная по времени от угла поворота вокруг неподвижной оси:

.

Как векторную величину угловое ускорение можно определить так:

.

Проекция углового ускорения на ось вращения

,

т.е. она равна алгебраическому угловому ускорению тела, если положительные направления отсчета угла и оси соответствуют правой декартовой системе координат. Значение (модуль) углового ускорения

.

Единица измерения углового ускорения в СИ - рад/с².

Векторы и являются скользящими векторами, расположеными на оси вращения тела. Вращательное движение называется ускоренным, если и замедленным, если , при тело вращается равномерно, в этом случае .

Скорость точки А определим в виде (рис.2). В данном случае , так что поскольку , то В итоге получаем

,

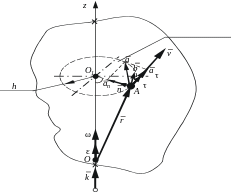
которая называется векторной формулой Эйлера.

Модуль скорости точки определятся как Скорости точек при вращении вокруг неподвижной оси направлены по касательной к окружности радиусом в соответствии с направлением угловой скорости тела.

Ускорение точки А тела Здесь

следовательно

Рис.2

Слагаемые в правой части представляют собой касательную и нормальную составляющие ускорения точки.

Молуль касательного ускорения равен

Вектор всегда направлен по нормали к траектории точки в сторону ее вогнутости (к оси вращения тела). Модуль нормального ускорения точки

Полное ускорение точки тела, вращающегося вокруг неподвижной оси,

.

Его численное значение (модуль) определяется по формуле:

Таким образом, модули скоростей и ускорений точек тела, вращающегося вокруг неподвижной оси, прямопропорциональны кратчайшему расстоянию от них до оси вращения, причем, чем дальше находится точка от оси вращения, тем больше ее скорость иускорение.

Так как траектории точек вращающегося тела – окружности, при определении скорости и ускорения удобно воспользоваться естественным способом задания движения (рисунок 1.5). Дуговая координата, определяющая положение точки на траектории, связана с углом поворота равенством:

s = φR . Отсюда:

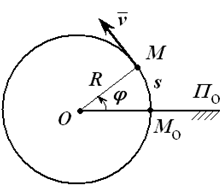
Рис. 1.5

Скорость ν = ν_ττ еще называют линейной или окружной скоростью. Она направлена по касательной к траектории движения точки.

Ускорение (рисунок 1.6) определяется как сумма касательного и нормального ускорений:

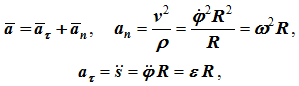
модуль ускорения

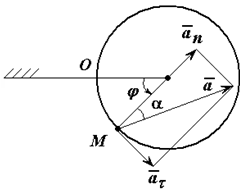
Рис. 1.6

Угол α, образованный вектором ускорения точки с радиусом окружности OM, для всех точек тела в любой момент времени одинаков,

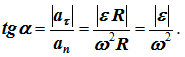
Касательное и нормальное ускорения при вращательном движении твердого тела также называют соответственно вращательным и центростремительным: