Задачі для самостійного розв'язання

1. Обчислити інтеграли.

а) ; б) ; в) ; г) .

2. Обчислити інтеграли за замкнутим контуром.

а) ; б) ; в) ; г) .

Ряди Лорана, ізольовані особливі точки

Функція , однозначна й аналітична в кільці (не виключаються випадки, коли та ), розкладається у цьому кільці в ряд Лорана

.

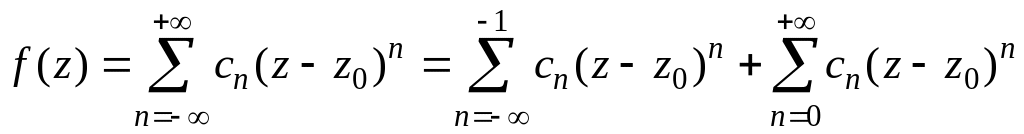У цій формулі ряд

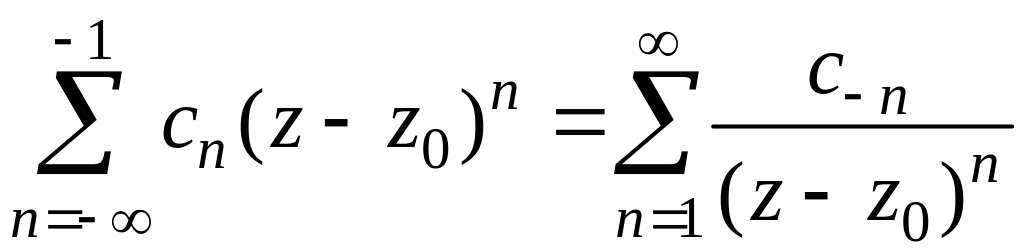
називається головною частиною ряду Лорана, а ряд

називається правильною частиною ряду Лорана.

На практиці, якщо це можливо, використовують відомі розкладання в ряд Тейлора елементарних функцій. Наприклад, такі:

,

,

,

,

,

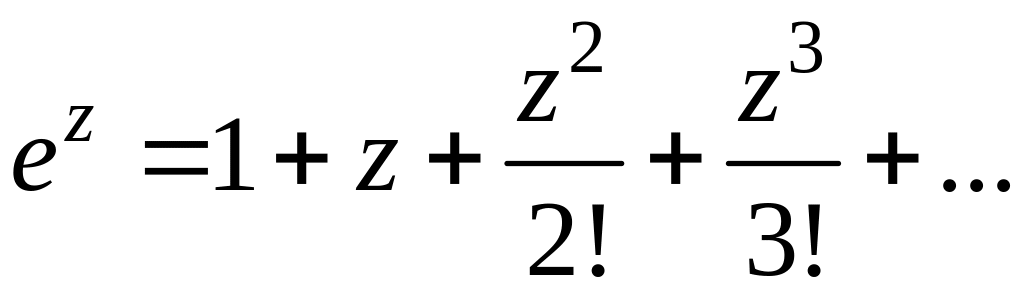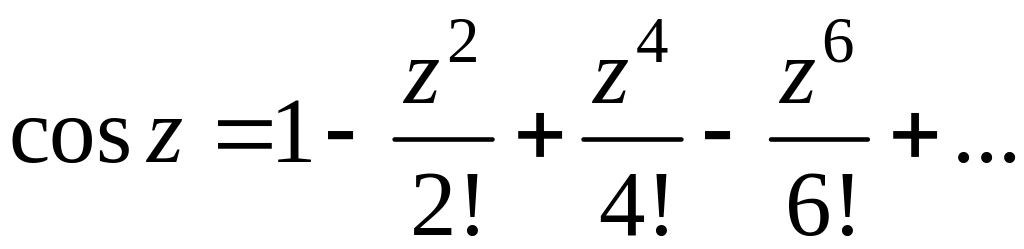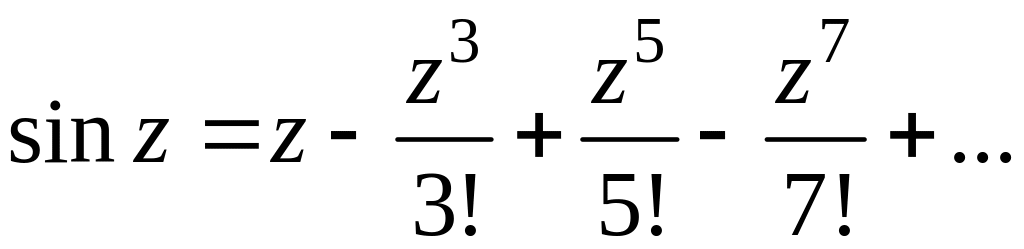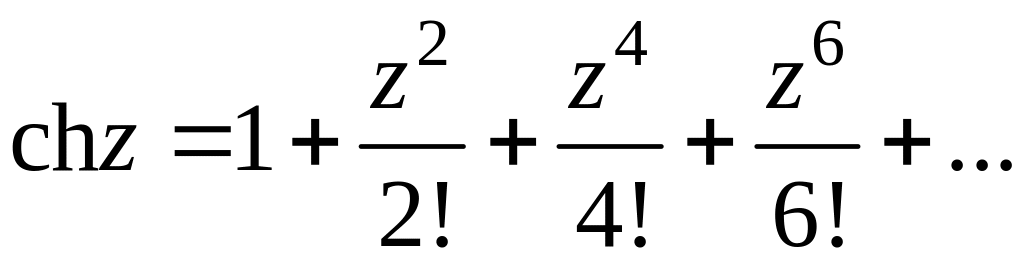(ці розкладання мають місце при )

( ).

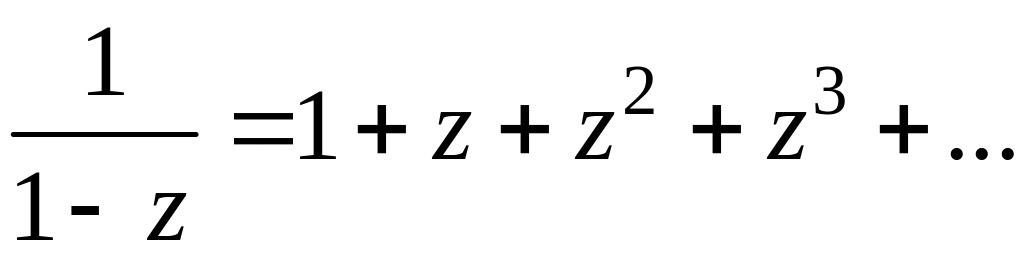Задача 7. Розкласти функцію в ряд Лорана.

а) 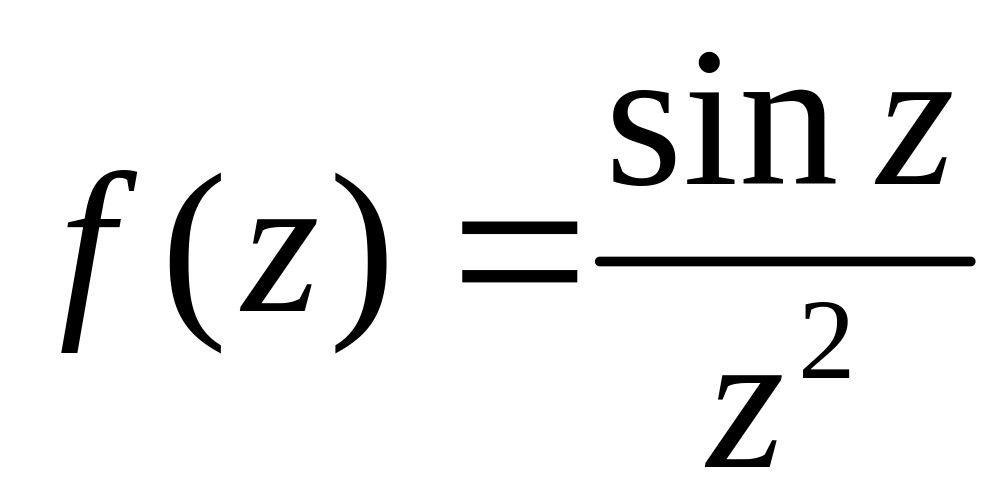у околі точки ;

б) в околі точки ;

в) у кільці .

Розв’язання. а) Скористаємось відомим розкладанням

.

Маємо

.

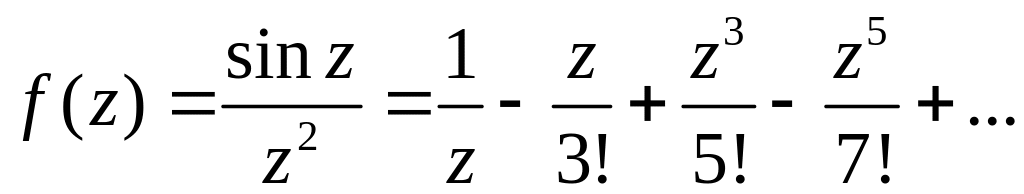б) Перетворимо задану функцію:

.

Тепер скористаємось відомим розкладанням

,

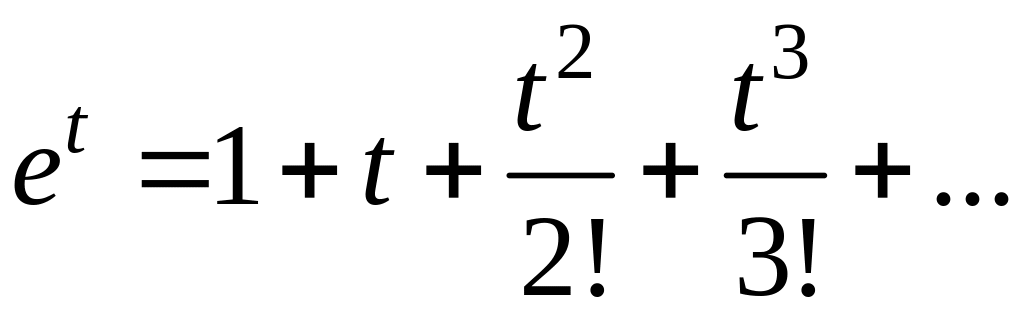поклавши в ньому 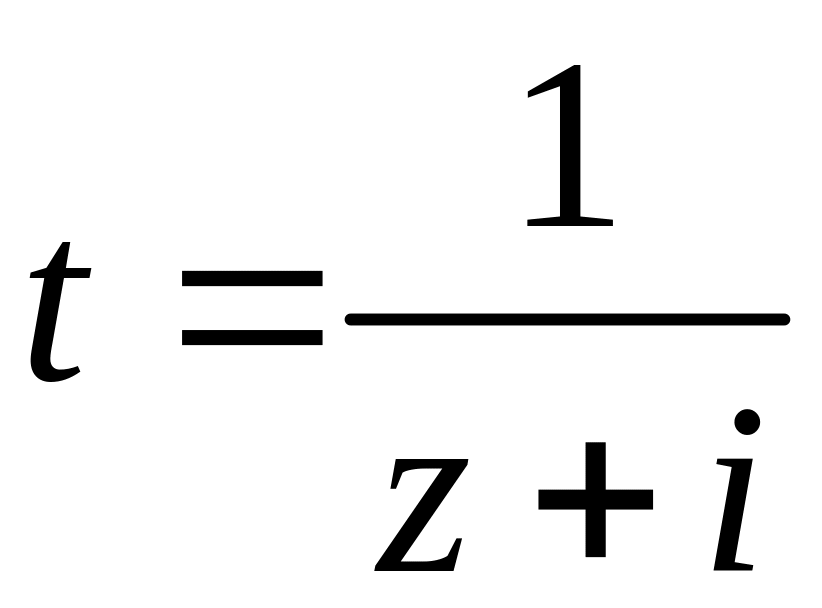. Одержимо

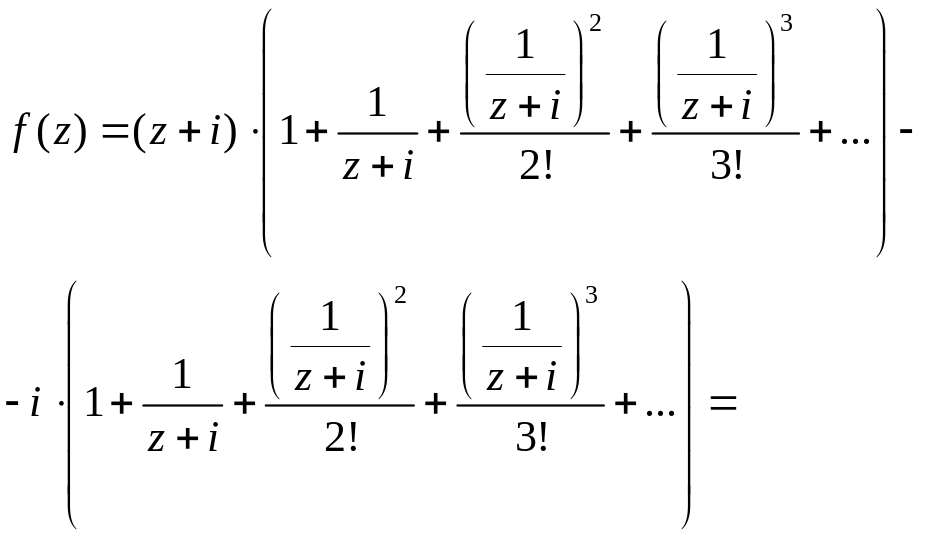
в) Розкладемо задану функцію на елементарні дроби, та виконаємо перетворення:

.

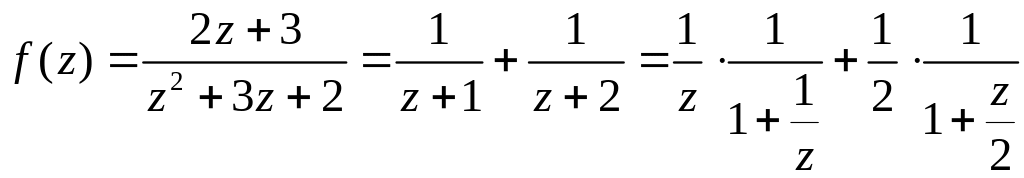Тепер, врахувавши, що у кільці 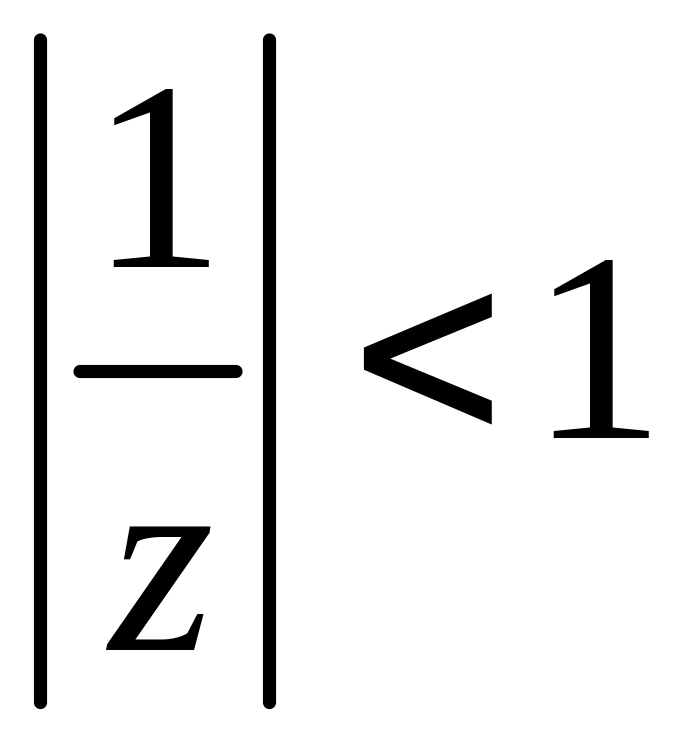, та 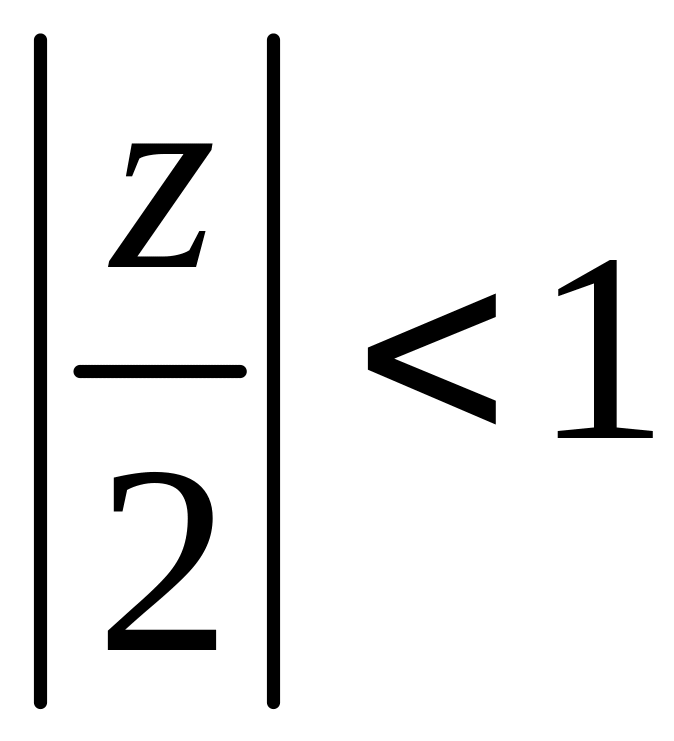, використаємо розкладання

.

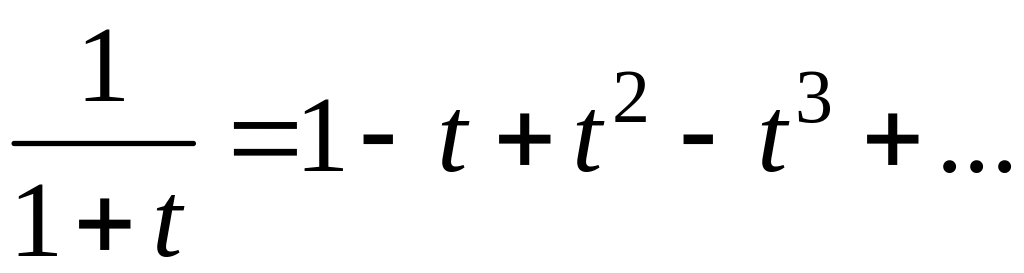Одержимо

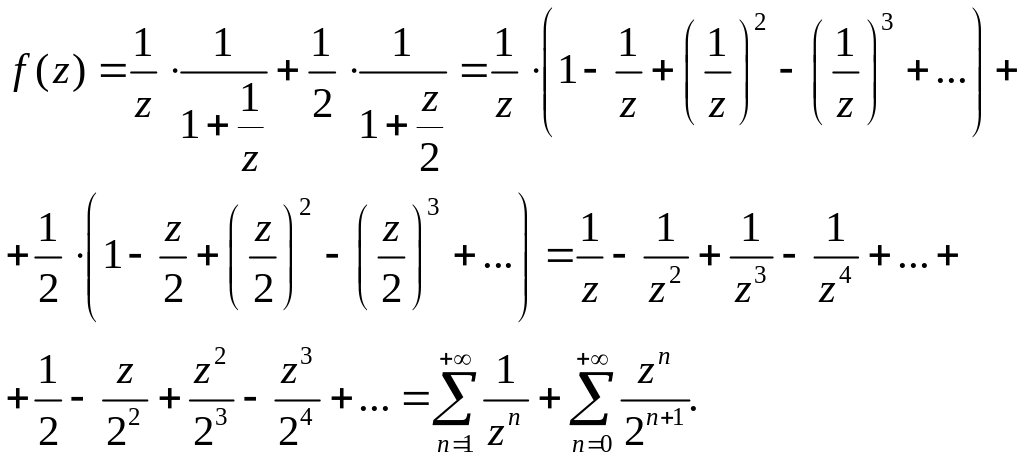
Точка називається ізольованою особливою точкою функції , якщо існує окіл цієї точки, в якому функція аналітична всюди, окрім точки .

Функцію в околі точки можна розкласти в ряд Лорана. При цьому можливі три різних випадки, коли ряд Лорана:

1) не містить членів з негативними степенями , тобто

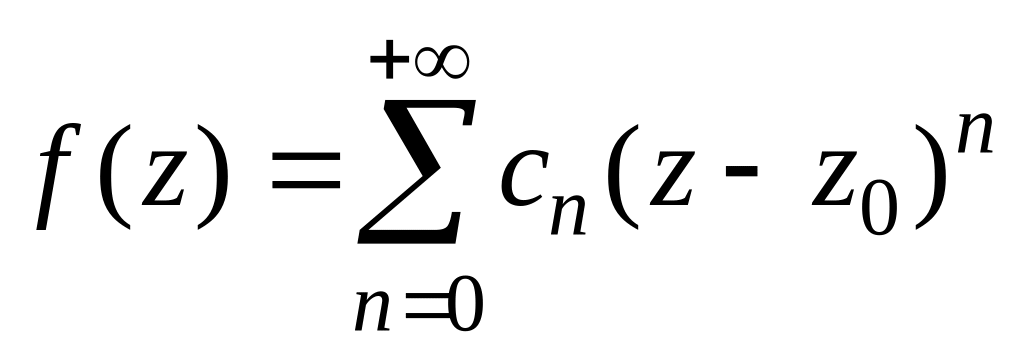
(ряд Лорана не містить головної частини). У цьому випадку називається усувною особливою точкою функції .

2) містить скінчене число членів з від'ємними степенями , тобто

,

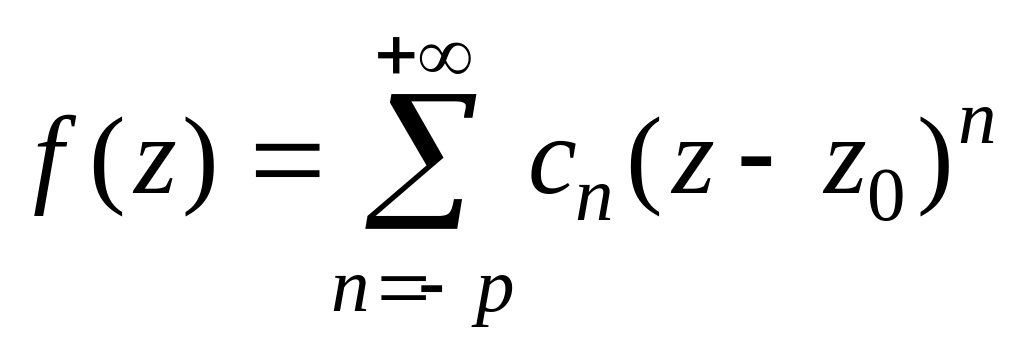причому . У цьому випадку точка називається полюсом порядку p функції .

3) містить нескінченне число членів з від'ємними степенями , тобто

.

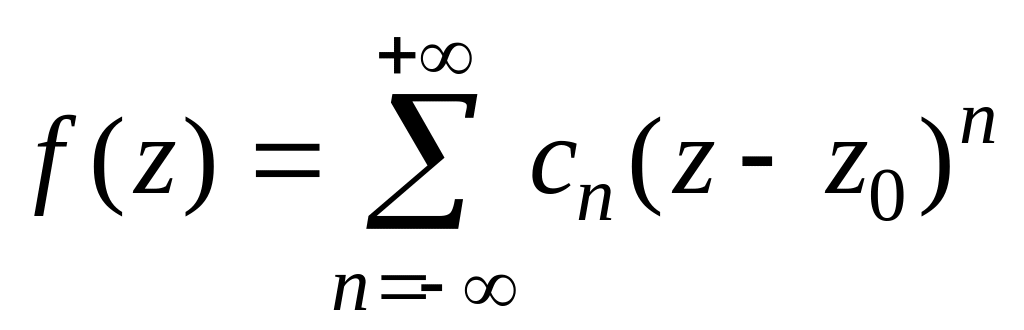У цьому випадку точка називається істотно особливою точкою функції .

При визначенні характеру ізольованої особливої точки інколи не обов'язково шукати розкладання функції в ряд Лорана. Наприклад, для того, щоб точка була полюсом порядку p, необхідно і достатньо, щоб її можна було подати у вигляді

,

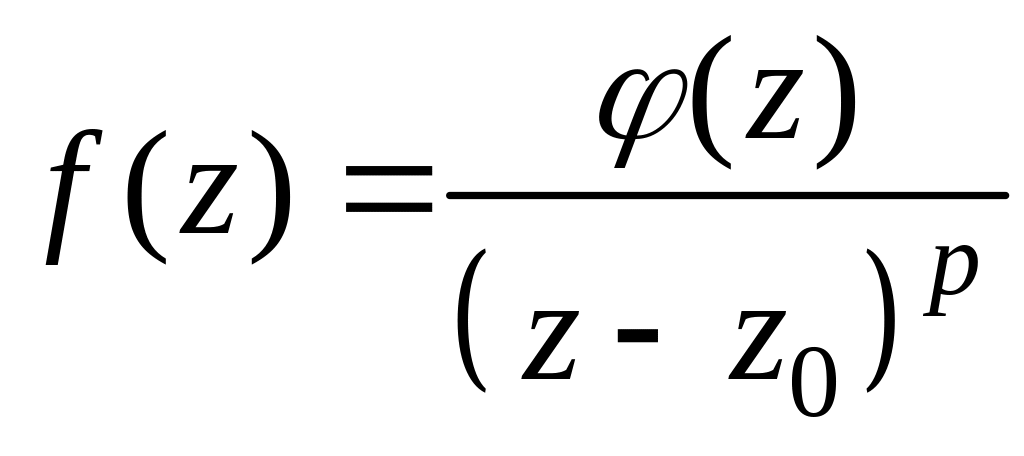де – аналітична у точці і .

Для того, щоб точка була усувною особливою точкою функції необхідно і достатньо, щоб у цій точці функція мала скінчену границю.

Задача 8. Визначити особливі точки функцій та вказати їх тип.

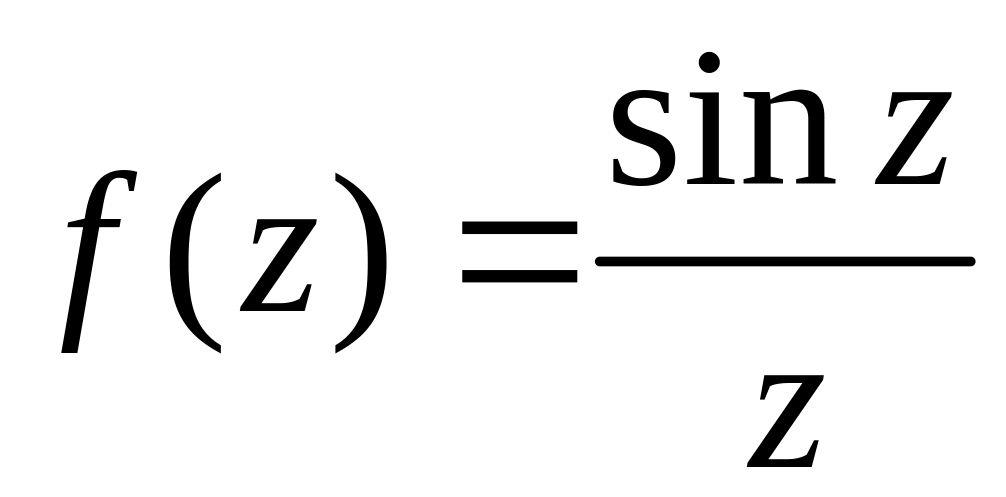а) ; б) ; в) .

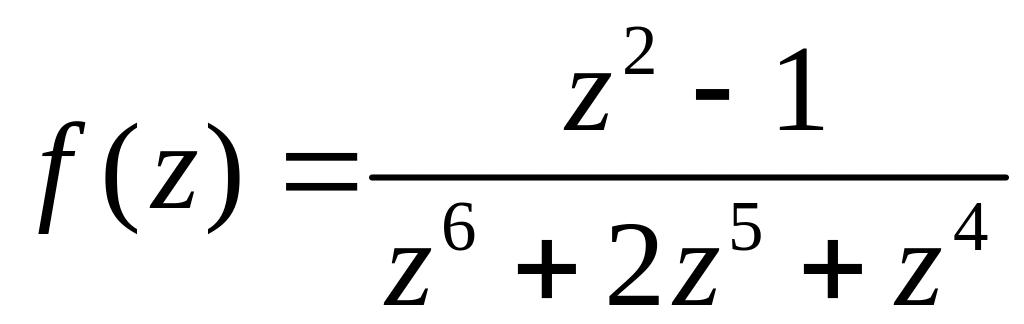Розв’язання. а) Дана функція має розрив у точці , значить ця точка є особливою. Розкладемо функцію в ряд Лорана, використовуючи відоме розкладання

.

Маємо

.

Оскільки головна частина ряду Лорана містить нескінчену кількість членів, то точка є істотно особливою точкою функції.

б) Точка не належить області визначення заданої функції, значить вона є особливою точкою. Розкладемо функцію в ряд Лорана, використовуючи відоме розкладання

.

Маємо

.

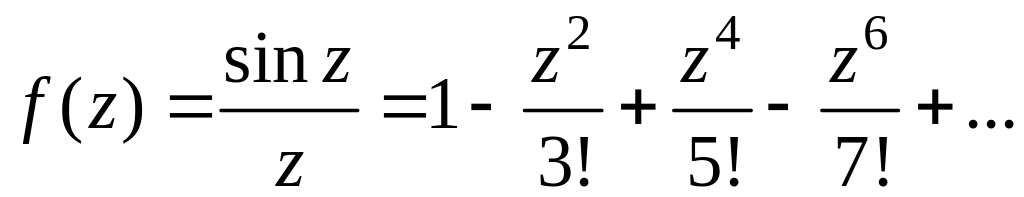Оскільки ряд Лорана заданої функції не містить головної частини, то точка є усувною особливою точкою функції .

в) Для знаходження особливих точок прирівняємо до нуля знаменник дробу.

значить , – особливі точки заданої функції.

Тепер перетворимо задану функцію:

.

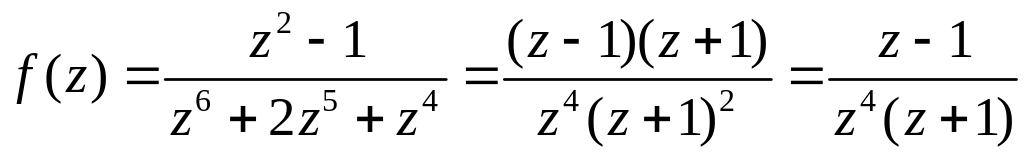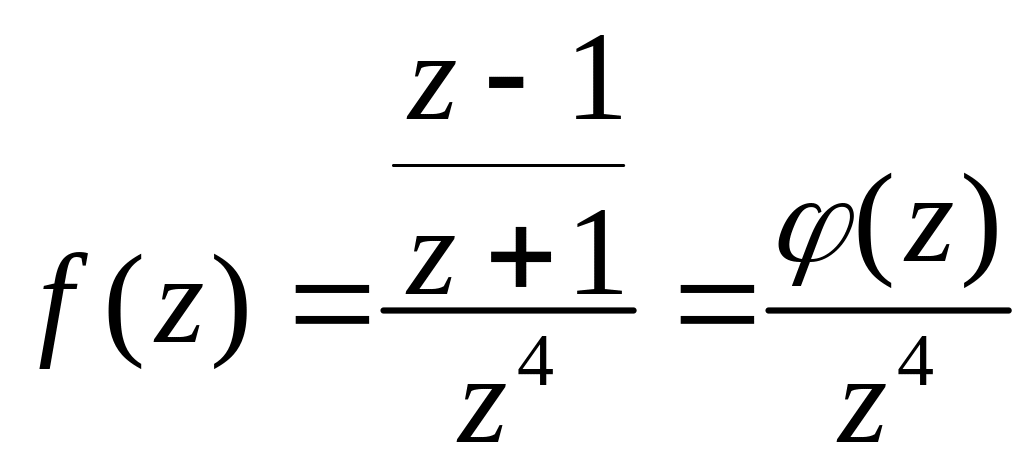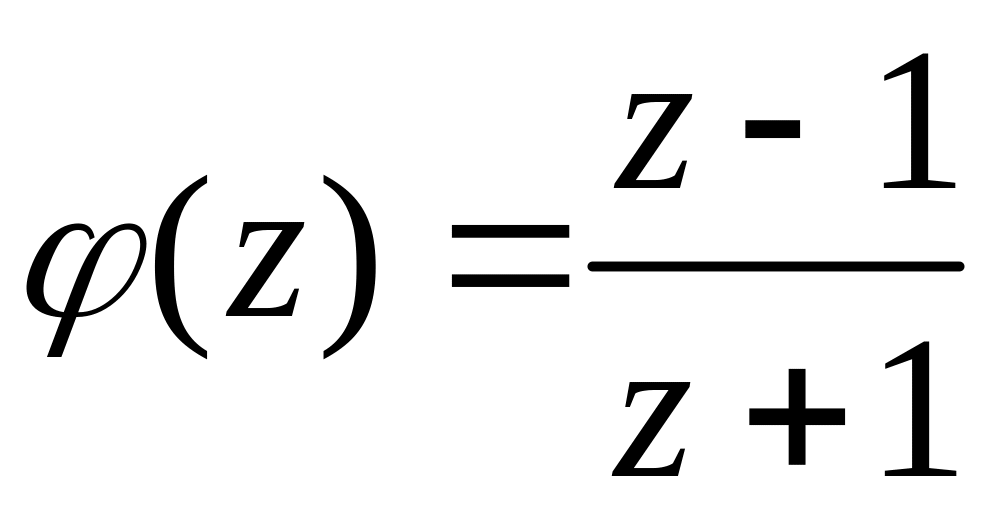Дослідимо точку . Подамо функцію у вигляді , де – аналітична у точці . Значить досліджувана точка є полюсом четвертого порядку заданої функції.

Дослідимо точку . Подамо функцію у вигляд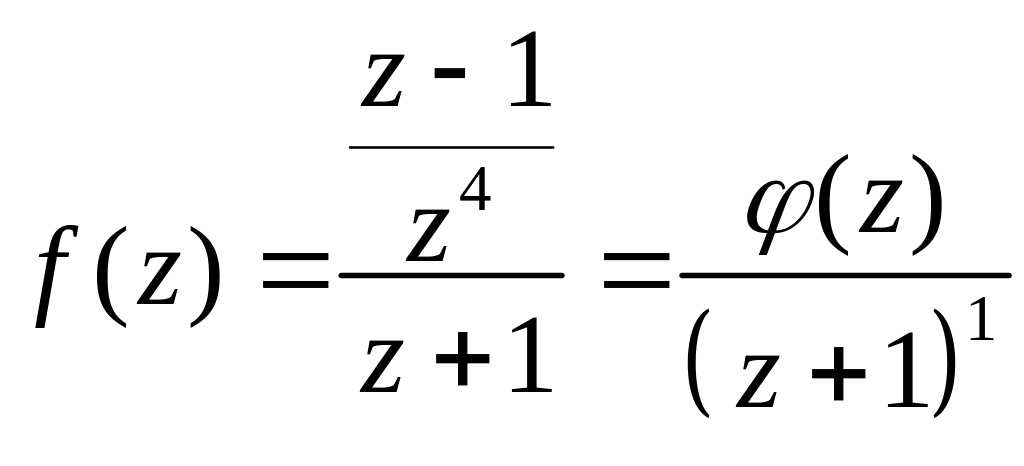і , де – аналітична у точці . Значить досліджувана точка є полюсом першого порідка заданої функції.