
- •Комплексні числа та дії над ними
- •Задачі для самостійного розв'язання
- •Диференційованість функції комплексної змінної, аналітичні функції
- •Задачі для самостійного розв'язання
- •Інтегрування функцій комплексної змінної
- •Задачі для самостійного розв'язання
- •Ряди Лорана, ізольовані особливі точки
- •Задачі для самостійного розв'язання
- •Лишки та їх застосування для обчислення інтегралів
- •Задачі для самостійного розв'язання
Міністерство освіти і науки України
Одеський національний морський університет
Кафедра «Вища та прикладна математика»
Теорія функцій комплексної змінної
Навчальний посібник
Одеса - 2011
Навчальний посібник склали Кирилов Сергій Олександрович – кандидат фізико-математичних наук, доцент кафедри «Вища та прикладна математика» ОНМУ та Войтік Тетяна Геннадіївна, асистент цієї кафедри.
Навчальний посібник схвалений на засіданні кафедри «Вища та прикладна математика» 24 червня 2011 р. (протокол № 10).
Рецензенти: д.ф.-м. н., проф. Андронов І.Л.;
к.ф.-м.н., доц. Григор’єв Ю.О.
Комплексні числа та дії над ними
Комплексним
числом, записаним в алгебраїчній формі
називають вираз виду
![]() ,
де
,
де
![]() і
і
![]() –дійсні числа,
–дійсні числа,
![]() – уявна одиниця, що визначається рівністю
– уявна одиниця, що визначається рівністю
![]() ,
причому
,
причому
![]() називається дійсною частиною, a
називається дійсною частиною, a
![]() – уявною частиною комплексного числа.
– уявною частиною комплексного числа.
Тригонометрична
форма запису комплексного числа має
вигляд
![]() ,
де
,
де
![]() (1)
(1)
– модуль
комплексного числа,
![]() –
аргумент комплексного числа. Кут
–
аргумент комплексного числа. Кут
![]() визначається неоднозначно, з точністю
до доданка, кратного
визначається неоднозначно, з точністю
до доданка, кратного
![]() :
:
![]() .
.
Тут
![]() є головним значенням аргументу, що
визначається умовою
є головним значенням аргументу, що
визначається умовою
![]() .
Для знаходження кута
можна скористатись співвідношеннями
.
Для знаходження кута
можна скористатись співвідношеннями
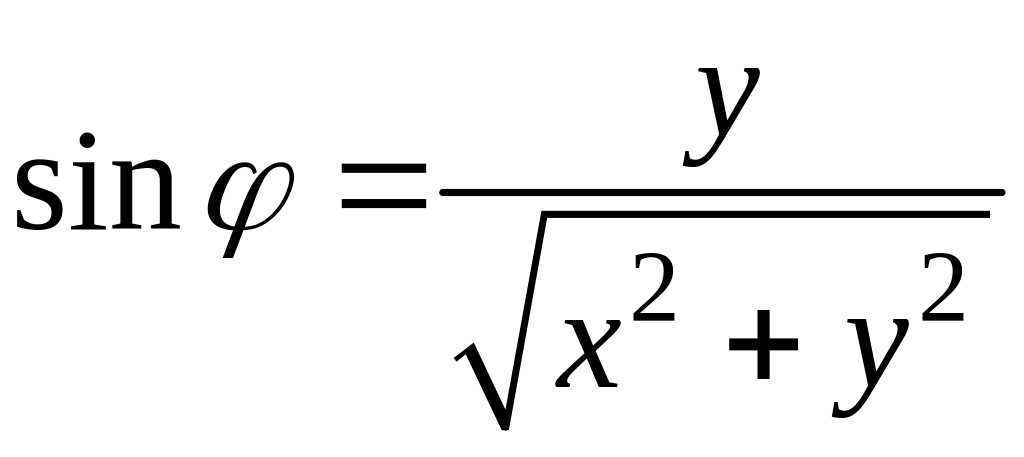 ,
,
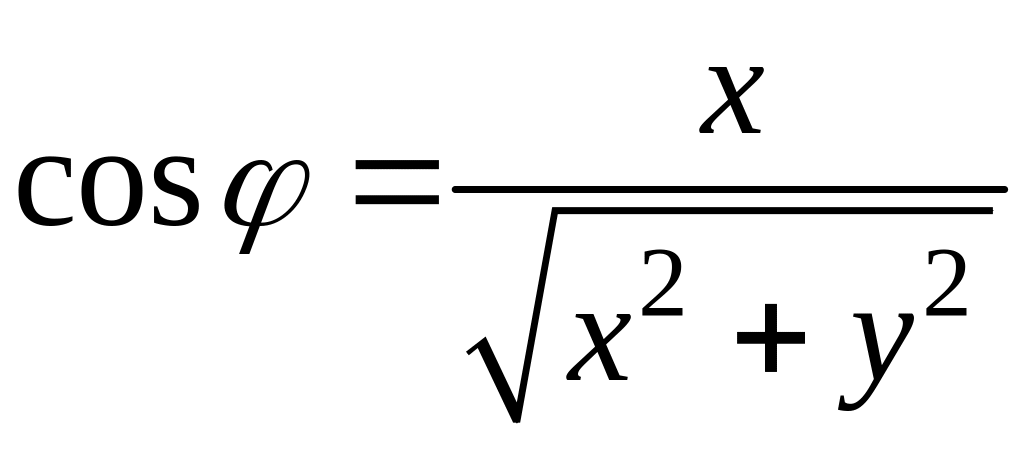 .
(2)
.
(2)
Використовуючи
формулу Ейлера
![]() ,
комплексне число можна також записати
у показниковій формі:
,
комплексне число можна також записати
у показниковій формі:
![]() .
.
Комплексне
число
зображується на комплексній площині
точкою
![]() з координатами
з координатами
![]() .
Модуль
.
Модуль
![]() та аргумент комплексного числа
відповідають полярним координатам
точки
(рис.1).
та аргумент комплексного числа
відповідають полярним координатам
точки
(рис.1).
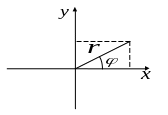
Рис.1
Дії над комплексними числами в алгебраїчній формі.
Нехай
![]() та
та
![]() .
.
1.
Додавання:
![]() .
.
2.
Віднімання:
![]() .
.
3. Множення:
![]() ,
,
тобто множення виконується як звичайне розкриття дужок з урахуванням рівності .
4. Ділення:
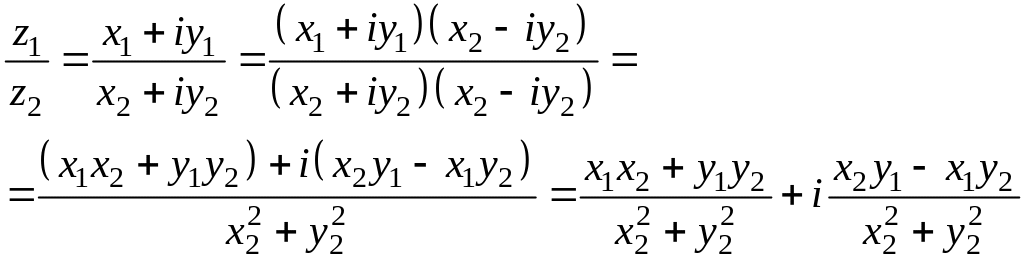 .
.
Дії над комплексними числами в тригонометричній формі.
Нехай .
1. Піднесення до степені:
![]() .
(3)
.
(3)
2. Зволікання кореня:
 ,
де
,
де
![]() (4)
(4)
Задача 1. Записати комплексне число в тригонометричній та показниковій формах.
а)
![]() ;
б)
;
б)
![]() .
.
Розв’язання.
а) Знайдемо модуль комплексного числа
за формулою (1):
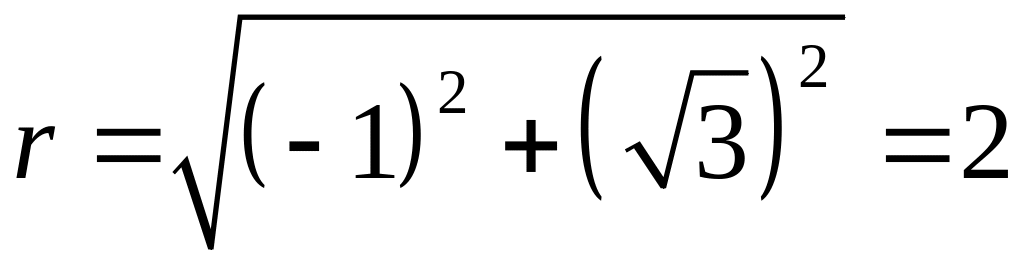 .
Тепер знайдемо аргумент, використавши
рівності (2):
.
Тепер знайдемо аргумент, використавши
рівності (2):
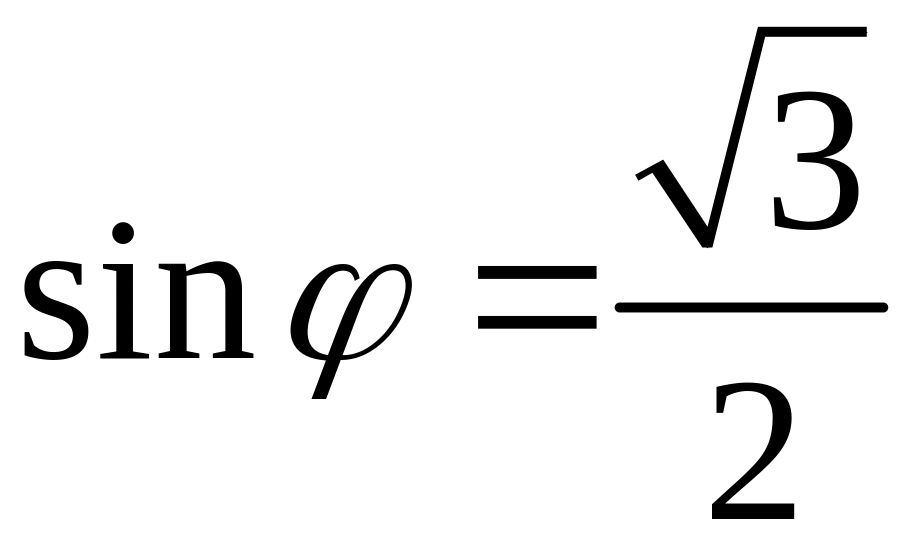 ,
,
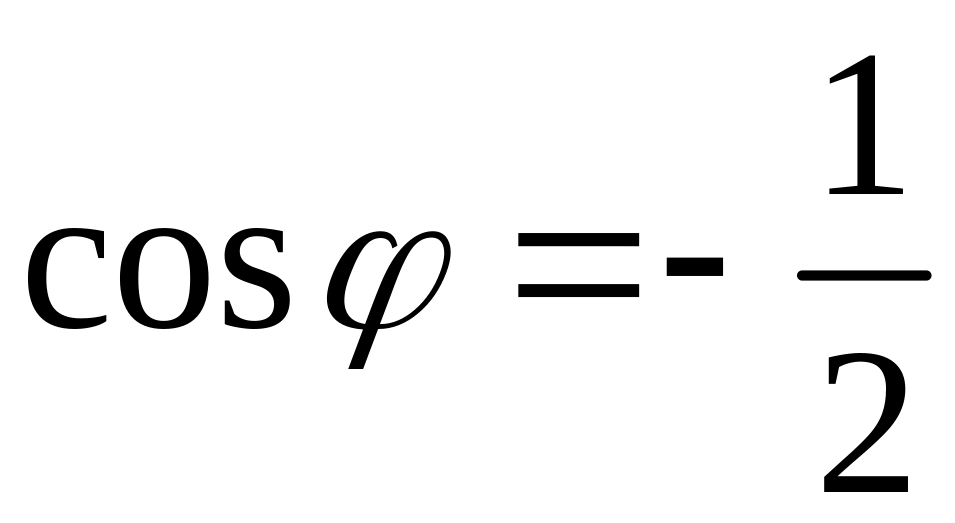 ,
тобто
,
тобто
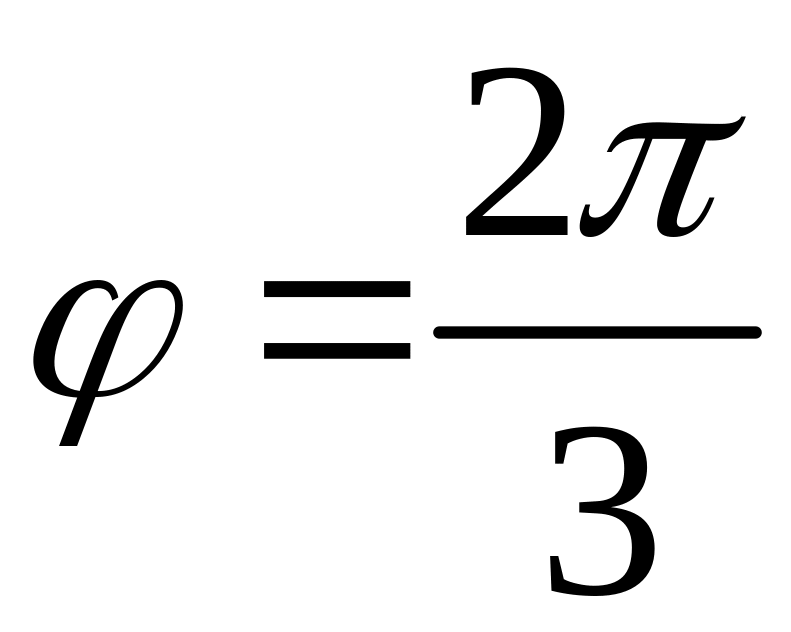 (рис. 2). Остаточно маємо:
(рис. 2). Остаточно маємо:
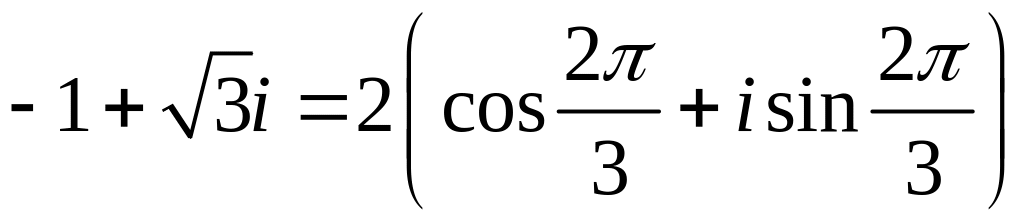 у тригонометричній формі та
у тригонометричній формі та
![]() у показниковій формі.
у показниковій формі.
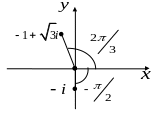
Рис.2
б)
Знайдемо модуль комплексного числа:
![]() .
Тепер знайдемо аргумент:
.
Тепер знайдемо аргумент:
![]() ,
,
![]() ,
тобто
,
тобто
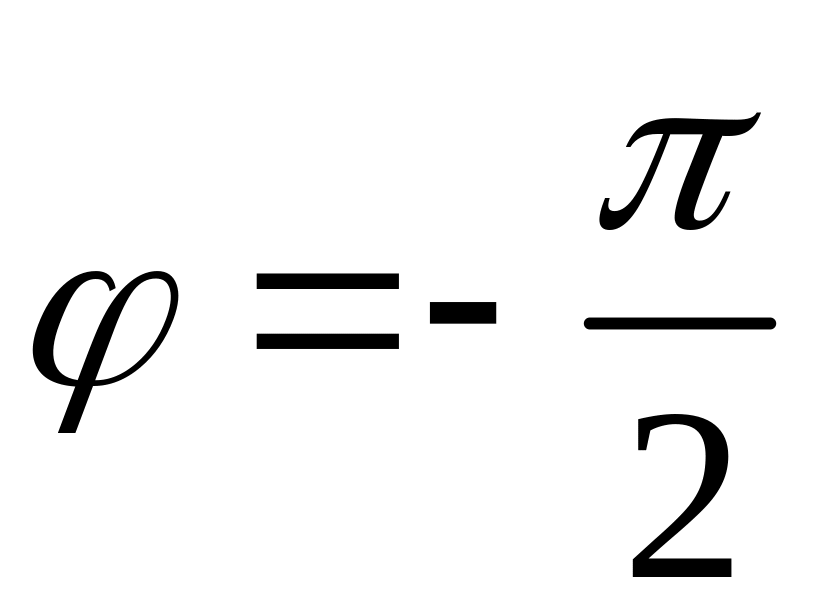 (рис. 2). Відповідно одержимо:
(рис. 2). Відповідно одержимо:
 у тригонометричній формі та
у тригонометричній формі та
![]() у показниковій формі.
у показниковій формі.
Задача 2. Виконати дії над комплексними числами:
а)
![]() ;
б)
;
б)
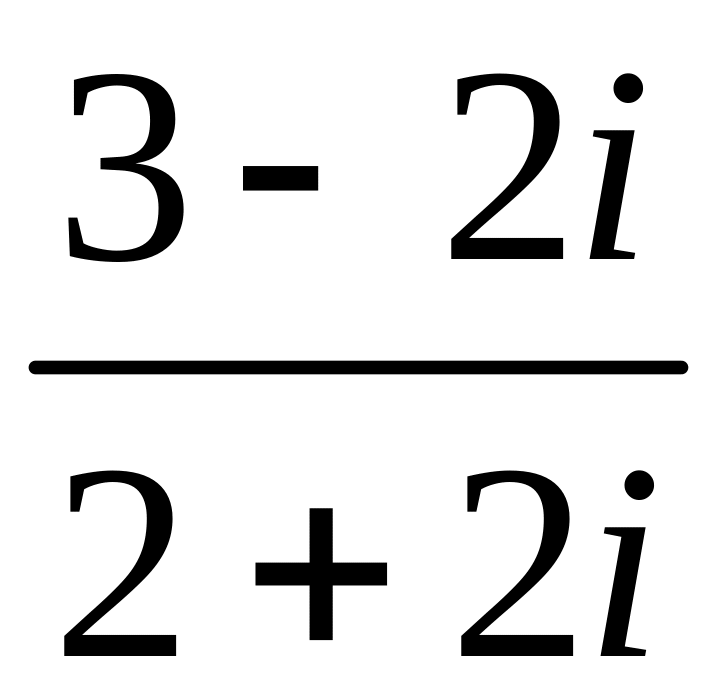 ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Розв’язання.
а)
![]() .
.
б)
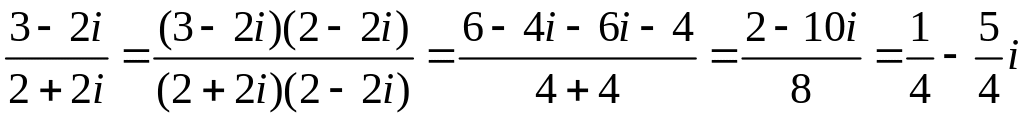 .
.
в)
Подамо число
![]() в тригонометричній формі. Знайдемо
модуль комплексного числа:
в тригонометричній формі. Знайдемо
модуль комплексного числа:
![]() .
Тепер знайдемо аргумент:
.
Тепер знайдемо аргумент:
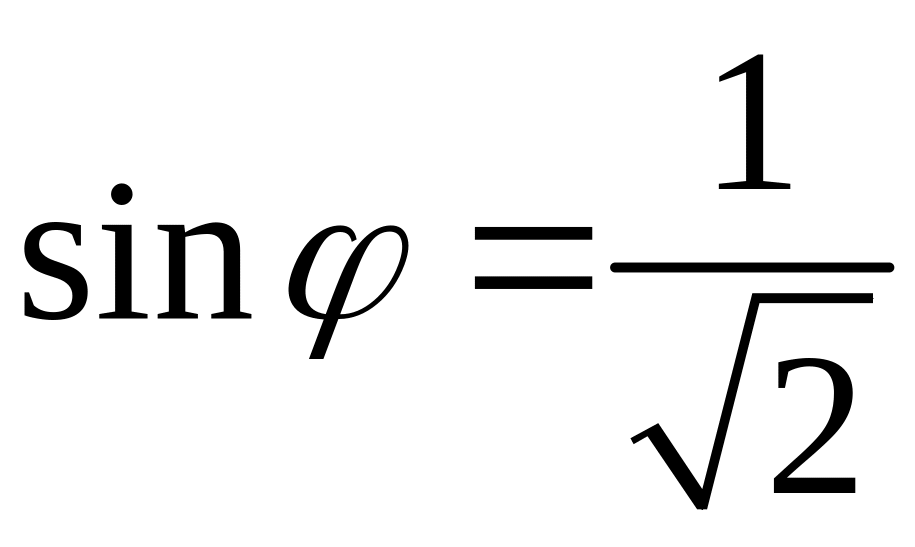 ,
,
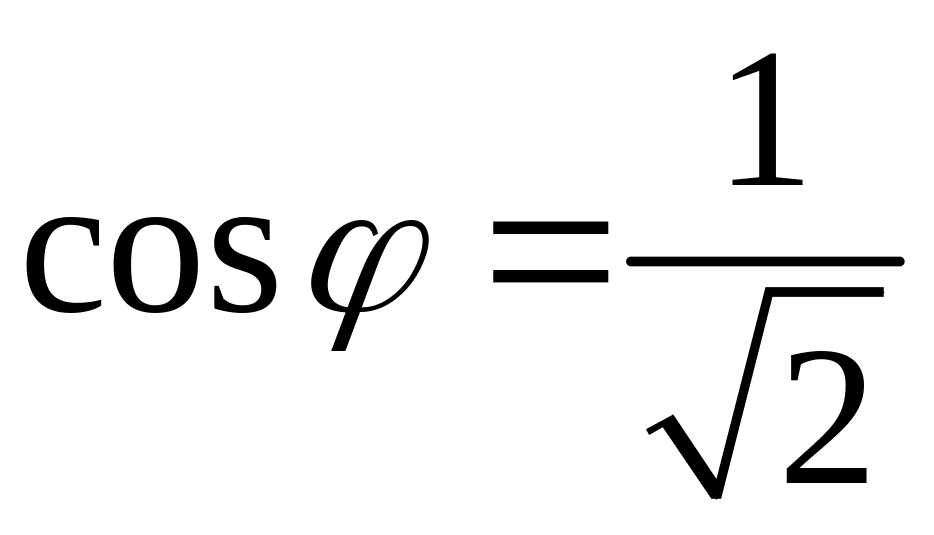 ,
тобто
,
тобто
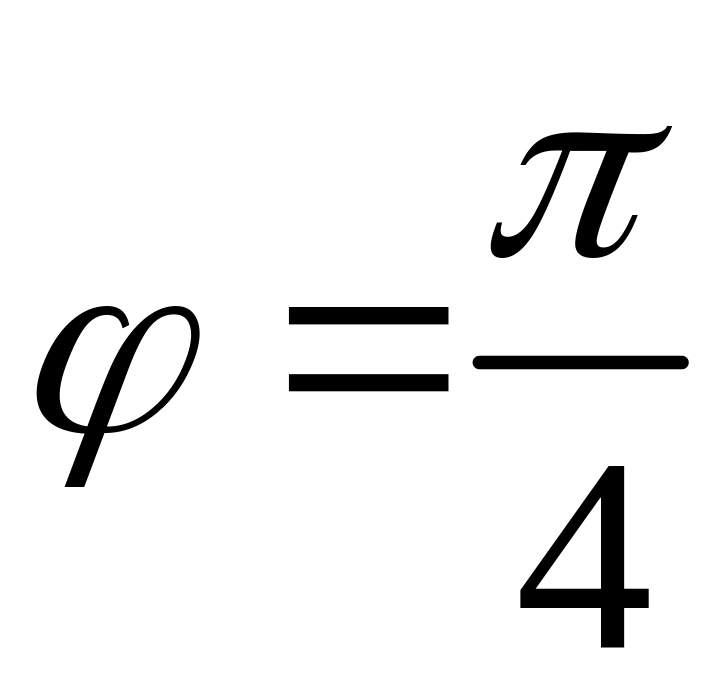 .
Остаточно маємо:
.
Остаточно маємо:
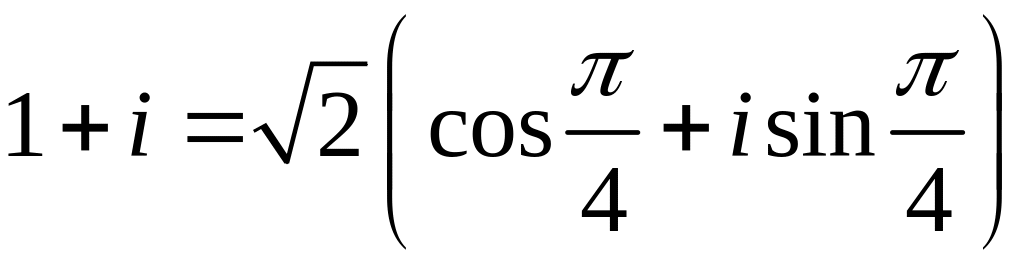 .
Тепер скористаємось формулою (3).
.
Тепер скористаємось формулою (3).
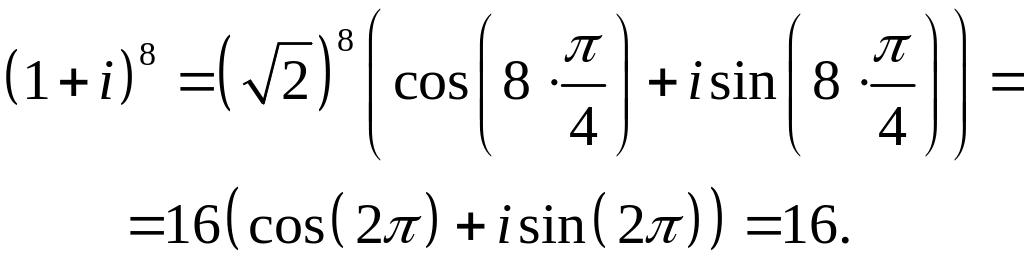
г)
Подамо число
![]() в тригонометричній формі. Знайдемо
модуль комплексного числа:
.
Тепер знайдемо аргумент:
в тригонометричній формі. Знайдемо
модуль комплексного числа:
.
Тепер знайдемо аргумент:
![]() ,
,
![]() ,
тобто
,
тобто
![]() .
Остаточно маємо:
.
Остаточно маємо:
![]() .
Тепер скористаємось формулою (4). Одержимо
чотири значення кореня.
.
Тепер скористаємось формулою (4). Одержимо
чотири значення кореня.
При
![]() .
.
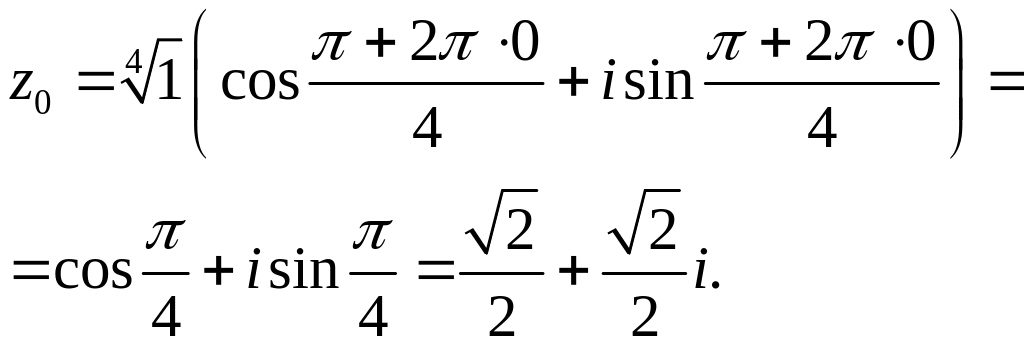
При
![]() .
.
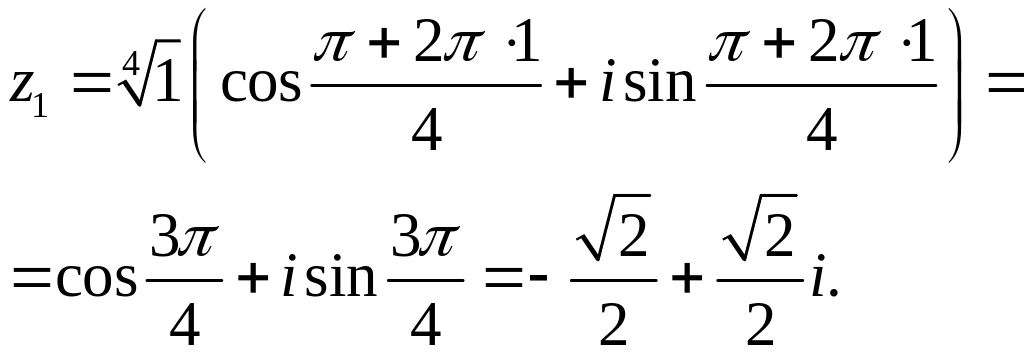
При
![]() .
.
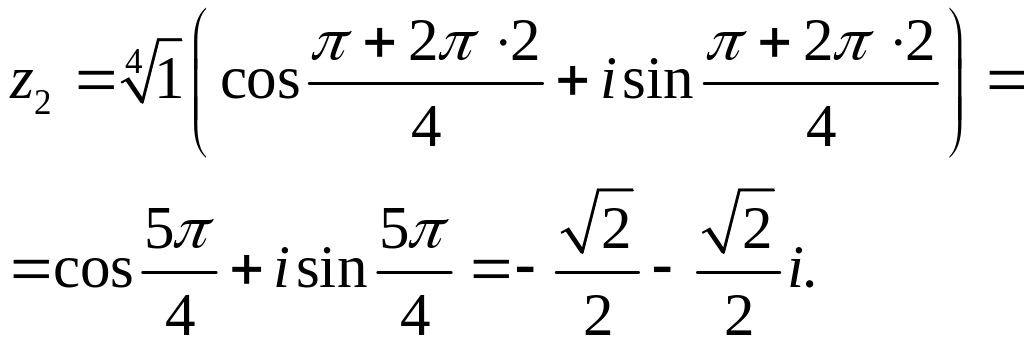
При
![]() .
.
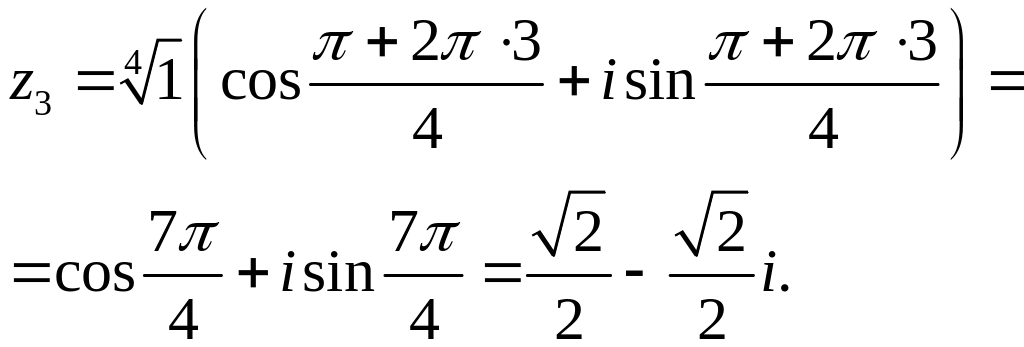
Задачі для самостійного розв'язання
1. Подати комплексне число у тригонометричній та показниковій формах.
а) ; б) ; в) ; г) .
2. Виконати дії над комплексними числами.
а) ; б) ; в) ; г) .
Диференційованість функції комплексної змінної, аналітичні функції
Для
того, щоб функція
![]() була диференційованою у точці
,
необхідно і достатньо, щоб функції
була диференційованою у точці
,
необхідно і достатньо, щоб функції
![]() та
та
![]() були диференційованими у точці
,
як функції двох змінних, та виконувались
умови Коші-Рімана:
були диференційованими у точці
,
як функції двох змінних, та виконувались
умови Коші-Рімана:
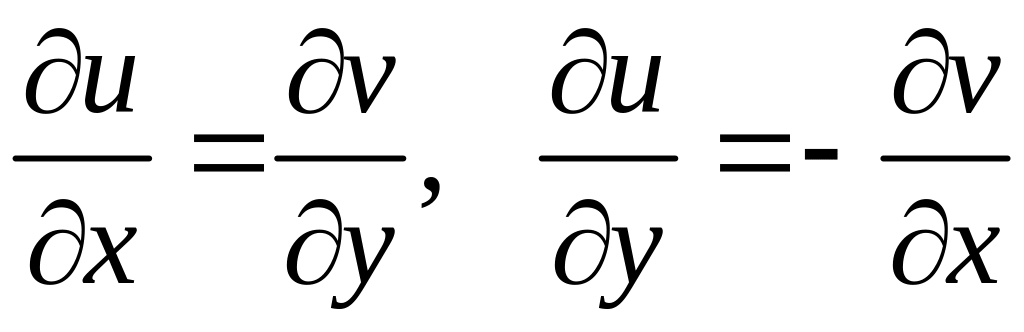 .
(5)
.
(5)
Якщо умови Коші-Рімана виконані, то похідна визначається формулами
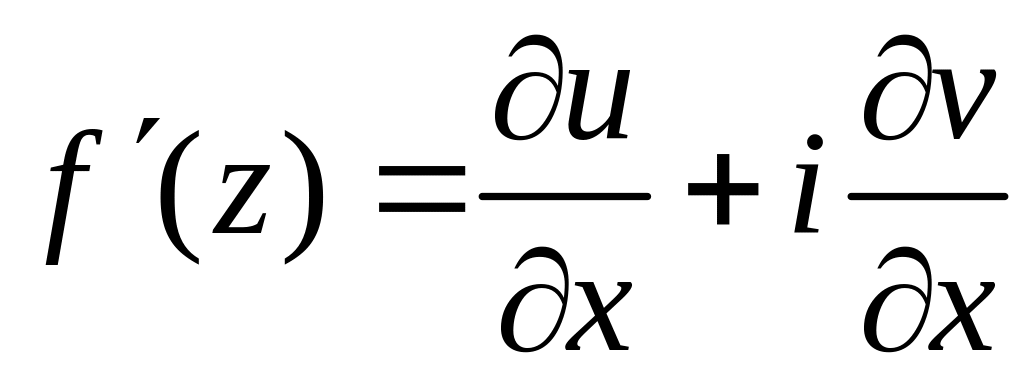 або
або
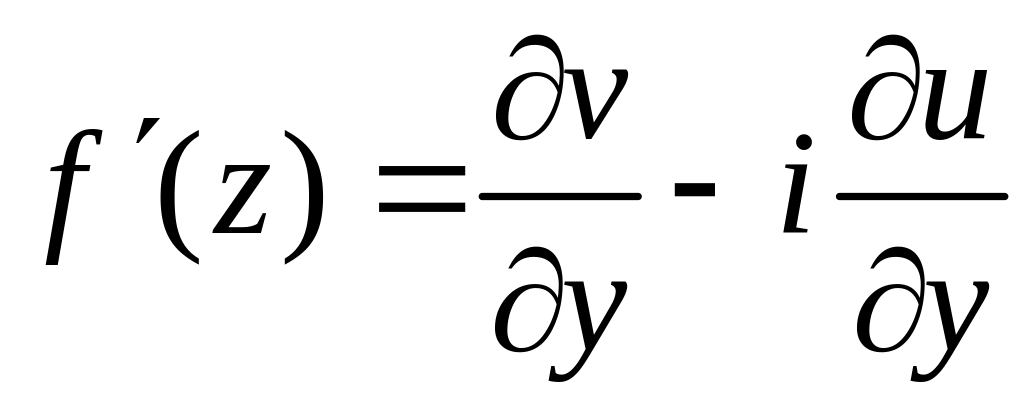 .
.
Якщо
функція
однозначна та диференційована у кожній
точці області
![]() ,
то вона називається аналітичною у цій
області.
,
то вона називається аналітичною у цій
області.
Задача 3. Дослідити функції на диференційованість.
а)
![]() ;
б)
;
б)
![]() .
.
Розв’язання.
а) Нехай . Тоді
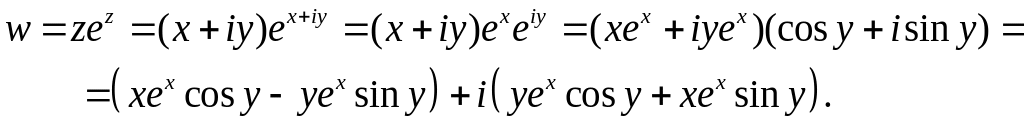
Значить
![]() та
та
![]() .
Тепер
перевіримо умови Коші-Рімана (5).
.
Тепер
перевіримо умови Коші-Рімана (5).
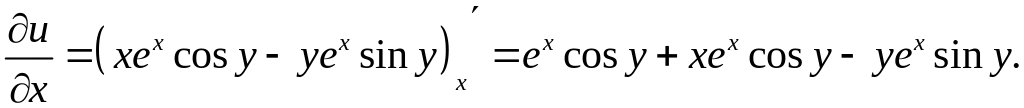
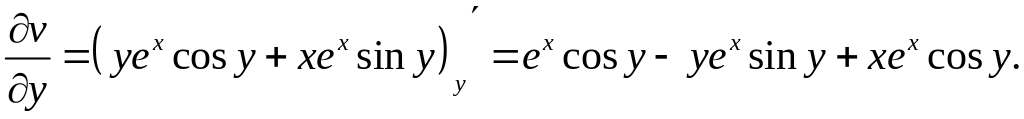
Значить
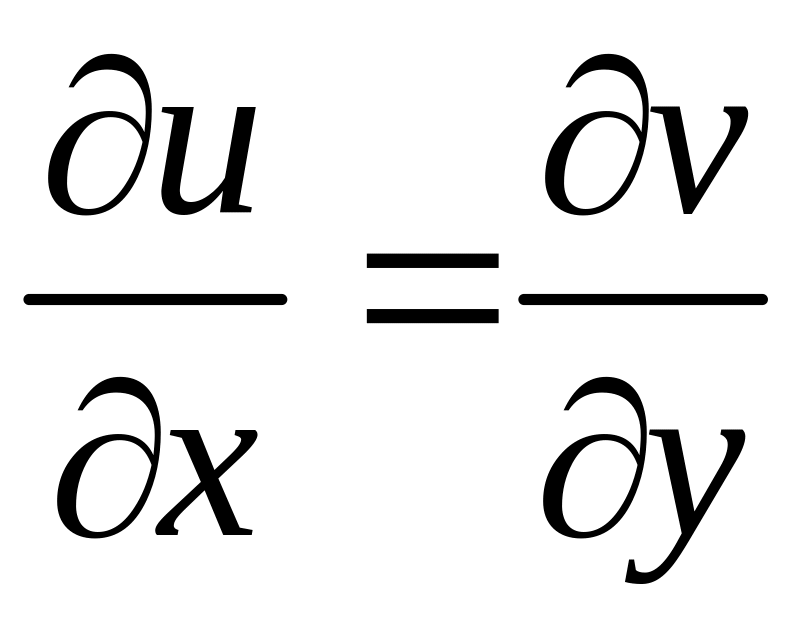 .
.
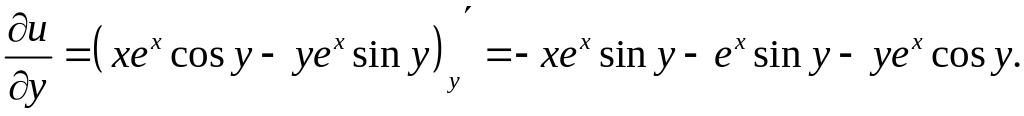
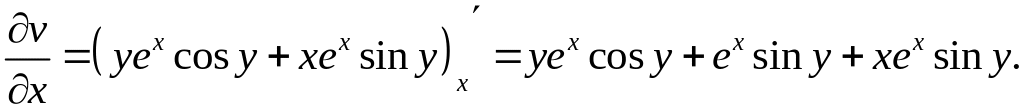
Значить
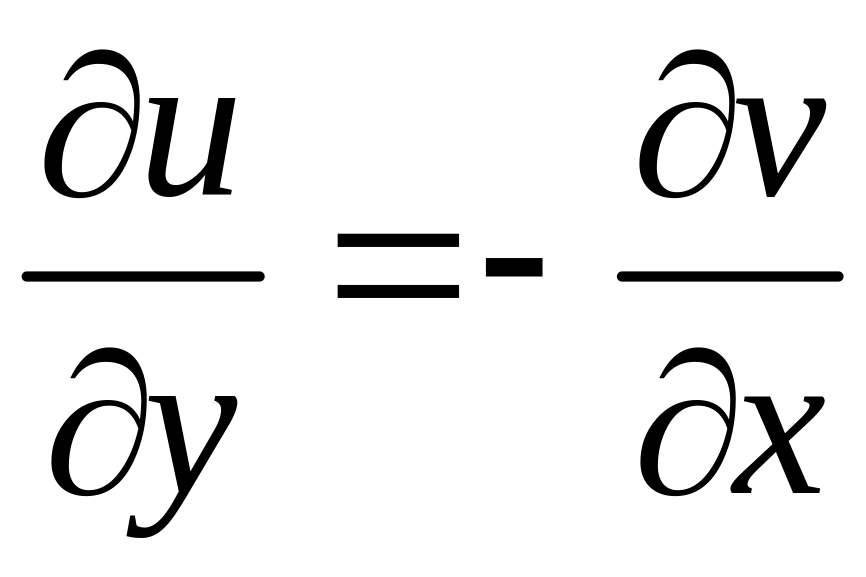 .
Умови Коші-Рімана виконуються, тобто
функція є диференційованою.
.
Умови Коші-Рімана виконуються, тобто
функція є диференційованою.
б) Нехай . Тоді
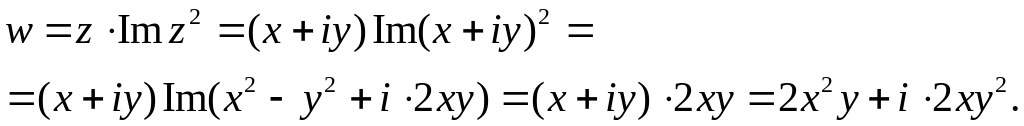
Значить
![]() та
та
![]() .
Тепер
перевіримо умови Коші-Рімана (5).
.
Тепер
перевіримо умови Коші-Рімана (5).
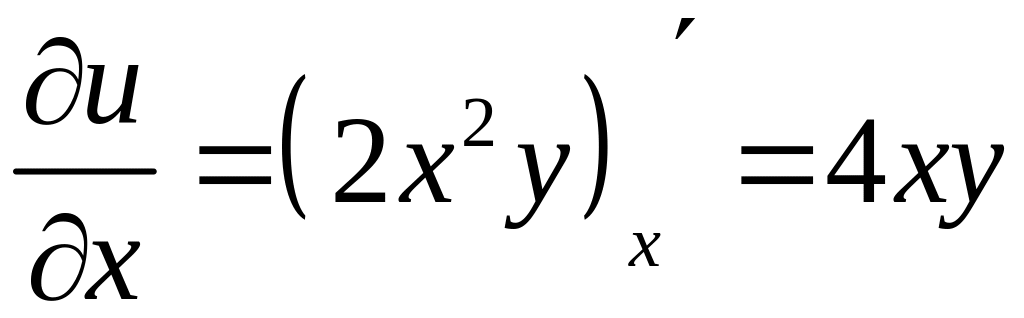 ,
,
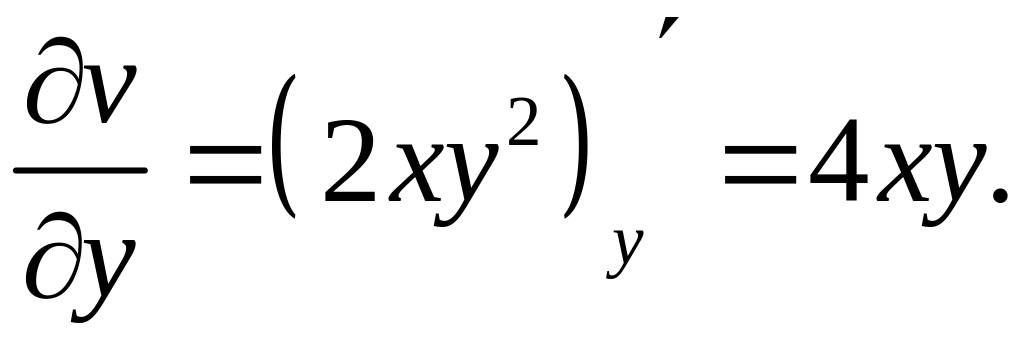 Значить
.
Значить
.
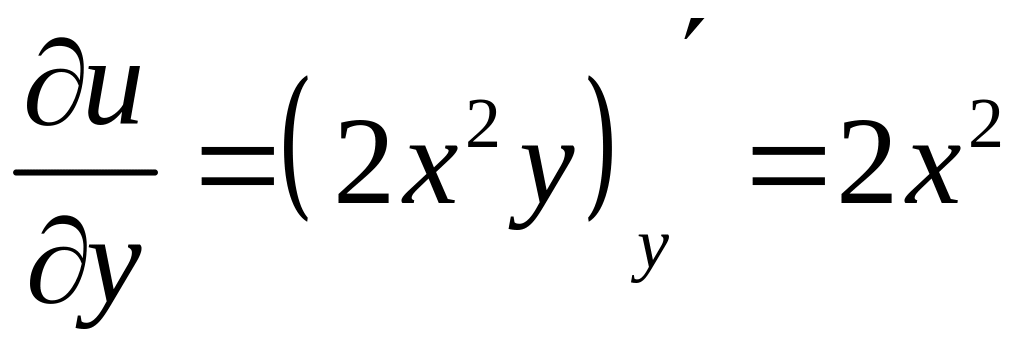 ,
,
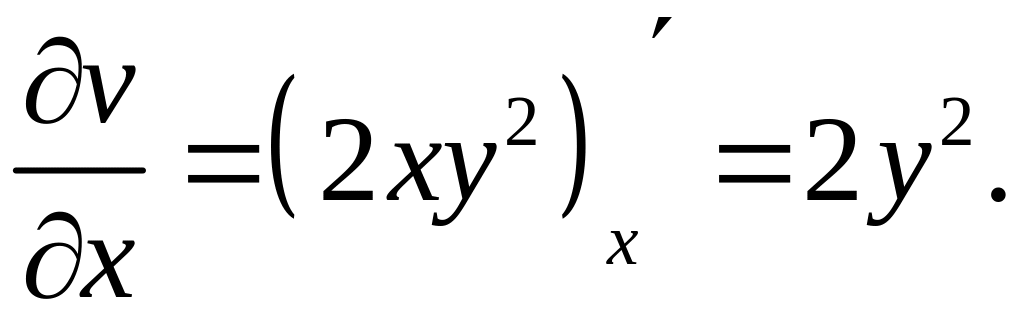 Значить
Значить
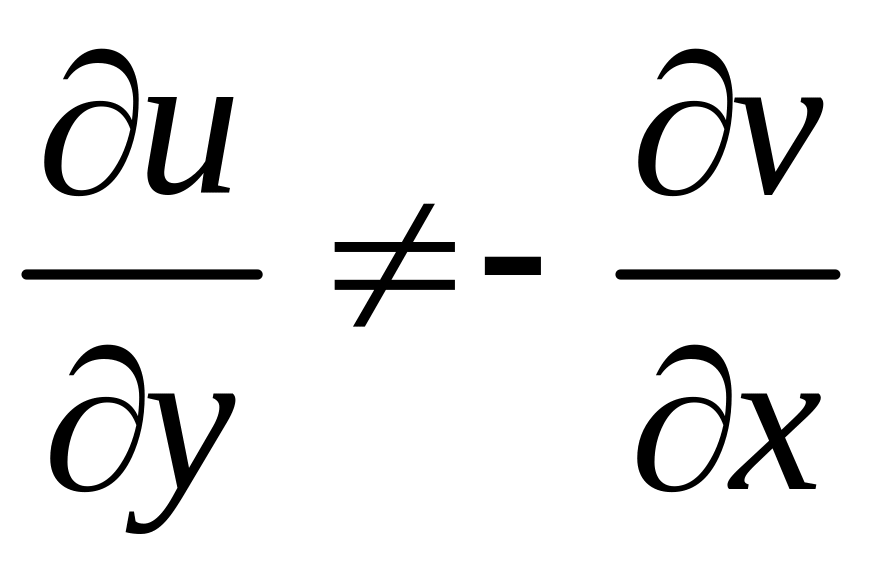 .
.
Умови Коші-Рімана не виконуються, значить функція не є диференційованою.
Задача
4.
Знайти аналітичну функцію
![]() якщо відомі:
якщо відомі:
а)
її уявна частина
![]() за умови, що
за умови, що
![]() ;
;
б)
її дійсна частина
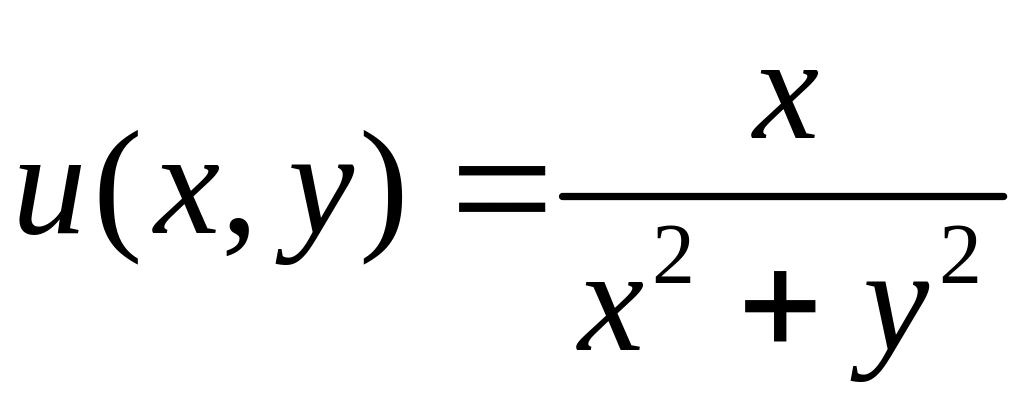 за умови, що
за умови, що
![]() .
.
Розв’язання. а) Знайдемо:
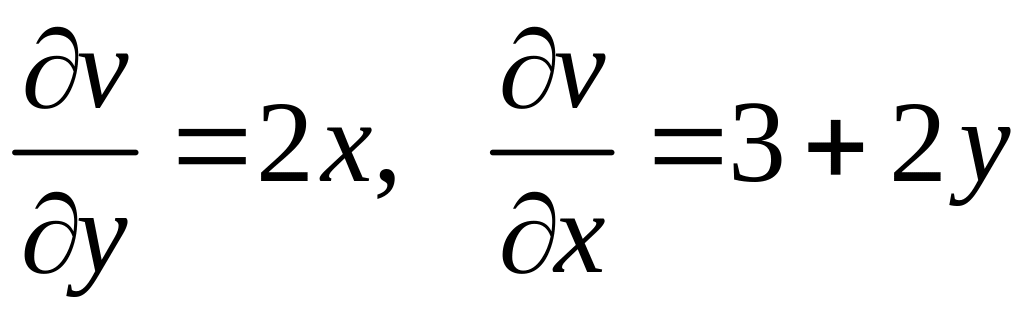 .
.
З
(5) виходить, що
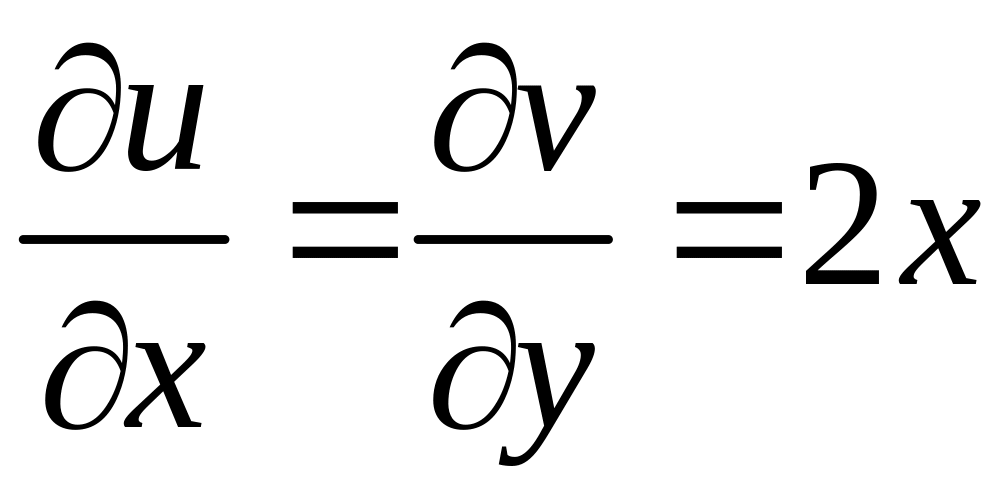 .
Тоді
.
Тоді
![]() .
.
Знову використаємо умови Коші Рімана:
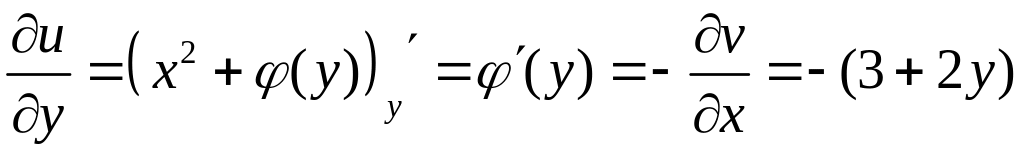 .
.
Інтегруємо одержану рівність:
![]() .
.
Значить
![]() .
Тому
.
Тому
![]() .
.
З
умови
одержимо рівність (![]() ,
тобто можна вважати
,
тобто можна вважати
![]() ):
):
![]() .
.
Звідси
![]() .
Остаточно одержимо
.
Остаточно одержимо
![]() .
.
б) Знайдемо:
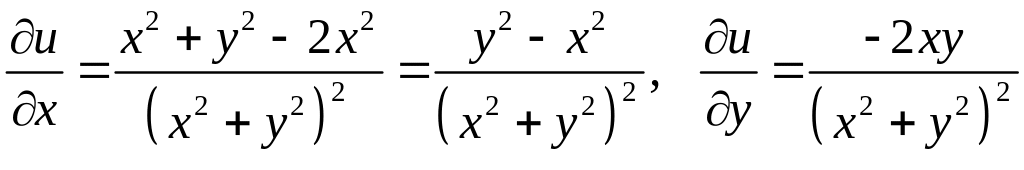 .
.
З
(5) виходить, що
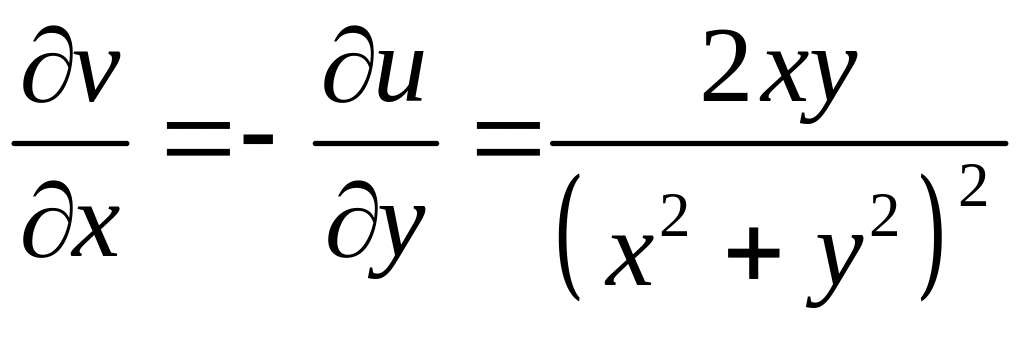 .
Тоді
.
Тоді
 .
.
Знову використаємо умови Коші Рімана:
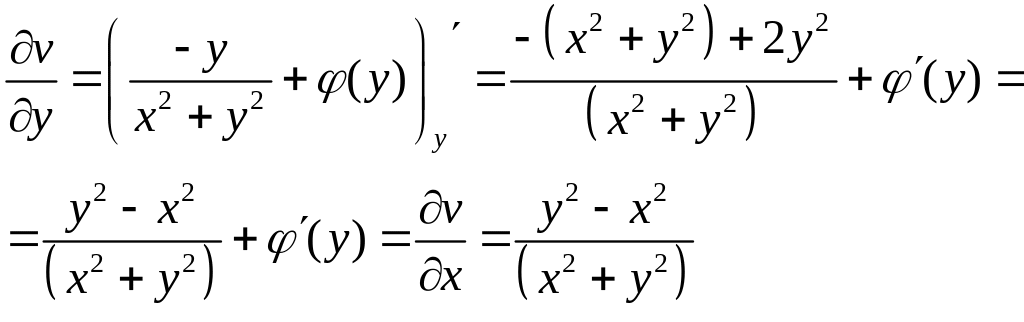 .
.
Звідси
![]() .
.
Інтегруємо одержану рівність:
![]() .
.
Значить
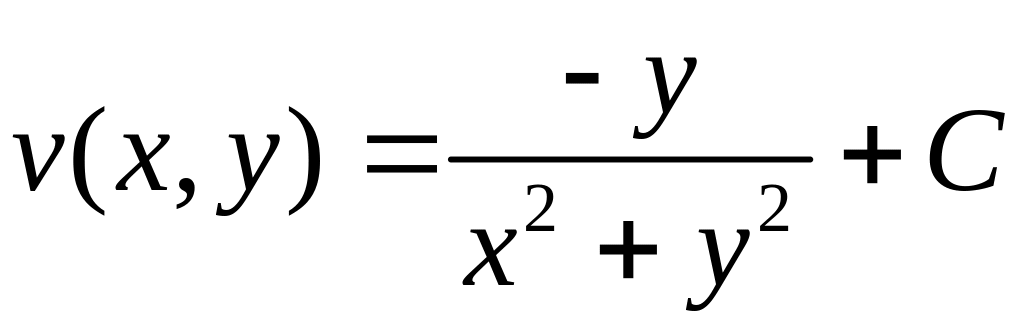 .
Тому
.
Тому
 .
.
З
умови
одержимо рівність (![]() ,
тобто можна вважати
,
тобто можна вважати
![]() ):
):
![]() .
.
Звідси
![]() .
Остаточно одержимо
.
Остаточно одержимо

