20. Энергия гармонических колебаний.

 При механических колебаниях колеблющееся тело (или материальная точка) обладает кинетической и потенциальной энергией. Кинетическая энергия тела W:

Для вычисления потенциальной энергии тела воспользуемся самой общей формулой, связывающей силу и потенциальную энергию тела в поле этой силы:

где U - потенциальная энергия, набираемая (или теряемая) телом, движущимся в силовом поле F от точки 0 (точки, в которой потенциальная энергия принимается равной 0) до точки х.

Для силы, линейно зависящей от смещения (как в случае наших механических маятников, такие силы носят общее название квазиупругих сил) мы имеем:

Сравнивая формулы для кинетической и потенциальной энергии механического маятника, можно сделать следующие выводы:

1. Полная механическая энергия тела не изменяется при колебаниях:

2. Частота колебаний кинетической и потенциальной энергии в 2 раза больше частоты колебаний маятника.

3. Колебания кинетической и потенциальной энергии сдвинуты друг относительно друга по фазе на π (на полпериода). Когда кинетическая энергия достигает максимума, потенциальная - минимума (нуля) и наоборот. Энергия при колебаниях постоянно перекачивается из потенциальной в кинетическую и обратно.

21. Сложение гармонических колебаний с одинаковой амплитудой и близкими частотами (биения).

БИЕНИЯ - периодические изменения во времени амплитуды колебания, возникающего при сложении двух гармонических колебаний с близкими частотами. Биения появляются вследствие того, что величина разности фаз между двумя колебаниями с различными частотами всё время изменяется так, что оба колебания оказываются в какой-то момент времени в фазе, через некоторое время в противофазе, затем снова в фазе и т.д. Соответственно амплитуда результирующего колебания периодически достигает то максимума, равного сумме амплитуд складываемых колебаний, то минимума, равного разности этих амплитуд (рис.). Напр., биения возникают при звучании двух камертонов с близкими частотами - звук поочерёдно усиливается и ослабевает, при сложении нормальных колебаний с близкими частотами в связанных линейных осцилляторах.

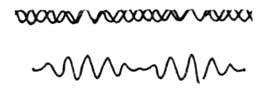
Биения, возникающие в результате сложения двух гармонических колебаний с одинаковыми амплитудами и близкими частотами.

При сложении двух бегущих в одном направлении волн с близкими частотами и волновыми числами биения возникают не только во времени, но и в пространстве. Складывая, напр., волны с равными амплитудами

Получаем результирующую волну

22. Волны в упругой среде. Поперечные и продольные волны. Уравнение бегущей волны.

Если в каком-либо месте упругой (твердой, жидкой или газообразной) среды возбудить колебания ее частиц, то вследствие взаимодействия между частицами это колебание будет распространяться в среде от частицы к частице с некоторой скоростью v. Процесс распространения колебаний в пространстве называется волной.

Частицы среды, в которой распространяется волна, не вовлекаются волной в поступательное движение, они лишь совершают колебания около своих положений равновесия. В зависимости от направления колебаний частиц по отношению к направлению, в котором распространяется волна, различают продольные и поперечные волны. В продольной волне частицы среды колеблются вдоль направления распространения волны. В поперечной волне частицы среды колеблются в направлениях, перпендикулярных к направлению распространения волны. Упругие поперечные волны могут возникнуть лишь в среде, обладающей сопротивлением сдвигу.

Продольные волны могут возбуждаться в средах, в которых возникают упругие силы при деформации сжатия и растяжения, т. е. твердых, жидких и газообразных телах. Поперечные волны могут возбуждаться в среде, в которой возникают упругие силы при деформации сдвига, т. е. в твердых телах; в жидкостях и газах возникают только продольные волны, а в твердых телах — как продольные, так и поперечные.

Уравнение волны и основные характеристики

 – уравнение волны, волна распространяется вдоль ось Ох.

k- волновое число, оно показывает сколько раз укладывается х в нем.

 - длина волны. Длина волны – это минимальное расстояние между точками, которые колеблются в одинаковой фазе.

 - скорость распространения волны

 - частота колебаний

 - циклическая частота

Т – период колебания

 Уравнение плоской одномерной синусоидальной волны:

Вместо синуса можно написать косинус.) Это уравнение отличается от уравнения синусоидальных колебаний тем, что колеблющая величина S зависит не только от времени, но и от координаты. Это и понятно: вместо одного маятника мы имеем множество связанных маятников - частиц среды. v - скорость распространения волны, А - амплитуда волны, аргумент синуса - фаза волны,   - начальная фаза колебаний в точке х = 0,   - частота (циклическая) волны.

Расстояние, на которое распространяется волна за время, равное периоду колебаний, называется ДЛИНОЙ ВОЛНЫ .

ВОЛНОВОЕ ЧИСЛО k:

С помощью введенного волнового числа уравнение волны запишется:

Если мы рассматриваем не одномерную волну, удобно наряду с волновым числом ввести ВОЛНОВОЙ ВЕКТОР k, модуль которого равен волновому числу, а направление совпадает с направлением луча (направлением распространения волны). В векторном виде уравнение волны будет выглядеть так:

здесь r - радиус вектор точки пространства;   - начальная фаза колебаний в начале координат.