18. Гармонические колебания и их характеристики. Дифференциальное уравнение гармонических колебаний.

Гармонические колебания — колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (косинуса). Исследование гармонических колебаний важно по двум причинам: 1) колебания, которые встречаются в природе и технике, часто имеют близкий к гармоническому характер; 2) различные периодические процессы (процессы, которые повторяются через равные промежутки времени) можно представить как суперпозицию (наложение) гармонических колебаний. Гармонические колебания некоторой величины описываются уравнением вида 

где x - смещение точки от положения равновесия, величина x может принимать значения, лежащие в пределах от -A до +A

А – амплитуда колебаний (величина наибольшего отклонения системы от положения равновесия); ₀ - круговая (циклическая) частота.

Периодически изменяющийся аргумент косинуса – называется фазой колебаний. Фаза колебаний определяет смещение колеблющейся величины от положения равновесия в данный момент времени t. Постоянная представляет собой значение фазы в момент времени t = 0 и называется начальной фазой колебания.

Промежуток времени T, через который повторяются определенные состояния колебательной системы, называется периодом колебаний.

Косинус - периодическая функция с периодом 2π, поэтому за промежуток времени T, через который фаза колебаний получит приращение равное 2π, состояние системы, совершающей гармонические колебания, будет повторяться. Этот промежуток времени T называется периодом гармонических колебаний.

Период гармонических колебаний равен: T = 2π/₀. Число колебаний в единицу времени называется частотой колебаний ν. Частота гармонических колебаний равна: ν = 1/T. Единица измерения частоты герц (Гц) - одно колебание в секунду. Круговая частота ₀ = 2π/T = 2πν дает число колебаний за 2π секунд.

Графически гармонические колебания можно изображать в виде зависимости x от t, так и методом вращающейся амплитуды (метод векторных диаграмм)

Дифференциальное уравнение гармонических колебаний

(1)

Скорость   колеблющейся материальной точки получим, продифференцировав (1)по времени:

(2)

Продифференцировав (2), получим ускорение а:

(3)

19. Пружинный, физический и математический маятники.

Пружинный маятник это груз, прикрепленный к пружине, массой которой можно пренебречь.

Пока пружина не деформирована, сила упругости на тело не действует. В пружинном маятнике колебания совершаются под действием силы упругости.

Математический маятник – это материальная точка, подвешенная на тонкой нерастяжимой и невесомой нити.

Если отклонить маятник от положения равновесия, то сила тяжести и сила упругости будут направлены под углом. Равнодействующая сила уже не будет равна нулю. Под воздействием этой силы маятник устремится к положению равновесия, но по инерции движение продолжится и маятник отклоняется в другую сторону. Равнодействующая сила его снова возвращает. Далее процесс повторяется.

Период колебаний математического маятника зависит от его длины, определяется по формуле

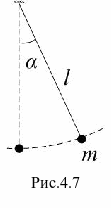
Важно где происходят колебания! На Луне и на Земле один и тот же математический маятник при одинаковых начальных условиях колебаться будет по-разному. Так как ускорение свободного падения на Луне отличается от ускорения свободного падения на Земле.

Физическим маятником называется твёрдое тело, способное колебаться в поле силы тяжести относительно оси, не проходящей через центр масс.

Длина физического маятника   – это расстояние между центром масс С и осью вращения (точка О). Плечо силы тяжести равно где   – угол отклонения из положения равновесия. Момент силы тяжести относительно оси вращения. Период колебаний физического маятника ,где _ приведенная длина физического маятника (длина такого математического маятника, который имеет такой же период колебаний, что и данный физический маятник).