47. Вектор электрического смещения. Теорема Остроградского-Гаусса для электростатического поля в диэлектриках.

Напряженность электростатического поля, согласно, зависит от свойств среды: в однородной изотропной среде напряженность поля Е обратно пропорциональна ε. Вектор напряженности  , переходя через границу диэлектриков, претерпевает скачкообразное изменение, создавая тем самым неудобства при расчетах электростатических полей. Поэтому оказалось необходимым помимо вектора напряженности характеризовать поле еще вектором электрического смещения, который для электрически изотропной среды, по определению, равен .

Электрическое смещение – векторная величина, она не зависит от свойств среды. Таки образом, электрическое смещение внутри однородного диэлектрика совпадает с электрическим смещением внешнего поля, т.е. вакуума. Электрическое смещение, создаваемое в данной точке поля системой электрических зарядов, равно геометрической сумме векторов электрического смещения, создаваемых в этой точке каждым зарядом в отдельности .

Линии электрического смещения – это линии, касательные к которым в каждой точке совпадают по направлению с вектором электрического смещения .

Теорема Гаусса для электростатического поля в диэлектрике:

т. е. поток вектора смещения электростатического поля в диэлектрике сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности свободных электрических зарядов. В такой форме теорема Гаусса справедлива для электростатического поля как для однородной и изотропной, так и для неоднородной и анизотропной сред.

Для вакуума D_n = ε ₀E_n (ε =1), тогда поток вектора напряженности  сквозь произвольную замкнутую поверхность равен .

Так как источниками поля   в среде являются как свободные, так и связанные заряды, то теорему Гаусса для поля   в самом общем виде можно записать как

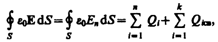
де  и  — соответственно алгебраические суммы свободных и связанных зарядов, охватываемых замкнутой поверхностью S.

Однако эта формула неприемлема для описания поля   в диэлектрике, так как она выражает свойства неизвестного поля   через связанные заряды, которые, в свою очередь, определяются им же. Это еще раз доказывает целесообразность введения вектора электрического смещения.

48. Проводники в электростатическом поле. Распределение зарядов в проводниках. Поле внутри проводника и на его поверхности.

Проводники отличаются от диэлектриков наличием свободных носителей заряда. В металлических проводниках роль этих носителей выполняют свободные электроны, концентрация которых составляет приблизительно и они способны перемещаться под действием самой малой силы. Для того чтобы заряды оставались в равновесии необходимо выполнение следующих условий:

1. Напряженность электрического поля внутри проводника должна быть равной нулю:

.

Потенциал внутри проводника должен быть постоянным ( ).

2. На поверхности проводника силовые линии и вектор напряженности электрического поля должны быть направлены перпендикулярно к поверхности проводника:

Это условие означает, что поверхность проводника в условиях равновесия является эквипотенциальной. В противном случае электроны двигались бы вдоль поверхности проводника.

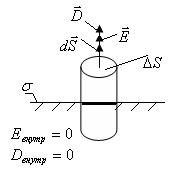
Электрические заряды располагаются на поверхности проводника с некоторой плотностью  , создают вне проводника электрическое поле. Представим небольшую цилиндрическую поверхность, образованную нормалями к поверхности проводника и достаточно малыми основаниями  , одно из которых располагается внутри, а другое вне проводника. Поток вектора электрического смещения   через внутреннюю часть поверхности равен нулю, так как внутри проводника  , а значит  .

Вне проводника в непосредственной близости к нему напряженность   направлена по нормали к поверхности  , а значит  . Теорема Гаусса для вектора   (над поверхностью проводника может быть диэлектрик).

Напряженность электрического поля вблизи поверхности проводника пропорциональна поверхностной плотности заряда  .

Вблизи выпуклых частей тел поле может быть настолько большим, что происходит ионизация окружающего атмосферного воздуха и коронный разряд.