41. Поток вектора напряженности. Теорема Остроградского-Гаусса для электростатического поля в вакууме и ее применение к расчету полей.

Линии однородного электрического поля напряженностью   пронизывают некоторую площадку S, то поток вектора напряженности (раньше мы называли число силовых линий через площадку) будет определяться формулой:

где E_n – произведение вектора   на нормаль   к данной площадке

Полное число силовых линий, проходящих через поверхность S называется потоком вектора напряженности Ф_Е через эту поверхность.

Таким образом, поток вектора   есть скаляр, который в зависимости от величины угла α может быть как положительным, так и отрицательным.

Теорема Остроградского-Гаусса позволяет определить поток вектора напряженности электростатического поля, создаваемого системой зарядов.

теорема Гаусса для электростатического поля в вакууме: поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на ε₀. Эта теорема получена математически для векторного поля произвольной природы русским математиком М.В.Остроградским (1801—1862), а затем независимо от него применительно к электростатическому полю — К. Гауссом. 

Примеры расчетов

Равномерно заряженная бесконечная плоскость

Пусть   — поверхностная плотность заряда на плоскости (41.1).

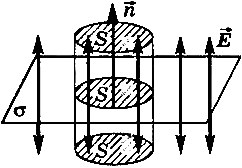
Рис. 41.1

В качестве поверхности площадью S выберем цилиндрическую поверхность, образующая которой перпендикулярна плоскости. Основания этого цилиндра расположены перпендикулярно линиям напряженности по обе стороны от плоскости. Так как образующие цилиндра параллельны линиям напряженности (  = 90°, cos  = 0), то поток через боковую поверхность цилиндра отсутствует, и полный поток через поверхность цилиндра равен сумме потоков через два основания: N = 2ES. Внутри цилиндра заключен заряд q =  S, поэтому, согласно теореме Остроградского-Гаусса,

где   = 1 (для вакуума), откуда следует, что напряженность поля равномерно заряженной бесконечной плоскости

Бесконечная равномерно заряженная нить

Пусть   — линейная плотность заряда нити. Выделим участок нити длиной   и окружим его цилиндрической поверхностью, расположенной так, что ось цилиндра совпадает с нитью (рис. 41.2).

Рис. 41.2

Линии напряженности электростатического поля, создаваемого нитью в сечении, перпендикулярном самой нити, направлены перпендикулярно боковой поверхности цилиндра, поэтому поток напряженности сквозь боковую поверхность  , где R — радиус цилиндра. Через оба основания цилиндра поток напряженности равен нулю (  = 90°, cos  = 0). Тогда полный поток напряженности через выделенный цилиндр

Заряд, находящийся внутри этого цилиндра,  .

Согласно теореме Остроградского—Гаусса, можно записать

Следовательно, модуль напряженности поля, создаваемого равномерно заряженной бесконечно длинной нитью на расстоянии R от нее,

42. Работа электростатического поля по перемещению в нем заряда. Циркуляция вектора напряженности электростатического поля.

При перемещении пробного заряда q в электрическом поле электрические силы совершают работу. Эта работа при малом перемещении   равна

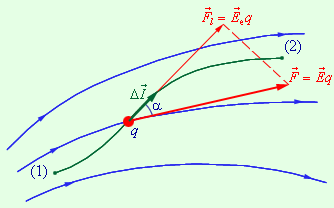
Рис. 42.1

Электростатическое поле обладает важным свойством:

Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.

Аналогичным свойством обладает и гравитационное поле, и в этом нет ничего удивительного, так как гравитационные и кулоновские силы описываются одинаковыми соотношениями.

Следствием независимости работы от формы траектории является следующее утверждение:

Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.

Силовые поля, обладающие этим свойством, называют потенциальными или консервативными.

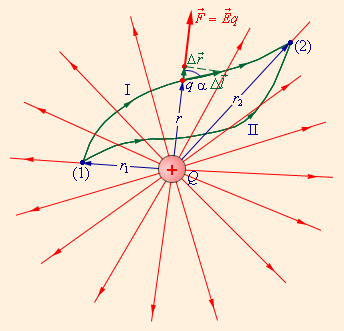
На рис. 42.1 изображены силовые линии кулоновского поля точечного заряда Q и две различные траектории перемещения пробного заряда q из начальной точки (1) в конечную точку (2). На одной из траекторий выделено малое перемещение   Работа ΔA кулоновских сил на этом перемещении равна 

Таким образом, работа на малом перемещении зависит только от расстояния r между зарядами и его изменения Δr. Если это выражение проинтегрировать на интервале от r = r1 до r = r2, то можно получить

Рис. 42.2

Если пробный заряд q совершил малое перемещение   вдоль силовой линии из точки (1) в точку (2), то можно записать: ΔA₁₂ = qEΔl = q(φ₁ – φ₂) = – qΔφ, где Δφ = φ₁ – φ₂ – изменение потенциала.

Циркуляцией вектора напряженности называется работа, которую совершают электрические силы при перемещении единичного положительного заряда по замкнутому пути L

Так как работа сил электростатического поля по замкнутому контуру равна нулю (работа сил потенциального поля), следовательно циркуляция напряженности электростатического поля по замкнутому контуру равна нулю.