25. Основное уравнение молекулярно-кинетической теории идеальных газов.

Простейшей моделью, рассматриваемой молекулярно-кинетической теорией, является модель идеального газа. В кинетической модели идеального газа молекулы рассматриваются как идеально упругие шарики, взаимодействующие между собой и со стенками только во время упругих столкновений. Суммарный объем всех молекул предполагается малым по сравнению с объемом сосуда, в котором находится газ. Модель идеального газа достаточно хорошо описывает поведение реальных газов в широком диапазоне давлений и температур. Задача молекулярно-кинетической теории состоит в том, чтобы установить связь между микроскопическими (масса, скорость, кинетическая энергия молекул) и макроскопическими параметрами (давление, объем, температура).

В результате каждого столкновения между молекулами и молекул со стенками скорости молекул могут изменяться по модулю и по направлению; на интервалах времени между последовательными столкновениями молекулы движутся равномерно и прямолинейно. В модели идеального газа предполагается, что все столкновения происходят по законам упругого удара, т. е. подчиняются законам механики Ньютона.

Используя модель идеального газа, вычислим давление газа на стенку сосуда. В процессе взаимодействия молекулы со стенкой сосуда между ними возникают силы, подчиняющиеся третьему закону Ньютона. 

Формула для среднего давления газа на стенку сосуда запишется в виде

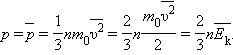
Это уравнение устанавливает связь между давлением p идеального газа, массой молекулы m₀, концентрацией молекул n, средним значением квадрата скорости   и средней кинетической энергией   поступательного движения молекул. Его называют основным уравнением молекулярно-кинетической теории газов.

Таким образом, давление газа равно двум третям средней кинетической энергии поступательного движения молекул, содержащихся в единице объема.

В основное уравнение молекулярно-кинетической теории газов входит произведение концентрации молекул n на среднюю кинетическую энергию   поступательного движения. Если предположить, что газ находится в сосуде неизменного объема V, то   (N – число молекул в сосуде). В этом случае изменение давления Δp пропорционально изменению   средней кинетической энергии.

26. Барометрическая формула. Закон Больцмана для распределения частиц во внешнем потенциальном поле.

Это выражение называется барометрической формулой. Она позволяет найти атмосферное давление в зависимости от высоты или, измерив давление, найти высоту: Так как высоты обозначаются относительно уровня моря, где давление считается нормальным, то выражение может быть записано в виде

– давление на высоте

Выражение называется распределением Больцмана для внешнего потенциального поля. Из него видно, что при постоянной температуре плотность газа больше там, где меньше потенциальная энергия его молекул.

27. Явление переноса. Опытные законы диффузии, теплопроводности и внутреннего трения.

Беспорядочное тепловое движение молекул, непрерывные столкновения между ними приводят к тому что молекулы, хотя и сравнительно медленно, перемещаются из одной точки пространства в другую. В результате столкновения изменяются величины и направления скоростей молекул, что приводит к передаче импульса и энергии. По этой причине в газовой среде, если рассматривать бесконечно малые объемы отдельных участков среды, самопроизвольно возникают флуктуации плотности (концентрации), температуры и давления газа, которые мгновенно исчезают. Если данные неоднородности вызваны посторонним источником и носят постоянный характер, то хаотическое движение молекул стремится ликвидировать эти неоднородности. При этом в газе возникают особые процессы, которые носят название явлений переноса. К ним относятся диффузия, теплопроводность и внутреннее трение.

Если в локальном объеме распределена примесь другого газа (или увеличена плотность данного газа), то хаотическое движение молекул будет способствовать выравниванию концентрации газовых молекул. Процесс выравнивания концентрации газовых молекул называется диффузией. Наблюдения показывают, что в процессе диффузии через площадь поверхности   , расположенную нормально оси, вдоль которой происходит изменение концентрации вещества за время   , переносится масса вещества   , пропорциональная градиенту концентрации   , площади   и времени  .

Это уравнение выражает закон Фика. Величина D называется коэффициентом диффузии. Знак минус означает, что масса переносится в сторону убывания концентрации. С точки зрения молекулярно-кинетической теории

Таким образом, коэффициент диффузии определяется средней длиной свободного пробега   и средней арифметической скоростью   молекул.

В случае неодинаковых температур в различных частях газа те молекулы, которые находятся в более теплых областях, в среднем обладают большей кинетической энергией, чем молекулы в более холодных областях. И здесь молекулярное движение сопровождается суммарным переносом энергии в направлении более холодных частей газа, вследствие чего происходит выравнивание температуры. Этот процесс называется теплопроводностью. Явление теплопроводности заключается в переносе теплоты   от более горячего слоя с температурой   к более холодному, температура которого   , Закон теплопроводности был сформулирован Фурье: теплота   переносимая через элемент площади   за время   , пропорциональна градиенту температуры   , площади   и времени   :

где χ - коэффициент теплопроводности.

Если два соприкасающихся слоя движутся с различными скоростями, то может происходить выравнивание скоростей слоев газов. В среднем импульсы молекул таких слоев различны - молекулы более быстрых слоев имеют большие значения импульсов. Переход молекул из быстрых слоев в более медленный сопровождается переносом импульса упорядоченного движения. Противоположное по характеру действие оказывают молекулы медленного слоя, перешедшие в быстрый слой, - в этом слое возникают тормозящие силы. Суммарный эффект при этом - выравнивание скоростей слоев. Это явление называется внутренним трением. При этом закон, установленный Ньютоном, гласит: сила вязкости F пропорциональна градиенту скорости   и площади S трущихся слоев:

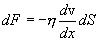
η - коэффициент внутреннего трения (динамическая вязкость). С точки зрения молекулярно-кинетической теории.