
- •Система отсчета. Траектория материальной точки. Скорость, как производная радиус-вектора по времени.
- •Угловая скорость и угловое ускорение, их связь с линейными величинами.
- •Закон инерции. Инерциальная система отсчета. Масса, сила, второй закон Ньютона.
- •Третий закон Ньютона. Механическая система. Внешние и внутренние силы.
- •Импульс материальной точки и системы материальных точек. Закон сохранения импульса.
- •Энергия, как мера различных форм движения и взаимодействия материи. Работа силы и ее выражение через криволинейный интеграл.
- •Кинетическая энергия материальной точки и системы материальных точек и ее связь с работой внешних сил.
- •Поле, как форма материи, осуществляющая силовые взаимодействия. Консервативные и неконсервативные силы.
- •Потенциальная энергия материальной точки во внешнем силовом поле и ее связь с силой. Понятие о градиенте скалярной функции.
- •Закон сохранения механической энергии.
- •Удар абсолютно упругих тел.
- •Удар абсолютно неупругих тел.
- •Момент инерции материальной точки и твердого тела. Теорема Штейнера. Кинетическая энергия вращения.
- •Момент силы. Уравнение динамики вращательного движения твёрдого тела.
- •Момент импульса твердого тела. Закон сохранения момента импульса.
- •Инерциальные системы отсчета. Преобразования Галилея. Механический принцип относительности.
- •Гармонические колебания и их характеристики. Дифференциальное уравнение гармонических колебаний.
- •Пружинный, физический и математический маятники.
- •Энергия гармонических колебаний.
- •Сложение гармонических колебаний с одинаковой амплитудой и близкими частотами (биения).
- •Волны в упругой среде. Поперечные и продольные волны. Уравнение бегущей волны.
- •Образование стоячих волн. Уравнение стоячей волны.
- •Законы идеального газа. Уравнение Клапейрона-Менделеева.
- •Основное уравнение молекулярно-кинетической теории идеальных газов.
- •Барометрическая формула. Закон Больцмана для распределения частиц во внешнем потенциальном поле.
- •Явление переноса. Опытные законы диффузии, теплопроводности и внутреннего трения.
- •Внутренняя энергия системы. Число степеней свободы молекулы. Законы равномерного распределения энергии по степеням свободы молекул.
- •Первое начало термодинамики. Работа газа при изменении его объема.
- •Теплоемкость. Уравнение Майера.
- •Применение первого начала термодинамики к изопроцессам.
- •Адиабатический процесс.
- •Круговой процесс или цикл. Обратимые и необратимые процессы.
- •Тепловые двигатели и холодильные машины. Второе начало термодинамики.
- •Цикл Карно и его кпд для идеального газа.
- •Силы и потенциальная энергия межмолекулярного взаимодействия. Особенности жидкого и твердого состояния.
- •Агрегатное и фазовое состояние вещества. Фазовые переходы I и II рода.
- •Отступление от законов идеального газа. Реальные газы. Уравнение Ван-дер-Ваальса. Изотермы Ван-дер-Ваальса. Внутренняя энергия реального газа.
- •Электрический заряд. Электростатическое поле. Закон Кулона.
- •Напряженность электростатического поля. Силовые линии электростатического поля. Принцип суперпозиции электростатического поля.
- •Поток вектора напряженности. Теорема Остроградского-Гаусса для электростатического поля в вакууме и ее применение к расчету полей.
- •Равномерно заряженная бесконечная плоскость
- •Бесконечная равномерно заряженная нить
- •Работа электростатического поля по перемещению в нем заряда. Циркуляция вектора напряженности электростатического поля.
- •Потенциал электростатического поля.
- •Связь напряженности и потенциала электростатического поля. Эквипотенциальные поверхности.
- •Типы диэлектриков. Поляризация диэлектриков.
- •Поляризация диэлектриков
- •Вектор поляризации. Напряженность поля в диэлектрике.
- •Вектор электрического смещения. Теорема Остроградского-Гаусса для электростатического поля в диэлектриках.
- •Проводники в электростатическом поле. Распределение зарядов в проводниках. Поле внутри проводника и на его поверхности.
- •Напряженность электрического поля внутри проводника должна быть равной нулю:
- •Электроемкость уединенного проводника и конденсатора. Конденсаторы. Электроемкость плоского конденсатора. Соединения конденсаторов.
- •Энергия системы неподвижных точечных зарядов, заряженного проводника, конденсатора. Энергия электростатического поля. Объемная плотность энергии.
Система отсчета. Траектория материальной точки. Скорость, как производная радиус-вектора по времени.
Система отсчета — это тело или совокупность тел, по отношению к которым рассматривается движение других тел. Система отсчета состоит из тела (или тел) отсчета, жестко связанной с ним (с ними) системы координат и системы измерения времени — часов.
Траекторией материальной точки называется линия, описываемая пространстве этой точкой при ее движении.
Вектор
скорости
материальной
точки
в
каждый момент времени определяется как
производная по времени радиус-вектора ![]() текущего
положения этой точки, так что:
текущего
положения этой точки, так что:
![]() .
.
Ускорение. Нормальное и тангенциальное ускорение.
Ускорение – это величина, которая характеризует быстроту изменения скорости.
Например, автомобиль, трогаясь с места, увеличивает скорость движения, то есть движется ускоренно. Вначале его скорость равна нулю. Тронувшись с места, автомобиль постепенно разгоняется до какой-то определённой скорости. Если на его пути загорится красный сигнал светофора, то автомобиль остановится. Но остановится он не сразу, а за какое-то время. То есть скорость его будет уменьшаться вплоть до нуля – автомобиль будет двигаться замедленно, пока совсем не остановится. Однако в физике нет термина «замедление». Если тело движется, замедляя скорость, то это тоже будет ускорение тела, только со знаком минус (как вы помните, скорость – это векторная величина).
Среднее
ускорение> – это
отношение изменения скорости к промежутку
времени, за который это изменении
произошло. Определить среднее ускорение
можно формулой:
![]()
где – вектор ускорения.
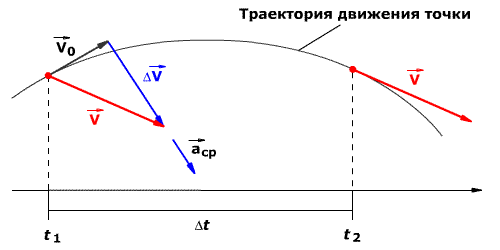
Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
|
Модуль
тангенциального ускорения равен
производной модуля скорости по времени:
Нормальное
ускорение характеризует изменение
скорости по направлению и совпадает
с нормалью к траектории к центру ее
кривизны.
|
Угловая скорость и угловое ускорение, их связь с линейными величинами.
Угловой
скоростью называется
векторная величина, равная первой
производной угла поворота тела по
времени: ![]() .
.
Рис. 1 |
Рис. 2 |
Вектор ω направлен вдоль оси вращения по правилу правого винта, т.е. так же, как и вектор dφ (рис. 2). Размерность угловой скорости dim ω = Т-1, а ее единица — радиан в секунду (рад/с). Линейная скорость точки (см. рис. 1)
|
Угловым
ускорением называется
векторная величина, равная первой
производной yгловой скорости по времени
или второй производной от угла поворота
по времени:
![]()
|
|
При вращении тела вокруг неподвижной оси вектор углового ускорения ε направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор ε сонаправлен вектору ω (рис. 3), при замедленном - противонаправлен ему (рис. 4). |
Связь между линейными и угловыми характеристиками движущейся точки
![]() ,
,
![]() .
.




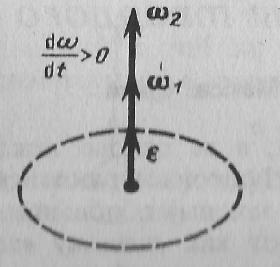 Рис.3
Рис.3 Рис.4
Рис.4