Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный университет им. М.В. Ломоносова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

MB контр.р_Стат_ЕК_ОА.doc

Скачиваний:

Добавлен:

01.05.2025

Размер:

1 Mб

Скачать

☆

1 / 51 2 3 4 5 > Следующая >>>

КРИВОРІЗЬКИЙ ФАКУЛЬТЕТ

ДЕРЖАВНОГО ВИЩОГО НАВЧАЛЬНОГО ЗАКЛАДУ

„ЗАПОРІЗЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ”

МІНІСТЕРСТВА ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ

Салип Ю.О.

Статистика

Методичні вказівки та тематика контрольних робіт

Кривий Ріг

2011

І. Методичні вказівки до виконання контрольної роботи

Для рішення завдання № 1 необхідно вивчити тему «Зведення та групування статистичних даних».

Групування – розчленування, розподіл одиниць сукупності на класи, групи та підгрупи за суттєвими ознаками. Виділяють структурні, типологічні та аналітичні групування.

За допомогою аналітичного групування виявляють взаємозв’язки між двома ознаками, з яких одна представляє результат, а інша - фактор, що впливає на результат.

Аналітичні групування здійснюють за факторною ознакою.

Первинний ряд наглядно не дає уявлення про розподіл одиниць за величиною ознаки в сукупності. Тому першим кроком для упорядкування первинного ряду є його ранжування, тобто розміщення усіх варіант ряду за напрямком зростання чи спаду. Ранжований ряд даних дозволяє виявити мінімальне і максимальне значення ознаки.

Потім визначають ширину інтервалу, яка при заданій кількості груп і рівних інтервалах дорівнює

де х_тах і х_тіп - відповідно максимальне та мінімальне значення ознаки;

т – число груп.

Точність ширини інтервалу повинна визначатись у відповідності до ступеня точності даних спостереження:

якщо дані спостереження подані а точністю до 0,1 то величина інтервалу округляється до цілих із десятими.

Ширина інтервалу дозволяє визначити межі усіх інтервалів ряду розподілу.

В кожен інтервал включають варіанти, числові значення яких більше або рівні нижній межі і менші або рівні верхній межі цього інтервалу.

В кожній групі визначають кількість підприємств, обсяг результативної та факторної ознаки, їх середній рівень.

Рішення задачі повинно бути оформленим у вигляді робочої таблиці (по усій сукупності), таблиці кінцевого ряду розподілу та його гістограми.

При побудові гістограми на осі абсцис відповідно до прийнятого масштабу відкладають нижню і верхню межі інтервалів, а по осі ординат - частоти. Потім для кожного інтервалу будують прямокутник основою якого є відрізок на осі абсцис, а висота якого пропорційна частоті інтервалу.

В кінці рішення задачі здійснюють аналіз результатів і роблять висновки.

За наявністю зв’язку між факторною і результативною ознаками групові середні від групи до групи поступово змінюються – збільшуються чи зменшуються. Це свідчить про наявність зв’язку.

Для розв’язання завдання №2 необхідно вивчити тему: «Аналіз рядів розподілу», «Вибірковий метод. Статистична перевірка гіпотез»:

1) засвоїти методи розрахунків в інтервальному ряді розподілу середніх величин, абсолютних та відносних показників варіації;

2) усвідомити поняття генеральної і вибіркової сукупності, частки вибірки у генеральній сукупності

та вибіркової частки, якій притаманна певна ознака (d);

3) оволодіти методами розрахунків граничної помилки параметрів вибіркової сукупності.

Для визначення середньої та показників варіації ознаки X за даними інтервального ряду складають табл. 1.1.

Таблиця 1.1

Розрахункові данні для рішення задачі № 2.

Групи підприємств за вартістю основних фондів	Кількість підприємств
1	2	3	4	5	6	7
В цілому по сукупності		Х		Х	Х

Перші дві графи таблиці заповнюються за даними інтервального ряду розподілу задачі №1.

Розрахунок середньої за згрупованими даними носить умовний характер, так як ґрунтується на припущенні, що в межах інтервалу індивідуальні значення ознаки розподіляються рівномірно.

Середню визначають за формулою середньої арифметичної зваженої

де - середнє значення ознаки j-ої групи, для кожної групи визначається як середнє значення інтервалу, тобто як півсума двох його меж;

- частота j-ої групи;

= п - число значень ознаки по сукупності в цілому.

Для характеристики варіації ознаки X необхідно обчислити дисперсію, середнє квадратичне відхилення та квадратичний коефіцієнт варіації.

Дисперсія – це середній квадрат відхилень від середньої. Для згрупованих даних

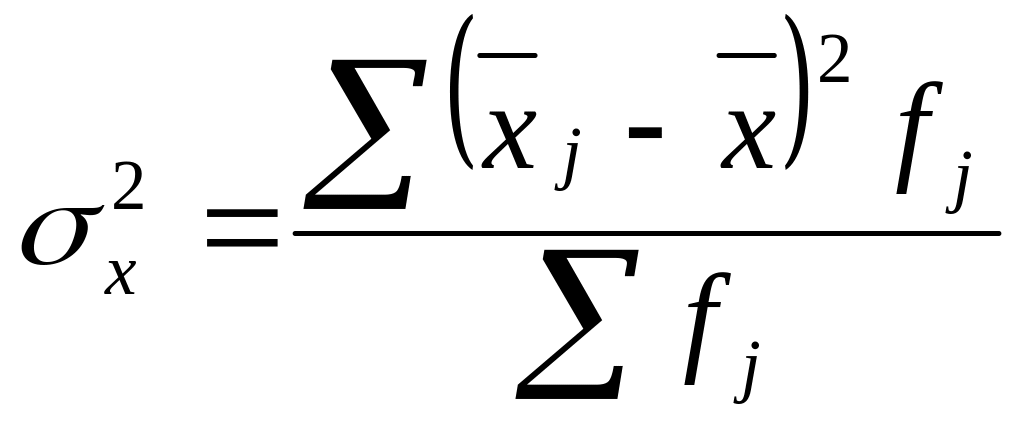Середнє квадратичне відхилення – це корінь квадратний з дисперсії.

Коефіцієнта варіації розраховують як відношення абсолютних характеристик варіації до характеристики центру розподілу. Квадратичний коефіцієнт варіації обчислюють за формулою

Вважають, що сукупність є однорідною, а середня типовою, коли коефіцієнт варіації не перевищує 33%.

Вибіркова сукупність, яка обстежується є частиною генеральної сукупності з якої проводиться відбір ознак для спостереження.

Між характеристиками вибіркової сукупності і характеристиками генеральної сукупності, як правило існують деякі розходження, які називають помилкою вибірки.

Розмір граничної помилки вибірки залежить від варіації ознаки , обсяг вибірки (п) та її частини у генеральній сукупності ймовірності , від прийнятого рівня

де t – квантиль нормального розподілу, довірче число (коефіцієнт довіри), який вказує як співвідносяться гранична і стандартна помилки вибірки для прийнятого рівня ймовірності;

– стандартна помилка вибірки, середнє квадратичне відхилення вибіркових оцінок від значень параметра генеральної сукупності.

В економічних розрахунках рекомендується використовувати довірчу ймовірність 1 – α = 0,95 або 1 – α = 0,954, для яких квантиль t відповідно складає 1,96 та 2,00. (додаток 1)

У теорії вибіркового методу розглядається два способи відбору: повторний і безповторний. При повторному відборі за схемою кулі, що повертається імовірність попасти в вибірку однакова для всіх елементів сукупності. При безповторному відборі за схемою кулі, що не повертається відібрана одиниця не повертається назад і ймовірність відбору окремих елементів весь час змінюється.

Використання випадкової повторної вибірки в практиці обмежено. Тому в задачі визначають середню квадратичну помилку випадкової безповторної вибірки за формулою

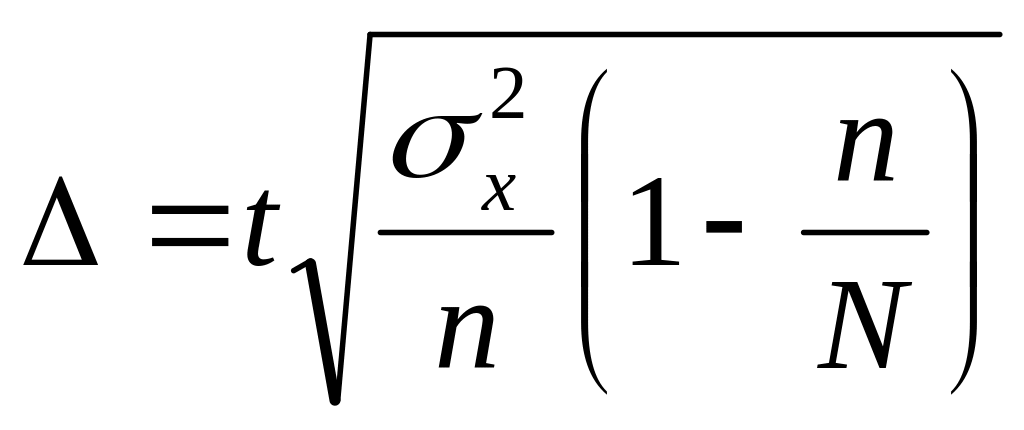де п – обсяг вибірки;

N – обсяг генеральної сукупності.

Довірчі межі генеральної середньої визначаються за формулами

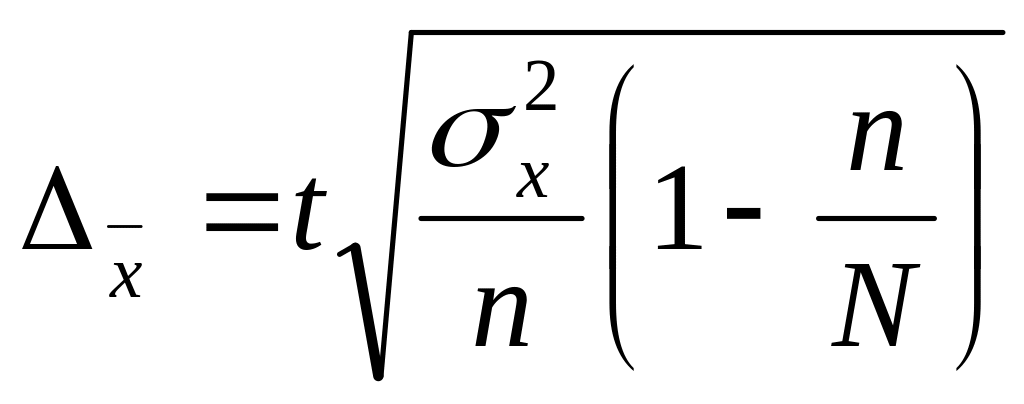де – гранична помилка вибіркової середньої.

Довірчі межі частки Р визначають наступним чином

де Р – генеральна частка;

d – вибіркова частка;

– гранична помилка вибіркової частки.

Мода (М_о) – це найбільш поширене значення ознаки. Моду розраховують за формулою

де х₀ – нижня межа модального інтервалу;

h – ширина модального інтервалу;

– відповідно частоти (частки) модального передмодального і післямодального інтервалів;

Медіана (М_е) – значення ознаки, яке припадає на середину впорядкованого ряду, поділяє його навпіл – на дві рівні за обсягом частини.

Медіану в интервальному ряду знаходять за наступною формулою

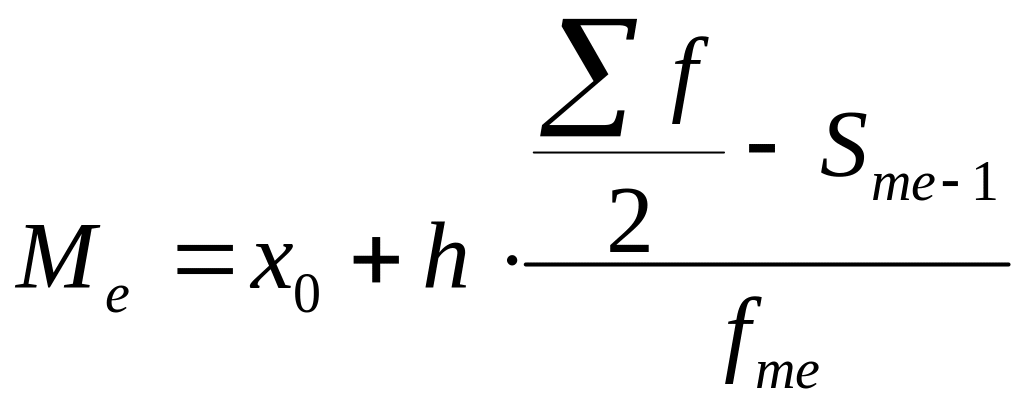де х₀, h – відповідно нижня межа і ширина медіанного інтервалу;

– сума накопичених частот в пердмедіаному інтервалі;

– частота медіаного інтервалу.

В завдання № 3 передусім необхідно розрахувати абсолютні та відносні характеристики ряду динаміки.

Динамічний ряд – це послідовність чисел, які характеризують зміну того чи іншого соціально-економічного явищам Для динамічного ряду характерні перелік хронологічних дат або інтервалів часу і конкретні значення відповідних статистичних показників, які називають рівнями ряду.

Розрахунок характеристик рядів динаміки ґрунтується на зіставленні рівнів ряду

Абсолютний приріст відображає абсолютну швидкість зміни рівнів ряду, розраховується як різниця рівнів динамічного ряду

ланцюгові	базисні

Коефіцієнт зростання розраховується як відношення рівнів ряду

ланцюгові	базисні

Темп приросту показує на скільки процентів рівень більше (менше) рівня, взятого за базу порівняння:

ланцюгові

базисні

Абсолютне значення 1% приросту показує, чого вартий один процент приросту, розраховується як співвідношення абсолютного приросту і темпу приросту

для ланцюгових темпів приросту

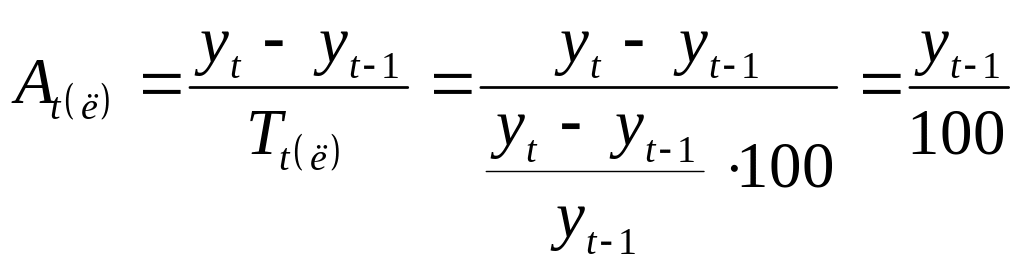для базисних темпів приросту

Середній абсолютний приріст розраховується як середня арифметична проста з ланцюгових абсолютних приростів

Середній коефіцієнт зростання розраховується за формулою середньої геометричної

де п – число ланцюгових коефіцієнтів зростання.

Другим питанням рішення задачі №3 є визначення тенденції зростання обсягу виробництва, продукції за допомогою лінійного тренду.

Тенденція – це основний напрямок розвитку її описують функцією

де t = 0, 1, 2, …, п – зміни часу;

– теоретичні рівні ряду.

При відносно стабільних абсолютних приростах використовують лінійний тренд . Параметр b характеризує середній абсолютний приріст, а параметр а – теоретичне значення рівня при t = 0.

Складають систему нормальних рівнянь

Для розрахунку параметрів трендового рівняння в його довірчих межах та коефіцієнта автокореляції заповнюють табл. 1.2

Таблиця 1.2

Розрахункові дані для розв’язування задачі № 3

Рік	Обсяг вироб-ництва	t	t²
1	2	3	4	5	6	7	8	9	10
1		- 3
2		- 2
3		- 1
4		0
5		1
6		2
7		3
Разом		0				Х		Х

Якщо початок відліку часу (t = 0) перенести в середину ряду, то , а отже

, .

В трендовому рівнянні параметр a – показує середньорічний обсяг виробництва, а параметр b – щорічний абсолютний приріст обсягу виробництва.

Для оцінки автокореляції залишкових величин розраховують коефіцієнт автокореляції за формулою

та порівнюють його з критичним значенням (додаток 5).

За умови, що комплекс причин, які формують тенденцію, ближчим часом не зміниться, можна продовжити тенденцію за межі динамічного ряду і дати точковий прогноз в майбутньому. Для цього необхідно розрахувати теоретичні значення підставивши в трендове рівняння майбутні значення фактору часу.

Інтервальна оцінка прогнозу, тобто його довірчі межі визначаються для ймовірності 1 – α = 0,95 за формулою

де S_р - помилка прогнозу;

t – довірче число для прийнятого рівня імовірності;

V – період упередження.

Помилка прогнозу S_р розраховується за формулою

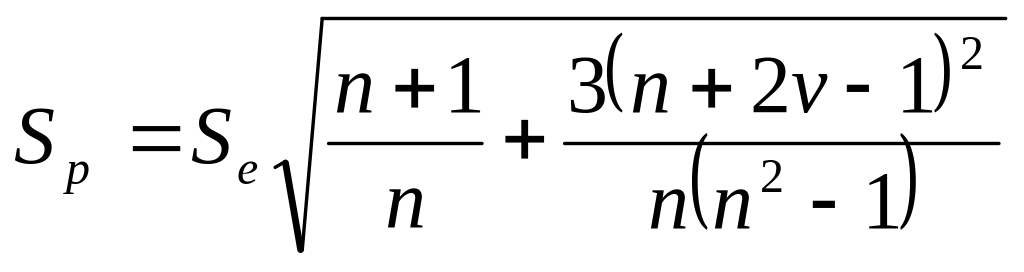де оцінка – оцінка залишкової дисперсії;

т – число параметрів рівняння.

Критичні значення t критерія Стьюдента для імовірності 1 – α = 0,95 та ступенів вільності К = п - т наведенні в додатку 2.

В завдання №4 необхідно перерахувати в умовно-натуральні одиниці кілька разновидів металопродукції, або видів палива за допомогою коефіцієнтів-сумірників. Коефіцієнти перерахунку в умовні одиниці металопродукції наведено в завданні, а для перерахунку обсягу видобутку палива в умовні одиниці розраховують калорійні коефіцієнти відношенням теплотворної спроможності певного палива до теплотворної спроможності 7000 Дж, прийнятої за еталон.

Виходячи з обсягів видобутку палива в умовно-натуральному вираженні визначають динаміку

де у₁, у₀ – відповідно обсяги видобутку палива у звітному і базовому періодах.

Структуру виробництва продукції фактично та за планом і видобутку палива в базовому та плановому періодах визначають також за обсягами в умовно-натуральних одиницях.

Зміна часток окремих складових частин сукупності – це наслідок структурних зрушень. Структурні зрушення оцінюють за допомогою абсолютних і відносних характеристик динаміки.

Абсолютний приріст j-ї частки в процентних пунктах розраховуються за формулою

А коефіцієнти зростання j-ї частки

Як узагальнюючі характеристики інтенсивності структурних зрушень застосовують лінійний і квадратичний коефіцієнти, які обчислюють на основі абсолютних приростів часток

, .

Квадратичний коефіцієнта розрахований на основі коефіцієнтів зростання чутливіше відповідає на зміни в структурі

Результати розрахунків структури виробництва і характеристик структурних зрушень необхідно подати в табл. 1.3.

Таблиця 1.3

Вид продукції	Обсяги виробництва в умовно-натуральному вираженні, млн. т		Структура обсягів виробництва, %		Абсолютні відхилення часток	Коефіцієнти зростання (зменшення) часток,
	за планом	фактично	за планом	фактично
Разом			100	100

Розрахунок квадратичних коефіцієнтів структурних зрушень проводять з використанням даних табл. 1.4.

Таблиця 1.4

Розрахункові дані для визначення квадратичних

коефіцієнтів структурних зрушень

Види продукції	Абсолютне відхилення часток,
Разом	0

Завдання № 5 передбачає закріплення знань з теми «Статистичні методи вимірювання зв’язку». В першій частині задачі №5 за результатами аналітичного групування здійсненого в задачі №1 необхідно охарактеризувати вплив факторної ознаки х на результативну ознаку у, використавши метод аналітичного групування.

Метод аналітичного групування використовують для характеристики лінії регресії кореляційного зв’язку. Лінія регресії – це функція, яка зв’язує середні значення ознаки у із значеннями факторної ознаки х.

Метод аналітичного групування полягає в тому, що всі елементи сукупності групуються за факторною ознакою х і в кожній групі обчислюють середні значення результативної ознаки у і х за первинними вихідними даними задачі №1.

Далі вивчаються кількісні співвідношення між ознаками, їх зміни при переході від кожної групи до наступної

Здійснюють висновки про зміну у із зміною х на одиницю виміру при переході від групи до групи.

Тісноту кореляційного зв’язку характеризують кореляційним відношенням

де - міжгрупова дисперсія;

- загальна дисперсія.

Розрахункові дані для обчислення кореляційного співвідношення в табл. 1.5

Таблиця 1.5

Розрахункові данні для обчислення характеристик

Групи підприємств

Кількість підприємств

…

В цілому по сукупності

…

Між групова дисперсія розраховується за формулою

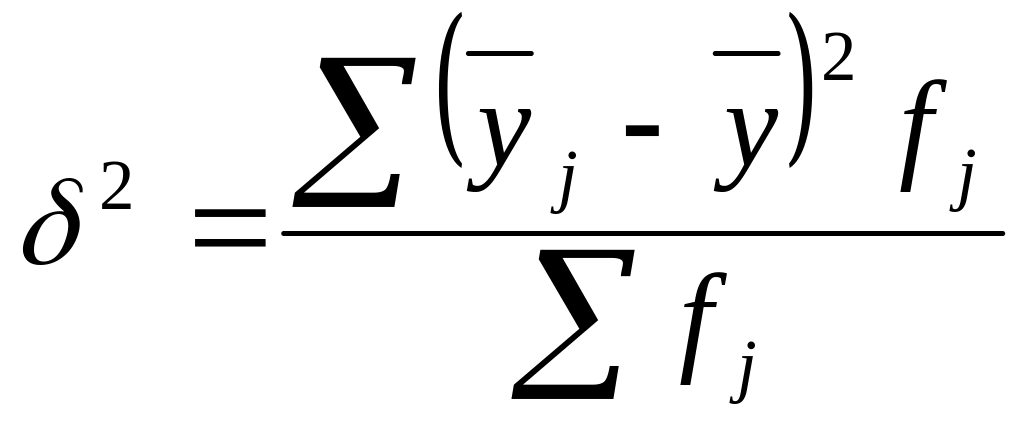Загальна дисперсія

Середній квадрат розраховується за вихідними даними задачі №1.

За статистичною структурою відношення є частиною варіації результативної ознаки у, яка пов’язана з варіацією ознаки х. Перевірка істотності зв’язку між ознаками у і х проводиться за допомогою порівняння фактичних значень або критерій Фішера (F-критерія) з критичними значеннями.

Якщо фактичні значення та F-критерія більше від критичних:

то зв’язок між результативною та факторною ознаками істотний. Критичні значення F і для рівня істотності α = 0,05 наводяться в додатках 3 і 4.

Розподіл та F-критерія в таблицях залежить від числа ступеней міжгрупової (k₁) і середньої з групових (k₂) дисперсій

k₁ = m – 1, k₂ = n – m,

де n, m – відповідно кількість елементів сукупності і груп.

Критерій Фішера обчислюють за формулою:

В другій частині задачі №5 необхідно оцінити лінію регресії за допомогою кореляційно-регресійного аналізу. У моделі регресійного аналізу характеристикою кореляційного зв’язку виступає теоретична лінія регресії, що описується функцією , яка називається рівнянням регресії. Лінійне рівняння регресії має вигляд . Зі змінною х ознаки змінюється більш – менш рівномірно. Для обчислення параметрів рівняння регресії складають систему нормальних рівнянь

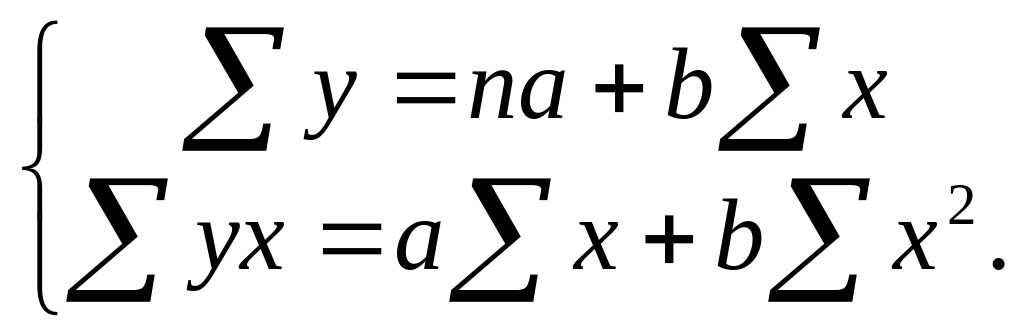
Розрахункові суми для складання системи нормальних рівнянь визначення коефіцієнта детермінації та кореляції послідовно заносять в табл.1.6.

Таблиця 1.6

№ ознаки	х	у	ху	х²	у²	Y
1	2	3	4	5	6	7	8
1 2 . . . 14
Разом						х

Із складеної нормальної системи рівнянь

Параметр b – коефіцієнт регресії, який вказує, на скільки одиниць в середньому змінюється Y із зміною х на одиницю. У випадку прямого зв’язку b – величина додатна, а при зворотному – від’ємна. Параметр а – вільний член рівняння регресії, це значення Y при х = 0.

Мірою тісноти зв’язку в кореляційно-регресійному аналізі виступає коефіцієнт детермінації R², який відображає частку факторної дисперсії у загальній.

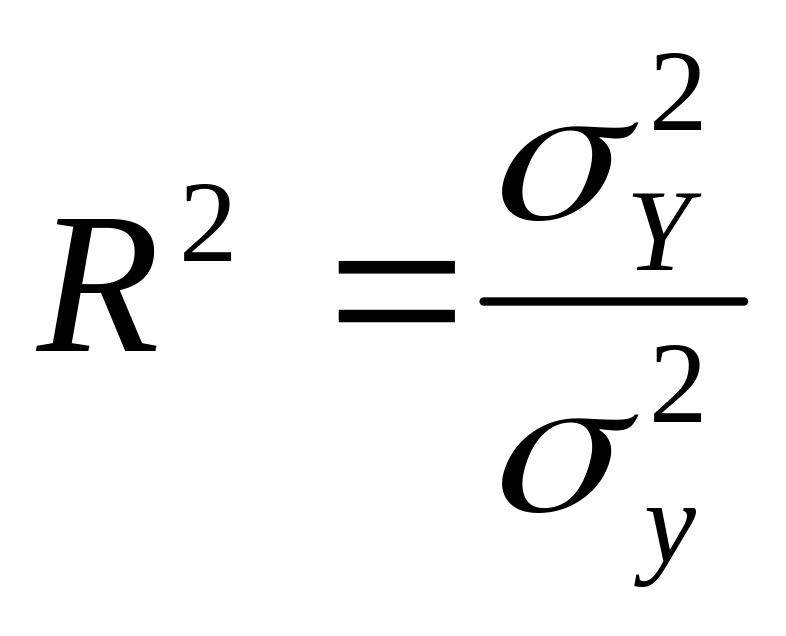Дисперсію теоретичних значень (факторну) визначають за формулою

Загальна дисперсія ознаки дорівнює

Коефіцієнт детермінації R² – характеризує ту частину варіації результативної ознаки у, яка відповідає лінійному рівнянню регресії і змінюється в межах . Індекс кореляції характеризує тісноту зв’язку але економічної інтерпретації не має.

Лінійний коефіцієнт кореляції розраховується за формулою

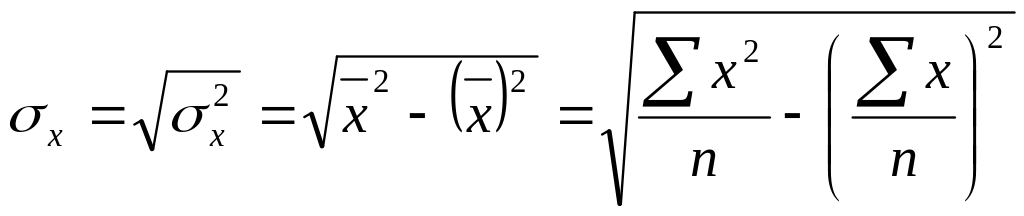Перевірку істотності зв’язку в кореляційно-регресійному аналізі здійснюють за допомогою критичних значень R² та F-критерія. Фактичне значення F-критерія розраховують за формулою.

Ступені вільності залежать від параметрів рівняння (m): k₁ = m – 1, k₂ = n – m. Для лінійної моделі , m = 2.

У невеликих щодо обсягу сукупностях коефіцієнт регресії схильний до випадкових коливань. Тому необхідно визначати довірчі межі коефіцієнта регресії. Стандартна помилка коефіцієнта регресії обчислюється за формулою

Величина граничної помилки

де t – коефіцієнт довіри, визначається для ймовірностей 0,95 , або 0,954 (1,96 і 2,00);

– залишкова дисперсія, яка визначається за формулою.

або .

і характеризує варіацію результативної ознаки у, не пов’язану з варіацією факторної ознаки х. Довірчі межі коефіцієнта регресії складають

Якщо х збільшується на одиницю, рівень у лишається в наведених даних. В кінці рішення задачі прикладається графік кореляційного поля і лінії регресії .

До завдання № 6. Аналіз динаміки економічних показників на основі індивідуальних та агрегатних індексів.

6.1. Вид висхідної інформації

Наприклад: оцінити динаміку показників, що характеризують процес реалізації.