Завдання №4.

Провести ідентифікацію параметрів поліноміальної математичної регресії, яка задана рівнянням параболи другого ступеня вигляду Y=a₀+a₁X+a₂X²що є аналітичним наближенням вибірки експериментальних даних, які наведені в табл.4.1, і оцінити значущість кожного зі знайдених коефіцієнтів, а, також, робото здатність заданої регресійної моделі за критерієм Фішера.

На координатній площині (Х,Y) нанести дані з табл.4.1 і побудувати графік знайденої параболи в діапазоні експериментальних значень Х.

Табл. 4.1

Х	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Y	10	16	20	23	25	26	30	36	48	62	78	94	107	118	127

Розв’язок завдання №4.

В задачі, що нами розглядається, апроксимація дослідних даних відбувається квадратичним поліномом.

. (4.1)

Ідентифікацію статистичного об’єкта, як і в завданні №2, проведемо регресійним методом найменших квадрантів. Критерій мінімума середньоквадратичної похибки в цьому випадку визначається функціоналом

, (4.2)

що повинен задовольняти рівнянням (2.6), які визначають умови знаходження екстремума для (4.2). В явній формі рівняння (2.6) для функціоналу (4.2) мають вигляд:

(4.3)

Після нескладних перетворень в (4.3), отримуємо систему нормальних рівнянь:

(4.4)

Подамо систему (4.4) в матричному вигляді: , де

- квадратна матриця 3х3;

-вектор-стовбець шуканих коефіцієнтів а_і ( і = ) рівняння регресії (4.1);

–вектор-стовбецьвільних коефіцієнтів системи рівнянь (4.4).

Система лінійних рівнянь (4.4) відносно шуканих компонентів вектора може бути розв’язана будь-яким з трьох методів:

• за допомогою правила Крамера;

• методом оберненої матриці;

• методом Гауса (метод виключення невідомих).

Перші два підходи можна застосувати тільки в тих випадках, коли матриця А є не виродженою, тобто коли її визначник – головний визначник Δ системи (4.4) – відмінний від нуля.

Табл. 4.2

1	1	1	1	10	10	10
2	4	8	16	16	32	64
3	9	27	81	20	60	180
4	16	64	256	26	92	368
5	25	125	625	25	125	625
6	36	216	1296	26	156	936
7	49	343	2401	30	210	1470
8	64	512	4096	36	288	2304
9	81	729	6561	48	432	3888
10	100	1000	10000	62	620	6200
11	121	1331	14641	78	858	9438
12	144	1728	20736	94	1128	13536
13	169	2197	28561	107	1391	18083
14	196	2744	38416	118	1652	23128
15	225	3375	50625	127	1905	28575
	1240	14400	178312	820	8959	108805

Матриця А є не виродженою,розв’яжемо рівняння методом оберненої матриці. Застосуємо для вирішення цієї задачі апарат MS Excel.

Отриманий вектор стовбець коефіцієнтів регресії

Підставляючи знайдені значення в (4.1) знаходимо, що регресійна модель експериментальних даних, заданих таблицею 4.1 , має вигляд:

у_м=15,07-1,65х+0,64х². (4.8)

Для перевірки значущості отриманого рівняння регресії визначимо статистику Фішера – F-статистику, – тобто характеристику точності рівняння регресії, що є відношенням частини дисперсії залежної змінної, яка пояснена (обрахована) рівнянням регресії, до непоясненої (залишкової) частини дисперсії цієї ж змінної, яка обумовлена відсутністю інформації про всі точки генеральної сукупності:

, (4.9)

де - об’єм вибірки, - число незалежних параметрів при факторних змінних в рівнянні регресії (в нашому випадку це коефіцієнти при х і х² ) . Залишкова дисперсія - це частина дисперсії залежної змінної у , яка не пояснена рівнянням регресії, її наявність є наслідком дії випадкової складової. У нашому випадку (4.8) т = 2, оскільки х² можна вважати другою незалежною змінною.

Для вибраного рівня значущості α по розподілу Фішера визначається табличне значення , ймовірність перевищення якого у вибірці об’єму п , отриманої з генеральної сукупності без зв’язку між змінними, не перевищує рівня значущості α , і далі порівнюється з фактичним значеннямF – статистики (4.9) для регресійного рівняння (в нашому випадку це (4.8)).

Якщо виконується умова , то встановлений по вибірці функціональний зв'язок між змінними у і х є і в генеральній сукупності , тобто регресійна модель вважається працездатною.

Якщо ж виявляється, що рівняння , то рівняння регресії статистично не значущо, тобто існує реальна ймовірність того, що по вибірці встановлений не існуючий в реальності зв'язок між змінними.

Знайдемо значення F-статистики з (4.9) для нашого випадку, коли n = 15, т = 2; ; при для (4.8). Для цього складемо табл. 4.3.

Табл. 4.3

1	10	14,06	-40,61	-4,06	1649,17	16,48
2	16	14,33	-40,34	1,67	1627,32	2,79
3	20	15,88	-38,79	4,12	1504,66	16,97
4	23	18,71	-35,96	4,29	1293,12	18,40
5	25	22,82	-31,85	2,18	1014,42	4,75
6	26	28,21	-26,46	-2,21	700,13	4,88
7	30	34,88	-19,79	-4,88	391,64	23,81
8	36	42,83	-11,84	-6,83	140,19	46,65
9	48	52,06	-2,61	-4,06	6,81	16,48
10	62	62,57	7,9	-0,57	62,41	0,32
11	78	74,36	19,69	3,64	387,70	13,25
12	94	87,43	32,76	6,57	1073,22	43,16
13	107	101,78	47,11	5,22	2219,35	27,25
14	118	117,41	62,74	0,59	3936,31	0,35
15	127	134,32	79,65	-7,32	6344,12	53,58
	820				22350,57	289,12

За таблицями значень критерію Фішера (Додаток 3) для п = 15, т = 2, α = 0,05 знаходимо, що

(4.10)

Підставляючи значення з табл.4.3 в (4.9), розраховуємо статистику Фішера Fдля нашого випадку:

а це означає, що модель є працездатною.

Взагалі вважається, що для отримання статистично значущих рівнянь регресії необхідно, щоб задовольнялась умова : . В нашому випадку це виконується, оскільки 15 6⋅2=12.

Після того, як виконана перевірка статистичної значущості регресійного рівняння в цілому корисно, особливо для багатовимірних залежностей, здійснити перевірку на статистичну значущість отриманих коефіцієнтів регресії. Ідеологія перевірки така ж, як і при перевірці рівняння в цілому, але як критерій використовується t-критерій Стьюдента. Перевіряється нульова гіпотеза Н₀ : коефіцієнт а_і є незначущим, тобто а_і=0.

Будемо вважати, що модель (4.1) є двомірною, ввівши для цього нову лінійну факторну змінну х₂ = х². Для цього обраховуємо значення критерію Ст’юдента для коефіцієнтів ; розраховуємо за формулами:

; ,… (4.11)

де - статистична дисперсія і-ї факторної ознаки (незалежної змінної); R_i – коефіцієнт множинної кореляції, що виражається через інформаційну матрицю Фішера М: - залишкова дисперсія, що була обрахована вище. Для нашого випадку можна вважати, що . Знайдемо і :

; . (4.12)

Підставляючи (4.12) в (4.11) , знаходимо:

;

; (4.13)

.

Отримані фактичні значення критерію Стьюдента порівнюються з табличними значеннями критичних точок t_{α, n-m-1}, отриманими з розподілу Стьюдента. Якщо виявляється , що , то відповідний коефіцієнт статистично значущий і приймається альтернатива до Н₀ гіпотеза, в протилежному випадку – ні. Для α = 0,05 і п-т-1=12 знаходимо табличне значення критерію Стьюдента:

_. (4.14)

Порівнюючи (4.14) з (4.13), приходимо до висновку, що ( і = ), а отже всі коефіцієнти регресійної моделі статистично значущі і приймається альтернатива до Н₀ гіпотеза.

Як експрес-метод оцінки значущості коефіцієнтів рівняння регресії можна застосовувати наступне правило: якщо фактичне значення критерію Стьюдента більше 3, то такий коефіцієнт, як правило, виявляється статистично значущим.

На рис. 4.1 відображено обраховану квадратичну регресійну модель і початкові емпіричні дані на координатній площині XОY.

ВИСНОВОК.

Для регресійної моделі , що описується квадратичною функціональною залежністю типу y_n= a₀+ a₁x + a₂x², методом найменших квадратів розраховані коефіцієнти профакторних змінних і за допомогою t-критерію СтЬюдента доказана їхня значущість. Для перевірки значущості отриманого рівняння регресії розраховано статистику Фішера – F – статистику для рівняння значущості а = 0,05 і доказана працездатність запропонованої регресійної моделі. На координатній площині XОY побудовані теоретична і емпірична залежності.

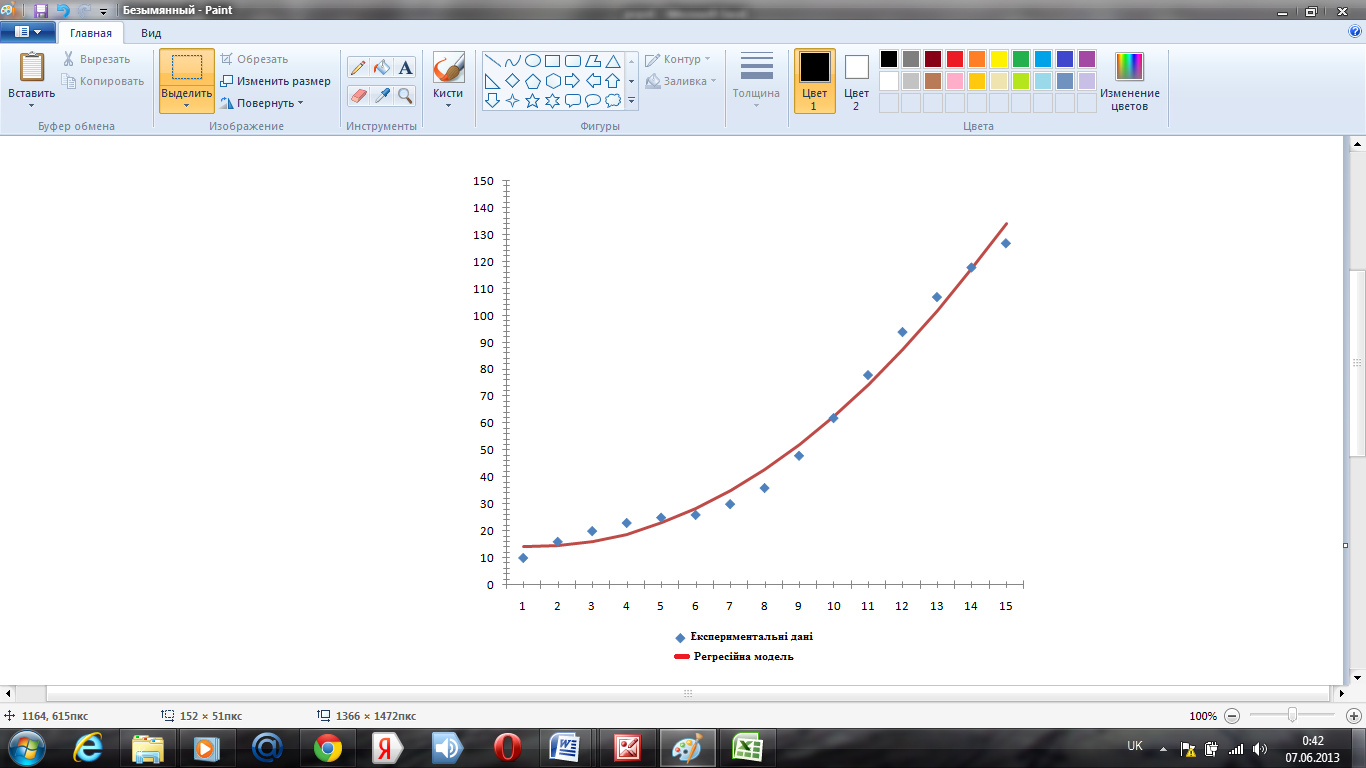
Рис. 4.1. Регресійна модель і емпірична залежність