
Завдання №1.
Дана вибірка експериментальних даних, об’єм якої n становить 200 (табл. 1.1). Результати експерименту згруповані в 10 інтервалів, довжина кожного з них становить 0.2.
Необхідно: перевірити експериментальні дані на відповідність нормальному закону розподілу за допомогою трьох критеріїв згоди:
● спрощеного критерію - методом моментів (через вибіркові значення асиметрії та ексцесу) на основі розрахунку статистичних характеристик;
● критерію Колмогорова;
● критерію Пірсона.
Проміжні результати розрахунків звести до табл. 1 і побудувати гістограму вибірки, а, також, полігон частот.
Табл. 1
x |
ni |
ni xi |
піхі 2 |
пiхi 3 |
пiхi4 |
3,2 |
1 |
|
|
|
|
3,4 |
5 |
|
|
|
|
3,6 |
4 |
|
|
|
|
3,8 |
18 |
|
|
|
|
4,0 |
86 |
|
|
|
|
4,2 |
62 |
|
|
|
|
4,4 |
14 |
|
|
|
|
4,6 |
6 |
|
|
|
|
4,8 |
3 |
|
|
|
|
5,0 |
1 |
|
|
|
|
Сума
|
n=200 |
|
|
|
|
Розв’язок завдання №1
Задача ідентифікації моделей розподілу вибірок часто зустрічається в різних прикладних дослідженнях. Зокрема, більшість параметричних методів статистичного аналізу даних припускають попередню перевірку гіпотези про нормальність закону розподілу досліджуваних даних [1].
Зазначений в таблиці 1.1 експериментальний статистичний матеріал (x1 , x2 … хп) є первинними даними про величину Х, і підлягає статистичній обробці. Зазвичай такі статистичні дані оформляються у вигляді таблиці, гістограми, графіка і тому подібне.
Для того, щоб мати можливість скористатися апаратом теорії ймовірності, доцільно спостережувану величину Х розглядати як неперервну випадкову величину, функцію розподілу якої F(x)=P(X<x) слід визначити. Функція Fn(x)=l/n, де n – об’єм вибірки, а l – число значень Х у вибірці, менших за x, називається емпіричною функцією розподілу. Функція Fn(x) служить оцінкою невідомої функції розподілу F(x).
Перевірка статистичної гіпотези на відповідність експериментальних даних нормальному закону розподілу за спрощеним критерієм – на основі розрахунку коефіцієнтів асиметрії та ексцесу.
Якщо
вибірка об’єму nмістить
з різних елементів x1
, x2
… хп
, причому хi
,
зустрічається пі
разів,
а число пі
називається частотою елементу хі
, а відношення
 ,
називається відносною частотою елементу
хі.
Очевидно, що
,
називається відносною частотою елементу
хі.
Очевидно, що
 ,
a
,
a
 –
об’єм
вибірки, що реалізується.
–
об’єм
вибірки, що реалізується.
Перший стовбець табл. 1.1, який містить в порядку зростання елементи хі , разом з другим стовбцем, що містить їхні частоти пі являють собою варіаційний (статистичний) ряд вибірки.
Нехай
Х
– безперервна випадкова величина з
невідомою густиною ймовірності φ(х).
Для оцінки φ(х)
за вибіркою (xl
, x2
… хп),
що наведена в табл. 1, розіб’ємо область
значень
Х
на k
інтервалів
(груп) довжини hi
i= .
Позначимо через
.
Позначимо через
 i
середини інтервалів, а через ni
– число елементів вибірки, що потрапили
у вказаний інтервал – і-у
групу.
Тоді φ(
i
середини інтервалів, а через ni
– число елементів вибірки, що потрапили
у вказаний інтервал – і-у
групу.
Тоді φ( i)~
i)~
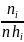 -
оцінка густини ймовірності в точці
i.
В прямокутній системі координат побудуємо
прямокутники з підставами hi
і висотами
,
тобто прямокутники з площами, рівними
відносній частоті і-тої
групи. Отримана таким чином фігура
називається гістограмою вибірки і вона
апроксимує графік невідомої функції
φ(х)
.
З табл. 1.1 видно, що результат експерименту
згрупований в k=10
інтервалів, довжина кожного з них hi
= h
= 0,2.
-
оцінка густини ймовірності в точці
i.
В прямокутній системі координат побудуємо
прямокутники з підставами hi
і висотами
,
тобто прямокутники з площами, рівними
відносній частоті і-тої
групи. Отримана таким чином фігура
називається гістограмою вибірки і вона
апроксимує графік невідомої функції
φ(х)
.
З табл. 1.1 видно, що результат експерименту
згрупований в k=10
інтервалів, довжина кожного з них hi
= h
= 0,2.
Результати проміжних розрахунків зведемо до таблиці 1.2 і побудуємо гістограму вибірки за вихідними експериментальними даними, що наведені в таблиці.
Табл. 1.2
l |
x1 |
n1 |
|
nixl |
nixl2 |
nixl3 |
nixl4 |
1 |
3.2 |
1 |
0,005 |
3,2 |
10,24 |
32,76 |
104,86 |
2 |
3,4 |
5 |
0,025 |
17 |
57,8 |
196,52 |
668,17 |
3 |
3,6 |
4 |
0,02 |
14,4 |
51,84 |
186,62 |
671,85 |
4 |
3,8 |
18 |
0,09 |
68,4 |
259,92 |
987,7 |
3753,25 |
5 |
4,0 |
86 |
0,43 |
344 |
1376 |
5504 |
22016 |
6 |
4,2 |
62 |
0,31 |
260,4 |
1093,68 |
4593,46 |
19292,52 |
7 |
4,4 |
14 |
0,07 |
61,6 |
271,04 |
1192,58 |
5247,33 |
8 |
4,6 |
6 |
0,03 |
27,6 |
126,96 |
584,02 |
2686,47 |
9 |
4,8 |
3 |
0,015 |
14,4 |
69,12 |
331,78 |
1592,53 |
10 |
5,0 |
1 |
0,005 |
5 |
25 |
125 |
625 |
k=10 |
Сума ∑ і |
n=200 |
1 |
816 |
3341,6 |
13734,43 |
56657,96 |
Обрахуємо
статистичні характеристики вибірки
такі, як, вибіркові початкові
 і
центральні
і
центральні
 , моменти порядку v
, що визначаються відповідно формулами:
, моменти порядку v
, що визначаються відповідно формулами:

, (1.1a)

, (1.1b)
При v=1 з (1.1a) ми маємо перший початковий момент

,(1.1c)
що являє собою середнє арифметичне спостережених значень випадкової величини Х, що має назву «вибіркове середнє».
При v=2 з (1.1b) ми маємо другий центральний момент

,(1.1d)
що
являє собою вибіркову дисперсію, а s= – вибіркове
середньоквадратичне відхилення.
– вибіркове
середньоквадратичне відхилення.
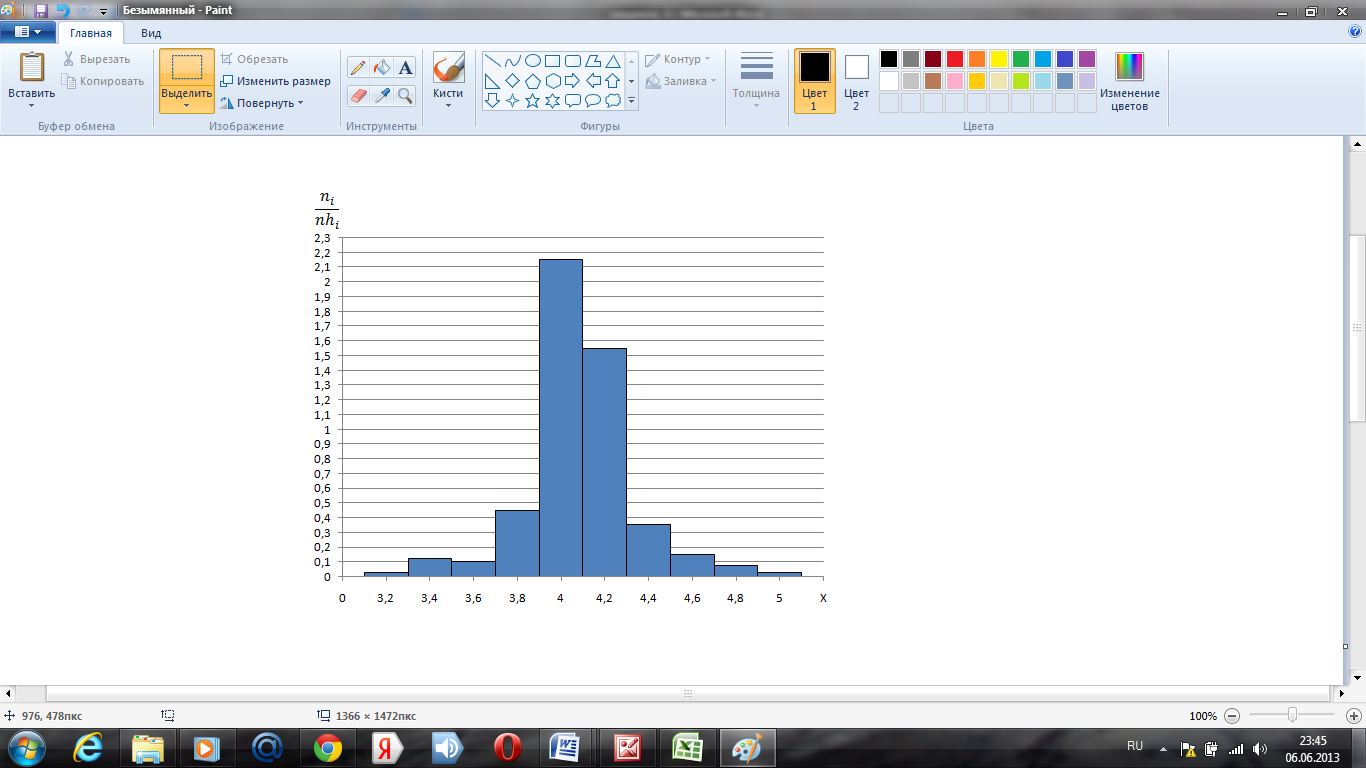
Рис. 1.1. Гістограма вибірки
Моменти і інші характеристики, які ми оцінюємо за нашими вибірковими характеристиками, є характеристиками даного вибіркового групованого розподілу. Але в дійсності нам потрібно знати не характеристики дискретного групованого розподілу Fn(x), а характеристики αv і μv істинного неперервного розподілу F(x).
При
певних умовах наближені значення
моментів αv
і
μv
можна отримати додаючи деякі правки
до моментів
 v
і
v
і
 v
,
що
носять назву поправок Шеппарда [1].
Загальна
формула для поправок Шеппарда має
вигляд:
v
,
що
носять назву поправок Шеппарда [1].
Загальна
формула для поправок Шеппарда має
вигляд:

, (1.2)
де,
 – числа
Бернуллі,
що визначаються з рекурентного
співвідношення
– числа
Бернуллі,
що визначаються з рекурентного
співвідношення
 =1,
=1,

для
m≥2,
де,
 - біномальні коефіцієнти (
- біномальні коефіцієнти ( ).
).
Для перших чотирьох початкових моментів з (1.2) маємо:
α1= 1,
α2=
2
-
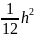 ,
,
α3=
3
-
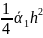 ,
,
α4=
4
–

(1.2a)
(1.2b)
(1.2c)
(1.2d)
Для центральних моментів маємо:

 ,
,
 ,
,
 .
.
(1.3a)
(1.3b)
(1.3c)
(1.3d)
На основі центрального моменту третього порядку можна побудувати показник, що характеризує міру асиметричності розподілу:
 =
= , (1.4)
, (1.4)
σ= - середньоквадратичне відхилення
розподілу.
називають
коефіцієнтом асиметрії, якщо
- середньоквадратичне відхилення
розподілу.
називають
коефіцієнтом асиметрії, якщо
 то
в цьому випадку асиметрія є правостороння
(
то
в цьому випадку асиметрія є правостороння
(
 -
- >0,
де
- мода розподілу, тобто значення ознаки
з найбільшою частотою).
>0,
де
- мода розподілу, тобто значення ознаки
з найбільшою частотою).
При
 асиметрія лівостороння і
-
<0.
Коли
=0,
і тоді
=
.
асиметрія лівостороння і
-
<0.
Коли
=0,
і тоді
=
.
Для характеристики гостровершинності або плосковершинності розподілу служить четвертий центральний момент. Ці властивості розподілу oписуються за допомогою так званого ексцесу. Ексцесом випадкової величини називається величина
 .
(1.5)
.
(1.5)
Число
3 віднімається з відношення
 тому, що для дуже важливого і широко
поширеного в природі нормального закону
розподілу
тому, що для дуже важливого і широко
поширеного в природі нормального закону
розподілу
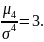 Таким
чином, для нормального розподілу ексцес
дорівнює нулю; криві, більш гостро
вершинні в порівнянні з нормальною,
мають позитивний ексцес; криві більш
плоско вершинні – мають негативний
ексцес.
Таким
чином, для нормального розподілу ексцес
дорівнює нулю; криві, більш гостро
вершинні в порівнянні з нормальною,
мають позитивний ексцес; криві більш
плоско вершинні – мають негативний
ексцес.
За
значенням показників асиметрії і
ексцесу емпіричного розподілу можна
судити про близькість цього розподілу
до нормального, знаючи дисперсії
коефіцієнтів асиметрії
 і ексцесу
і ексцесу
 .
Для цього потрібно оцінити значущість
відмінності |Аs|
і |Ех|
від нуля. Якщо модулі коефіцієнта
асиметрії і ексцесу не перевищують
своїх триразових і п’ятикратних
середньоквадратичних відхилень
.
Для цього потрібно оцінити значущість
відмінності |Аs|
і |Ех|
від нуля. Якщо модулі коефіцієнта
асиметрії і ексцесу не перевищують
своїх триразових і п’ятикратних
середньоквадратичних відхилень
 і
і відповідно,
тобто:
відповідно,
тобто:
|
Аs| ≤3σas, |Ех|≤5σex,
=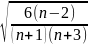 ,
,

(1.6)
(1.6a)
Цей розподіл можна вважати нормальним, а точніше кажучи – не відкидати гіпотезу про схожість фактичного розподілу з нормальним.
Розрахуємо статистичні характеристики, використовуючи проміжні розрахунки з табл.1.2.
Визначимо вибіркове середнє згідно (1.1с):

(1.7a)
Центральний
момент другого порядку
 ,
або вибіркова дисперсія Δ згідно (1.1d):
,
або вибіркова дисперсія Δ згідно (1.1d):
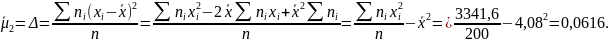
Згідно
(1.3b)
дисперсія
 дорівнює:
дорівнює:

(1.7b)
Згідно
(1.3с) центральний момент третього порядку
 дорівнює:
дорівнює:

Згідно
(1.1b)
центральний момент четвертого порядку
 дорівнює:
дорівнює:

За
(1.3d)
знаходимо
 :
:

(1.8)
Знайдемо
коефіцієнт асиметрії розподілу
 відповідно
до (1.4):
відповідно
до (1.4):

(1.9)
Тобто асиметрія є незначна і правостороння.
Знайдемо величину ексцесу відповідно до (1.5):

(1.10)
 крива
розподілу є більш гостро вершинною в
порівнянні з нормальною кривою.
крива
розподілу є більш гостро вершинною в
порівнянні з нормальною кривою.
З
(1.6а) розраховуємо
і
 :
:

3
(1.11a)

5 =1,669. (1.11b)
Підставляючи
значення
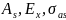 і
з
(1.90) – (1.11) в (1.6) знаходимо, що відмінність
коефіцієнта асиметрії від нуля в рамках
зазначеного критерію незначна, тобто
нерівність для |
і
з
(1.90) – (1.11) в (1.6) знаходимо, що відмінність
коефіцієнта асиметрії від нуля в рамках
зазначеного критерію незначна, тобто
нерівність для | |
,
яка має вигляд
|
|=0,060667
<
0,5118 = 3
,
задовольняється, тоді як відмінність
коефіцієнта ексцесу, а саме |
|
,
яка має вигляд
|
|=0,060667
<
0,5118 = 3
,
задовольняється, тоді як відмінність
коефіцієнта ексцесу, а саме | |
від
нуля значна і задовольняється протилежна
нерівність: |
|
=
2,747465>1,669=
|
від
нуля значна і задовольняється протилежна
нерівність: |
|
=
2,747465>1,669= ,
що свідчить про те, що емпіричний
розподіл не є нормальним.
,
що свідчить про те, що емпіричний
розподіл не є нормальним.
ВИСНОВОК.
Оскільки одна з двох умов значущості статистичних характеристик критерію (1.6) для заданої вибіркової сукупності не виконується, то гіпотезу про схожість заданого емпіричного розподілу з нормальним слід відкинути.
ІІ. Перевірка статистичної гіпотези на відповідність експериментальних даних нормальному закону розподілу за критерієм Колмогорова.
Оскільки усі припущення про характер того або іншого розділу – це гіпотези, то вони мають бути піддані статистичній перевірці за допомогою критеріїв згоди, які дають можливість встановити, коли розбіжності між теоретичними і емпіричними частотами слід визнати несуттєвими, тобто випадковими, а коли – істотними (невипадковими). Таким чином, критерії згоди дозволяють відкинути або підтвердити правильність висуненої гіпотези про характер розподілу в емпіричному ряду.
Звичайна процедура ідентифікації законів розподілу випадкових величин пропускає два основні етапи дослідження – висунення гіпотез про закон розподілу і їх перевірку на основі тих або інших статистичних критеріїв [2, 3]. При цьому формальна постановка задачі на другому етапі може бути різною. У статистиці її зазвичай формулюють як перевірку нульової гіпотези про те, що наявні дані відповідають деякому повністю визначеному закону розподілу або розподілу, що належить деякому параметрично заданому сімейству, параметри якого необхідно оцінити в процесі ідентифікації (проста і складна гіпотези) [4]. Для вирішення цього завдання за наявними емпіричними даними обчислюють значення відповідного критерію і порівнюють його з критичною величиною для заданого рівня значущості. При цьому можливі помилки прийняття неправильної нульової гіпотези або відхилення правильної. Розробляючи критерії, ці помилки прагнуть мінімізувати, але зробити їх рівними нулю принципово не можливо. До того ж зниження вірогідності однієї з помилок веде до збільшення ймовірності іншої.
Критерій
Колмогорова-Смірнова дозволяє оцінити
істотність відмінностей між двома
емпіричними вибірками, а критерій
Колмогорова – порівнювати емпіричний
розподіл з теоретичним. Необхідна умова
застосування критерію Колмогорова-Смірнова
– це щоб об’єми вибірок порівнюваних
розподілів були досить великими:
 ,
,
 .
.
Критерій Колмогорова дозволяє знайти точку, в якій модуль різниці відносних частот двох розподілів – теоретичного і емпіричного- є найбільшим, і оцінити достовірність цієї розбіжності. За нульову гіпотезу Н0 приймається твердження: «Відмінності між двома розподілами несуттєві, судячи по точці максимальної розбіжності відповідних відносних частот».
Алгоритм застосування критерію Колмогорова виглядає таким чином:
Записуються варіаційні ряди емпіричної і контрольної (теоретичної) вибірок.
Обчислюються відносні частоти
 і
і
 для двох наявних вибірок.
для двох наявних вибірок.Записуються модулі різниць d1=|
 |
і шукається найбільший dmax.
|
і шукається найбільший dmax.Визначається емпіричне значення критерію λемп за допомогою формули λемп=dmax⋅
 . (1.12)
. (1.12)Визначається критичне значення критерію
 для заданого рівня значущості α , яке
порівнюється з λемп>
,
то Н0
відхиляється на заданому рівні
значущості α.
для заданого рівня значущості α , яке
порівнюється з λемп>
,
то Н0
відхиляється на заданому рівні
значущості α.
Рівень значущості а – це ймовірність того, що помилково буде відхилена висунута гіпотеза Н0. В статистиці користуються трьома рівнями а:
α = 0,1 (в 10 випадках зі 100 може бути відхилена правильна гіпотеза);
α = 0,05 (в 5 випадках зі 100 може бути відхилена правильна гіпотеза);
α = 0,01 (в 1 випадку зі 100 може бути відхилена правильна гіпотеза).
Для
перевірки розподілу на предмет
відповідності нормальному закону
розподілу обчислюють середнє значення
 і середньоквадратичне відхилення σ, а
потім обчислюють відності теоретичні
частоти
і середньоквадратичне відхилення σ, а
потім обчислюють відності теоретичні
частоти
 за наступною формулою:
за наступною формулою:
 (1.13)
(1.13)
 – абсолютна
теоретична частота,
– абсолютна
теоретична частота, ; –крок
(ширина інтервалу даних ознаки,
згрупованих в і-у
групу з серединою в точці
; –крок
(ширина інтервалу даних ознаки,
згрупованих в і-у
групу з серединою в точці
 ),
),
 ,
φ(u)
=
,
φ(u)
=
 .
.
Обчислимо
значення контрольних величин
= на підставі (1.13) і внесемо результати
обчислень в розрахункову табл.1.3.
Значення для
і σ беремо з (1.7a)
– (1.7b):
на підставі (1.13) і внесемо результати
обчислень в розрахункову табл.1.3.
Значення для
і σ беремо з (1.7a)
– (1.7b):
 ;
σ=0,2482; hi=
h=
0,2;
=
0,8058
;
σ=0,2482; hi=
h=
0,2;
=
0,8058
 .
.
Табл. 1.3
i |
xi |
ui |
φi |
fi теор |
fi емп |
| fi теор - fi емп | |
1 |
3,2 |
-3,5455 |
0,000743 |
0,000599 |
0,005 |
0,004401 |
2 |
3,4 |
-2,7397 |
0,009354 |
0,007537 |
0,025 |
0,017463 |
3 |
3,6 |
-1,9339 |
0,061487 |
0,049546 |
0,02 |
0,029546 |
4 |
3,8 |
-1,1281 |
0,211138 |
0,170135 |
0,09 |
0,080135 |
5 |
4,0 |
-0,3223 |
0,378751 |
0,305198 |
0,43 |
0,124802 |
6 |
4,2 |
0,4835 |
0,354934 |
0,286006 |
0,31 |
0,023994 |
7 |
4,4 |
1,2893 |
0,173759 |
0,140015 |
0,07 |
0,070015 |
8 |
4,6 |
2,0951 |
0,044438 |
0,035808 |
0,03 |
0,005808 |
9 |
4,8 |
2,9009 |
0,005937 |
0,004784 |
0,015 |
0,010216 |
10 |
5,0 |
3,7067 |
0,000414 |
0,000334 |
0,005 |
0,004666 |
З табл. 1.3 видно, що dmax= 0,124802 при і = 5. Оскільки п = 200, то згідно (1.12)
λемп=0,124802⋅ = 1,764967. (1.14)
= 1,764967. (1.14)
Перевагою критерію Колмогорова є те, що для вибірок об’ємом n> 35 критичні значення можна визначити не по таблицях, а розрахувати по асимптотичній формулі [5]:
 (1.15)
(1.15)
, де α – рівень значущості.
Для α = 0,1; 0,05; 0,01 з (1.15) маємо відповідно:
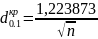 ;
; ;
;
 ;
(1.15a)
;
(1.15a)
,а , отже, порівнюючи (1.15) з (1.15а), знаходимо
 ;
;
 ;
;
 ;
(1.15b)
;
(1.15b)
Порівнюючи значення λемп з (1.14) зі значеннями з (1.15b) бачимо, що задовольняється нерівність
λемп> (1.16)
для кожного з заданих рівнів значущості а . Це означає , що гіпотеза Н0 про несуттєвість відмінностей між теоретичним (нормальним) і емпіричним розподілами відхиляється.
ВИСНОВОК.
Оскільки задовольняється нерівність (1.16) для заданої вибіркової сукупності, то гіпотезу про схожість заданого емпіричного розподілу з нормальним слід відкинути.
ІІІ.
Перевірка статистичної гіпотези на
відповідність експериментальних даних
нормальному закону розподілу за
критерієм згоди Пірсона (критерій
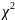 ).
).
Критерій хі-квадрат запропонований в 1900 р. К. Пірсоном. Для його використання проводять попереднє угрупування даних по інтервалах рівної ширини.
Значення критерію розраховують [1] за формулою:

,
де
- спостережувана абсолютна частота
і-тої
групи;
 - теоретична частота попадання даних
в і-й інтервал для вибраного розподілу;
n
– об’єм
вибірки, k
– число груп, на які розбито розподіл.
- теоретична частота попадання даних
в і-й інтервал для вибраного розподілу;
n
– об’єм
вибірки, k
– число груп, на які розбито розподіл.
Для розподілу складені таблиці, де вказано критичне значення критерію згоди для вибраного рівня значущості α і ступенів свободи v . Число ступенів свободи vвизначається як число груп в емпіричному ряді розподілу мінус число зв’язків. Число ступенів свободи v=k – r – 1, де r– число параметрів моделі розподілу, що використовуються для розрахунку теоретичних частот. Зокрема, при розрахунку параметрів моделі за інтервальним варіаційним рядом число ступенів свободи v беруть рівним k – 2 для біноміального і k – 3 – для нормального розподілу, оскільки в останньому випадку використовуються r = 2 параметри : і σ.
Алгоритм застосування критерію виглядає наступним чином.
Записують частоти
 по k
інтервалам.
по k
інтервалам.Перевіряють рівність

Обчислюють значення
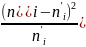
Знаходять
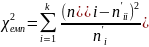
Знаходять
 по
таблиці критичних точок розподілу
по
таблиці критичних точок розподілу

Якщо
 , то приймається гіпотеза Н0
.
, то приймається гіпотеза Н0
.
Розраховуємо
значення
,
 ,
і підставляємо їх в табл.1.4. Значення
розраховуємо за допомогою (1.13) і значень
з табл. 1.3.
,
і підставляємо їх в табл.1.4. Значення
розраховуємо за допомогою (1.13) і значень
з табл. 1.3.
За таблицею критичних точок розподілу [1] по рівнях значущості α = 0,01; 0,05; 0,1 і числу ступенів свободи v = k – 3 = 10 – 3 = 7 знаходимо відповідні критичні точки (див. Додаток 1):
 .
.
Порівнюючи
ці значення зі значенням
 з табл. 1.4 бачимо, що задовольняється
нерівність
з табл. 1.4 бачимо, що задовольняється
нерівність
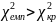 , а це означає, що приймається альтернатива
до Н0
гіпотеза про несхожість заданого
емпіричного розподілу з нормальним.
, а це означає, що приймається альтернатива
до Н0
гіпотеза про несхожість заданого
емпіричного розподілу з нормальним.
Табл. 1.4
i |
xi |
ui |
φi |
|
ni |
(ni- )2 |
|
1 |
3,2 |
-3,5455 |
0,000743 |
0,1198 |
1 |
0,774752 |
6,467045 |
2 |
3,4 |
-2,7397 |
0,009354 |
1,5074 |
5 |
12,198255 |
8,092248 |
3 |
3,6 |
-1,9339 |
0,061487 |
9,9092 |
4 |
34,918645 |
3,523861 |
4 |
3,8 |
-1,1281 |
0,211138 |
34,027 |
18 |
256,86473 |
7,548850 |
5 |
4,0 |
-0,3223 |
0,378751 |
61,0396 |
86 |
623,02157 |
10,891757 |
6 |
4,2 |
0,4835 |
0,354934 |
57,2012 |
62 |
23,028481 |
0,402587 |
7 |
4,4 |
1,2893 |
0,173759 |
28,003 |
14 |
196,08401 |
7,002250 |
8 |
4,6 |
2,0951 |
0,044438 |
7,1616 |
6 |
1,349315 |
0,188410 |
9 |
4,8 |
2,9009 |
0,005937 |
0,9568 |
3 |
4,174666 |
4,363154 |
10 |
5,0 |
3,7067 |
0,000414 |
0,0828 |
1 |
0,841256 |
10,160097 |
|
|
|
|
200,0084 |
200 |
|
|
ВИСНОВОК.
Оскільки не задовольняється нерівність для заданої вибіркової сукупності, то гіпотезу про схожість заданого емпіричного розподілу з нормальним слід відкинути.
Завдання №2
Визначити коефіцієнти зв'язку k1, xp вхідного X та вихідного Y сигналів фазово-часового дискримінатора, що є складовою системи автоматичного супроводу цілі по дальності, якщо відомо, що дискримінаційна характеристика пристрою апроксимується фінітною функцією y(x) кусково-лінійнійного типу:

де
 -
значення розугодження керуючого
сигналу, при якому вихідна напруга
дискримінатора Y=0.
Ідентифікацію
параметрів лінійної математичної
моделі статистичного об’єкта провести:
-
значення розугодження керуючого
сигналу, при якому вихідна напруга
дискримінатора Y=0.
Ідентифікацію
параметрів лінійної математичної
моделі статистичного об’єкта провести:
а) регресійним методом найменших квадратів;
б) з використанням центрованих даних.
Обраховану функціональну залежність зобразити на координатній площині (х,у).
Вихідні експериментальні дані:
Х= {1; 2; 3; 4; 5}; Y={1.25; 2.5; 2.75; 3.5; 4.25}.
Розв’язок завдання №2.
Вихідними даними для розв’язку задачі ідентифікації є кінцеві множини експериментальних значень вхідних (факторних) величин Х об’єкта і відповідних значень вихідних величин Y.
а) Математична модель функціонального зв’язку між вхідними і вихідними змінними задається у вигляді рівняння регресії
 ,
,
яке
в нашому випадку має вигляд (2.2). При
регресійних методах ідентифікації в
якості
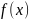 найбільш часто застосовуються степеневі
поліноми:
найбільш часто застосовуються степеневі
поліноми:
 . (2.4)
. (2.4)
Задача
ідентифікації ставиться як знаходження
таких оцінок невідомих параметрів аі
,
 при яких задана рівнянням (2.4) аналітична
залежність буде найкращим чином
апроксимувати експериментальні дані.
при яких задана рівнянням (2.4) аналітична
залежність буде найкращим чином
апроксимувати експериментальні дані.
В якості критерію близькості використовується мінімум квадратичної нев’язки J значень фактичних змінних уі і модельних уMі , що розраховані за рівнянням регресії (2.4):
 (2.5)
(2.5)
де
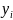 - експериментальне значення вихідної
змінної,
- експериментальне значення вихідної
змінної,
 - відповідне модельне (розрахункове)
значення.
- відповідне модельне (розрахункове)
значення.
Для
обрахунку коефіцієнтів регресії
складають рівняння на знаходження
екстремума по кожному параметру
 :
:
 (2.6)
(2.6)
Сукупність співвідношень (2.5) утворює систему з т+1 рівняння відносно оцінок коефіцієнтів рівняння регресії (2.4), розв’язок якої визначає шукані коефіцієнти.
В нашому випадку, коли рівняння регресії має вигляд (2.2), критерій мінімуму середньоквадратичної похибки визначається функціоналом:

(2.7)
З (2.7) відповідно до (2.6) отримуємо систему нормальних рівнянь:
 (2.8)
(2.8)
Для визначення коефіцієнтів системи (2.8) складаємо таблицю 2.1:
Табл. 2.1
|
|
|
|
1 |
1,25 |
1 |
1,25 |
2 |
2,5 |
4 |
5 |
3 |
2,75 |
9 |
8,25 |
4 |
3,5 |
16 |
14 |
5 |
4,25 |
25 |
21,25 |
|
|
|
|
звідки:
 (2.9)
(2.9)
Розв’язуючи систему (2.9), знаходимо параметри моделі. З першого рівняння системи знаходимо
 (2.10)
(2.10)
Підставляючи
вираз (2.10) для
 в друге рівняння системи (2.9), маємо
рівняння для знаходження
:
в друге рівняння системи (2.9), маємо
рівняння для знаходження
:
15 (2,85 – 3 ) + 55 = 49,75 (2.11)
З (2.11) знаходимо :
10 = 7, або = 0,7. (2.12)
Отже, наша лінійна регресійна модель має вигляд:
 .
(2.13)
.
(2.13)
б) Центрованою називається випадкова величина х , математичне очікування якої M[x] дорівнює нулю. Випадкові величини центрують, віднімаючи від них математичне очікування або його незміщену оцінку.
Якщо
в заданих статистичних спостереженнях
нема систематичної похибки (змішення,
тренду), то в цьому випадку задовольняється
рівність
 , де
і
, де
і
 - вибіркові середні, а
-
коефіцієнт регресії.
- вибіркові середні, а
-
коефіцієнт регресії.
Оцінка коефіцієнта регресії рівняння лінійної регресії знаходиться за формулами:
 (2.14)
(2.14)
де
,( –
коефіцієнт
кореляції).
–
коефіцієнт
кореляції).
 .
(2.15)
.
(2.15)
Розрахуємо модель з використанням центрованих даних. Для цього обчислимо коефіцієнт кореляції між XiYчерез коваріацію цих двох вибірок, що є мірою їхньої лінійної залежності:
 ,
(2.16)
,
(2.16)
де
 - вибіркові дисперсії вибірок X
i
Yвідповідно
– див. (1.1d).
- вибіркові дисперсії вибірок X
i
Yвідповідно
– див. (1.1d).
Обраховуємо
середні вибіркові


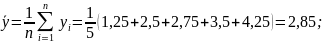
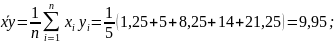

Підставляючи знайдені значення статистичних характеристик в (2.14) знаходимо :
 (2.17)
(2.17)
а
з (2.15) з врахуванням (2.17) знаходимо, що
 ,
що співпадає з (2.13).
,
що співпадає з (2.13).
Обрахована лінійна регресійна модель і початкові емпіричні дані зображені на рис. 2.1.

Рис. 2.1. Регресійна модель і емпірична залежність



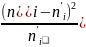

 =58,64
=58,64





