44. Нормальные напряжения в поперечных сечениях стержней (балок) при изгибе

Нормальное напряжение при деформации прямого плоского изгиба в любой точке поперечного сечения произвольной формы:

,

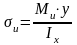где M_и – внутренний изгибающий момент в расчетном сечении стержня (балки);

y – координата точки сечения, т.е. расстояние от нейтральной линии (оси х) сечения до точки, в которой определяется напряжений σ_и;

I_x – момент инерции расчетного сечения стержня относительно оси х.

Максимальное нормальное напряжение при деформации прямого плоского изгиба имеет место в наиболее удаленных от оси х точках сечения (при y_max):

,

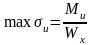где W_x= I_x/y_max – момент сопротивления расчетных точек сечения (единицы измерения W_х – в м³, см³, мм³ и т.п.).

45. Касательные напряжения в поперечных сечениях стержней (балок) при изгибе

Касательное напряжение при деформации прямого плоского изгиба определяется по общей формуле Журавского:

,

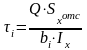где Q – внутренняя поперечная сила в расчетном сечении стержня;

b_i – ширина расчетного сечения на уровне координаты y_i точки i, для которой определяется касательное напряжение τ_i;

S_x^отс – статический момент относительно оси х части площади сечения, отсеченной за пределами координаты y_i расчетной точки i.

Для некоторых форм поперечного сечения значения максимального касательного напряжения max τ в точках, расположенных на нейтральной линии (оси х) можно определять по упрощенным формулам:

- для прямоугольного сечения площадью А = b∙h (где b – ширина и h высота сечения)

,

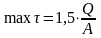- для круглого сплошного сечения площадью А = π∙d²/4 (где d – диаметр сечения)- .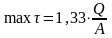

46. Основное условие статической прочности изгибаемых стержней

Основное условие статической прочности, используемое для проверочных расчетов прямых стержней (балок) при прямом плоском изгибе:

,

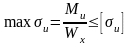где 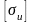– допускаемое нормальное напряжение при изгибе для материала, из которого изготовлен изгибаемый стержень (балка).

Для стальных элементов конструкций можно принимать ≈ 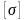, где – основное допускаемое напряжения для материала (при растяжении).

Условие статической прочности, используемое для проектировочных расчетов прямых стержней (балок) при прямом плоском изгибе, при которых определяются требуемые значения характеристик и размеров расчетного сечения:

.

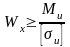По расчетному значению W_x в справочнике подбирают размер стандартного сечения (например, типоразмер стандартного прокатного двутавра) или определяют размер сечения заданной формы. Так, учитывая, что у круглого сплошного сечения W_x=π∙d³/32, то требуемый диаметр такого сечения определится по формуле

.

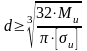Требуемый наружный диаметр d трубчатого сечения при соотношении c = d₀/d (где d₀ – внутренний диаметр трубы) определится по формуле

.

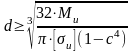Дополнительные проверочные условия статической прочности изгибаемых стержней

Проверочный расчет на статическую прочность по касательным напряжениям при прямом плоском изгибе осуществляется по условию

,

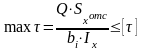где 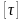– допускаемое касательное напряжение при изгибе для материала, из которого изготовлен стержень (балка).

Для стальных элементов конструкций можно принимать 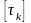= (0,5÷0,6) , где – основное допускаемое напряжение для материала (при растяжении).

В ряде точек расчетного сечения изгибаемого стержня, в которых нормальные и касательные напряжения достигают значительных величин, проводится проверка прочности по эквивалентным напряжениям, в частности, для стальных элементов конструкций – по 4-й теории прочности:

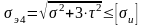или R

Методика подбора размеров поперечных сечений для балок

Размеры сечения балки должны выбираться такими , чтобы ни в одной точке балки напряжения не превосходили допускаемой величины. Выше мы видели, что в балке возникают нормальные и касательные напряжения. 

Размеры сечения балки подбирают по опорному моменту, так как он больше пролетного ; площадь сечения арматуры над каждой опорой получается в 2 раза больше, чем в пролете, что в конструктивном отношении, особенно при армировании плоскими сварными каркасами, очень неудобно.

Размеры сечения балки указаны на фигуре. 

Размеры сечений балки можно выбрать с таким расчетом, чтобы напряжения о во всех сечениях были постоянны. При этом условии мы получим балку равного сопротивления изгибу. 

Таким образом, размеры сечения балки удовлетворяют условиям прочности как по нормальным, так и по касательным напряжениям.