42.Изгибаемые стержни (балки): общая схема деформирования, расчетные схемы, классификация.

Общие положения об изгибаемых стержнях (балках), сущность деформации плоского изгиба.

Деформации изгиба в стержневых элементах инженерных конструкций происходят, как правило, при действии на них внешних поперечных нагрузок. При этом первоначально прямой стержень (до нагружения) после приложения внешних поперечных нагрузок искривляется, в результате чего продольные «волокна» материала, расположенные по разные стороны от продольной центральной оси стержня, получают продольные деформации разного знака – растяжения и сжатия. Если все внешние нагрузки и главные центральные оси инерции всех поперечных сечений стержня располагаются в одной плоскости, то такой изгиб называется плоским прямым изгибом, который и рассматривается в этой лекции.

Иногда изгиб стержня происходит без поперечных сил (когда, например, на стержень действуют только внешние изгибающие моменты): такой изгиб называется чистым изгибом и в сечениях стержня возникают внутренние изгибающие моменты М_и. Более распространен поперечный изгиб, когда в поперечных сечениях стержня возникают внутренние поперечные силы Q и внутренние изгибающие моменты М_и.Внутренние поперечные силы Q и внутренние изгибающие моменты М_и определяются методом сечений.

Классификация балок

Балками называют элементы строительных конструкций, работающие на изгиб. Они могут классифицироваться по разным признакам.

По составу сечения бывают цельные (рис. 7.2, а), выполненные из одного профиля и составные, выполненные из нескольких элементов – профилей или листов. Прокатные балочные двутавры выпускаются по ГОСТ 26020-83 высотой до 1 м, их следует применять, если они есть в наличии. Но возможности их применения ограничены по несущей способности и деформациям. При необходимости приходится применять составные сечения.

Составные сечения в настоящее время выполняются сварными из трех листов в связи с отсутствием ослабления сечения и возможностью применения автоматической сварки на заводах по производству стальных конструкций. В прошлом широко применялись составные стальные балки из листовой стали с поясными уголками на заклепках. При этом количество листов в каждом поясе доходило до трех. В настоящее время вместо заклепок применяют болты.

Болты в составных балках (включая высокопрочные) применяются при укрупнительной сборке, если невозможна сварка.

По статической схеме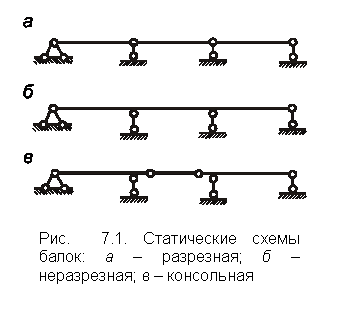 

Разрезные – наиболее металлоемкие, так как в них велики моменты и прогибы при прочих равных условиях, но они просты в монтаже и нечувствительны к неравномерной осадке опор.

Неразрезные – наименее металлоемкие, так как в них прогибы малы и иногда могут быть моменты меньше, чем в разрезных, но они трудоемки в монтаже и требуют надежных оснований.

Консольные – конструкции усложнены из-за пролетных шарниров. Занимают промежуточное положение по показателям между двумя предыдущими схемами.

При малых пролетах и нагрузках, когда экономия на стоимости материала невелика, обычно применяют разрезные балки. При больших пролетах и нагрузках, если можно обеспечить надежные основания, могут быть выгодны неразрезные балки. При невозможности обеспечить надежные основания следует применять разрезные балки.

По форме сечения.

Показателем эффективности сечения балки может быть относительное ядровое расстояние, характеризующее несущую способность по моменту при одинаковой площади и высоте сечения,для прямоугольного сечения оно составляет

 

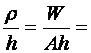
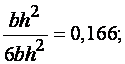
для круглого сечения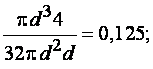   

для кольцевого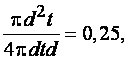 

для прокатных двутавров около 0,33, для составных еще выше.

Поэтому в изгибаемых элементах чаще всего применяются двутавровые сечения, реже коробчатые [7] и швеллеры.

Представленные расчетные схемы позволяют рассчитать балку практически при любом возможном виде нагрузки. Если на балку действует несколько различных нагрузок, то можно производить отдельный расчет для каждой схемы загружения, а затем полученные результаты сложить (с учетом знаков). Это правило называется принципом суперпозиции и в некоторых случаях значительно упрощает общий расчет, а также экономит уйму времени на поиск в сети подходящей расчетной схемы.

43.Внутренние усилия в поперечных сечениях балок, правила знаков, построение эпюр.

Если мысленно рассечь деформированный брус плоским перечным сечением на две части и привести внутренние силы, действующие со стороны одной части на другую - к центру тяжести (площади) поперечного сечения, получим ГЛАВНЫЙ ВЕКТОР R и ГЛАВНЫЙ МОМЕНТ M системы этих внутренних сил. Эти величины (R и M) имеют такой смысл: Если мысленно заменить внутренние силы, действующие в сечении, силой R и моментом (парой сил) M (приложив их в центре тяжести поперечного сечения), то равновесие отсеченной части тела не нарушится. То есть R и M (совместно) являются статическим эквивалентом системы внутренних сил, действующих в сечении. Внутренние усилия возникают во всех точках поперечного сечения балки и распределены по неизвестному закону. Не имея возможности определить эти внутренние усилия для каждой точки сечения, заменяем их статически эквивалентными внутренними силовыми факторами, приложенными в центре тяжести поперечного сечения.

Внутренние силовые факторы определяются из условия равновесиярассматриваемой части балки. Однако можем внутренние силовые факторы найти и непосредственно, как действие отброшенной левой части на правую часть. Видно, что часть балки, нагруженная силой P, стремится изогнуть рассматриваемую нами правую часть выпуклостью вниз, а также пытается произвести срез. Следовательно, в сечении должны возникнуть поперечная сила  и изгибающий момент  .

Осуществим параллельный перенос силы P в центр тяжести поперечного сечения балки. По правилам теоретической механики мы должны добавить момент, равный (рис. 7.1, б).

При прямом изгибе в поперечном сечении балки возникают два внутренних силовых фактора:

изгибающий момент, численно равный алгебраической сумме моментов всех сил, приложенных к отбрасываемой части балки, относительно главной центральной оси, проходящей через центр тяжести рассматриваемого сечения (в рассмотренном нами случае изгибающий момент равен:  );

поперечная сила, численно равная алгебраической сумме всех внешних сил (активных и реактивных), действующих на отбрасываемую часть балки (в нашем случае поперечная сила равна:  ).

Поперечный изгиб - изгиб, при котором в поперечном сечении балки возникают и изгибающий момент, и поперечная сила. Если поперечная сила не возникает, изгиб называется чистым изгибом.