1.Конъюнкция, дизъюнкция және терістеу функцияларын іске асыратын логикалық элементтер (лэ). Ақиқат кестелері, жазылу түрлері.
Логикалық көбейту амалын коньюнкция д.а. логикалық ЖӘНЕ элементі – бірнеше кірісті 1 шығысты болады.
f
(x1x2)=x1*x2
X1 |
X2 |
f |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
Л
X1 |
X2 |
f |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
огикалық қосу амалын дизьюнкция деп атайды, НЕМЕСЕ элементі
f(x1x2)=x1vx2
Терістеу амалы инверсия орындайды, логикалық «емес» элементі
x |
f |
0 |
1 |
1 |
0 |
2. Шеффер штрихі, Пирс жебесі функцияларын іске асыратын логикалық элементтер (лэ). Ақиқат кестелері, жазылу түрлері.
Көбейту ж/е терістеу амалын орындайтын, логикалық ЖӘНЕ-ЕМЕС элементтері Шеффер штрихы д.а.
X1 |
X2 |
y |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
Қосу
ж/е терістеу амалын орындайтын, логикалық
НЕМЕСЕ-ЕМЕС элементін Пирс жебесі д.а.
X1 |
X2 |
y |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
3. Және, немесе, емес логикалық элементтердің схемалық жиналуы және олардың негізгі параметрлері.
ЖӘНЕ-ЕМЕС элементі (Шеффер эл-ті)
НЕМЕСЕ-ЕМЕС элементі (Пирс эл-ті)
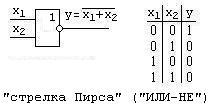
ЖӘНЕ-НЕМЕС-ЕМЕС
Негізгі параметрлері: кіріс б/ша бірігу коэф-ті-логикалық айнымалыларды беруге арналған кіріс санын анықтайды; жүктемелік қабілеті-аналогты элемнттер санын анықтайды; тез әрекеттілігі-ең маңызды параметрлердің бірі, ол сигналды таратудағы кідіріспен бағаланады; кедергіге тұрақтылығы-элементтің жұмыс істеуіне бөгет болмайтын кедергінің максимал мәнімен анықталады.
4. Модулі 2 бойынша қосындылауыш және жартылай қосындылауыш. Шартты графикалық белгіленуі, ақиқат кестесі, кез-келген базистегі схемасы.
Модуль 2 бойынша қосу(XOR)
у=х1
х2
х1 |
х2 |
у |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
Жартылай қосындылауыш - екі кірісі және екі шығысы бар логикалық схема (екі разрядты сумматор, бинарлы сумматор). Жартылай қосындылауыш екілік қосындылауышты тұрғызу үшін қолданылады. Ол А+В суммасын есептеуге мүмкіндік береді, мұндағы А мен В – екілік санның разряды, осыдан нәтиже S және C екі бит болады, мұндағы S-модуль 2 б/ша сумманың биты, ал С – орын ауыстыру биты.
x0=A |
1 |
0 |
1 |
0 |
|
x1=B |
1 |
1 |
0 |
0 |
Функция аталуы |
|
|
|
|
|
|
S |
0 |
1 |
1 |
0 |
Модуль 2 б/ша қосу биты |
C |
1 |
0 |
0 |
0 |
Орын ауыстыру биты |
5. Толық қосындылауыш. Шартты графикалық бейнеленуі, ақиқат кестесі, кез-келген базистегі схемасы. Көпразрядты екілік сандарды қосудың мысалы.
Толық қосындылауыштың схемасы Толық қосындыл-ң шартты белгіленуі
Екілік сандарды қосуды жүзеге асыратын құрылғы – қосындылауыш деп аталады. Екі көпразрядты санды қосқанда, әрбір разряд алдыңғы разрядтан бірді алуы мүмкін немесе келесі разрядқа бірді береді. Осыны ескере отырып екі санның аттас зарядтарынан тұратын толық қосынд-ң ақиқат кестесін жазайық; Мұндағы Аi және Bi – А және В сандарының біраттас разрядтарындағы цифрлар; Pi-1 – i-1 разрядынан i-разрядына өтуші; Si – қосындылардың нәтижесі; Pi – i-разрядтан келесі разрядқа өтуші.
Ақиқат кестесі.
Pi-1 |
Ai |
Bi |
Si |
Pi |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
6. Шифратор. Шартты графикалық белгіленуі, жұмыс істеу қағидасы. 8421-екілік код түрінде ондық сандарды шифрлеу мысалы. Шифратор – ондық сандарды екілік кодқа айналдырады. Олар цифрлық жүйелердегі құрылғыларда мәлімет енгізу үшін қолданылады. nақ.кір=2n шыг
С |
х |
У1 |
У2 |
У3 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
|
2 |
0 |
1 |
0 |
|
3 |
0 |
1 |
1 |
|
4 |
1 |
0 |
0 |
|
5 |
1 |
0 |
1 |
|
6 |
1 |
1 |
0 |
|
7 |
1 |
1 |
1 |
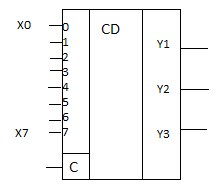
С-стробтаушы (басқарушы кіріс). Шифратордың іске қосылуы басқарушы С кірісіне т/ді, яғни, С кірісіндегі активті сигналдың болу-болмауына т/ді.
7. Дещифраторлар. Шартты графикалық белгіленуі. Екі кірісті тура (тіке) және терістейтін (инверстейтін) шығыстары болатын дешифратордың синтезделу мысалдары.Екілік сандарды ондық сандарға айналдыруда дешифраторлар қолданылады. Кірісі екілік сандар, шығысы ондық сандар үшін арналған. Көбіне цифрлық құрылғыларда қағазға басып шығаруда пайдаланылады.Кіріс саны – n,шығысы – 2n .
Екі кірісті дешифратор
С |
X1 |
X2 |
F |
0 |
0 |
0 |
F0 |
0 |
1 |
F1 |
|
1 |
0 |
F2 |
|
1 |
1 |
F3 |
8-сұрақ. Логика алгебрасының негізгі заңдары мен қатыстары.
Цифрлық құрылғылардың схемаларын құру барысындаоларды суреттеуші логикалық функцияларды әртүрлі мақсатқа сай(мысалы оларды қарапайым түрге келтіру үшін) түрлендіру қажет болды. Бұндай түрлендірімдер логика алгебрасының заңдары мен осы заңдардың жеке жағдайларға тікелей пайдалануға ыңғайландырып шығарылған заңдылықтарының негізінде жүргізіледі.
Коммутативтік немесе алмастырылым заңы
Х1νХ2=Х1νХ2 Х1Х2=Х1Х2
Ассоциативтік немесе біріктірілім заңы
Х3ν(Х2νХ1)=(Х3νХ2) νХ1 Х3(Х2νХ1)=(Х3Х1)Х1
Дистрибутивтік немесе таратылым заңы
Х3Х2νХ2Х1=Х2(Х3νХ1) (Х3νХ2)(Х2νХ1)=Х2ν(Х3Х1)
Де-Морган заны
х1 ν х2=х1 * х2; х1*х2=х1 ν х2
Қарапайым амалдар:
Хν0=Х Хν1=1 ХνХ=Х Хν̅Х=1 Х1νХ1Х0=Х1
Х1ν̅Х1Х0=Х1νХ0 Х^0=0 Х^1=Х Х^Х=Х
Х^̅Х=0 Х1(Х1 νХ0)=Х1 Х1(̅Х1 ν̅Х0)=Х1Х0
Бұл заңдар мен заңдылықтар-симметриялы, яғни олардың дизъюнкциялық және конъюнкциялық түрлері болады.Бұл заңдарың кейбірі дәстүрлі алгебрада қалыптасқан заңдар, сондықтан олардың дұрыстығы күмән тудырмайды,ал дәстүрлі алгебраға тән емес, жаңа заңдар мен заңдылықтардың дұрыстығына көз жеткізу аргументтерінің орындарына олардың сәйкесті мәндерін (0 мен1)қойып тексеру арқылы жүзеге асырылады.