Лекция 1 (03.09)

Предметом теории вероятностей является изучение закономерностей однородных массовых случайных явлений.

Краткая история:

Появление - 17 век, Франция, Паскаль и Ферма формулируют понятия вероятности и математической статистики

18. век, Бернулли доказывает частный случай закона больших чисел (теорема Бернулли)

19. век, Чебышев и его ученики Марков и Ляпунов

20. век, советские ученые Бернштейн и Колмогоров дают логическое обоснование теории вероятностей.

В 17 веке Паскаль назвал теорию вероятностей "математика случая".

Классическое определение вероятности

Случайные события обозначаются латинскими буквами. Вероятностью события A называется отношение числа исходов, благоприятствующих появлению события A, к числу всех равновозможных исходов, образующих полную группу.

A - случайное событие

P - обозначение вероятности

P(A) - вероятность события

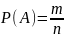
m - число благоприятных исходов

n - число всех возможных исходов

Пример:

В урне находятся 10 шаров. Из них 4 красных и 6 синих. Найти вероятность того, что на удачу шар окажется синим.

Решение:

A = "шар синего цвета"

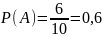
Классификация событий

1. Невозможные события - событие называется невозможным, если оно никогда не произойдет при определённых условиях; P(Н) = 0

2. Достоверные события - событие называется достоверным, если оно обязательно произойдет при определённых условиях; P(Д) = 1

3. Случайные события - событие называется случайным, если оно может произойти или не произойти при определённых условиях; 0 < P(С) <1:

   1. Несовместные - если появление одного из событий исключает появления другого (подбрасываем монету один раз, выпадение орла и решки несовместны, одновременно невозможны)

   2. Совместные - если появление одного из двух событий не исключает появление другого (два раза стреляем по мишени, если мы первый раз попали, то мы можем второй раз и попасть, и промахнутся):

      • Независимые - если появление одного из двух совместных событий не изменяет шансы появления другого (два раза подбрасываем монетку, вероятность выпадения орла или решки независимы)

      • Зависимые - если появление одного из двух совместных событий изменяет вероятность появления другого (имеется в корзине 3 белых и 4 черных шара. Наугад достаём один шар. Потом достаем второй. Узнать вероятность того, что второй шар - чёрный

P(B|A) = 4/6 = 2/3 (если первый - белый) P(B|A) = 3/6 = 1/2 (если первый - чёрный)

Операции над случайными числами

1. Операция сложения

Суммой двух случайных событий A и B называется такое случайное событие A + B, при котором произойдёт событие A, событие B или оба вместе (два выстрела: попали либо при первом выстреле, при втором или при обоих) Сумма нескольких случайных событий означает такое случайное событие, при котором выполнится хотя бы одно из них. (Какое-то n-ное событие, или 2 и 3 или первое и последнее)

2. Операция произведения

Произведением двух случайных событий A и B называется такое случайное событие A + B, при котором одновременно произойдут событие A и событие B.