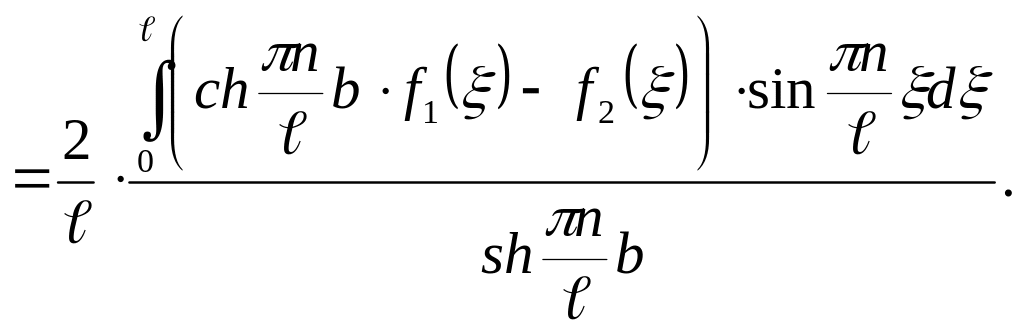4.3. Sadə oblastlarda sərhəd məsələlərinin həllinə Furye üsulunun tətbiqi

Bir sıra sadə oblastlar üçün sərhəd məsələləri dəyişənlərə ayırma üsulu ilə həll oluna bilər.

Məsələ 4.1. Radiusu olan dairə üçün daxili Dirixle mə­sə­ləsini həll etməli.

Həlli. Məsələdə

(4.32)

, (sərhəd şərti) (4.33)

, (həllin periodikliyi şərti) (4.34)

(həllin məhdudluğu şərti) (4.35)

şərtlərini ödəyən funksiyasını tapmaq tələb olunur. Burada oblast dairə olduğundan, başlanğıc olaraq, dairənin mər­kəzi qəbul edilməklə polyar koordinat sistemindən istifadə edilmişdir.

Məsələni dəyişənlərə ayırma (Furye) üsulu ilə həll etmək üçün (4.32) tənliyinin xüsusi həllini

, (4.36)

şəklində axtaraq. Həllin fərz etdiyimiz (4.36) şəklini (4.32) tənliyində yerinə yazıb, dəyişənləri ayırsaq,

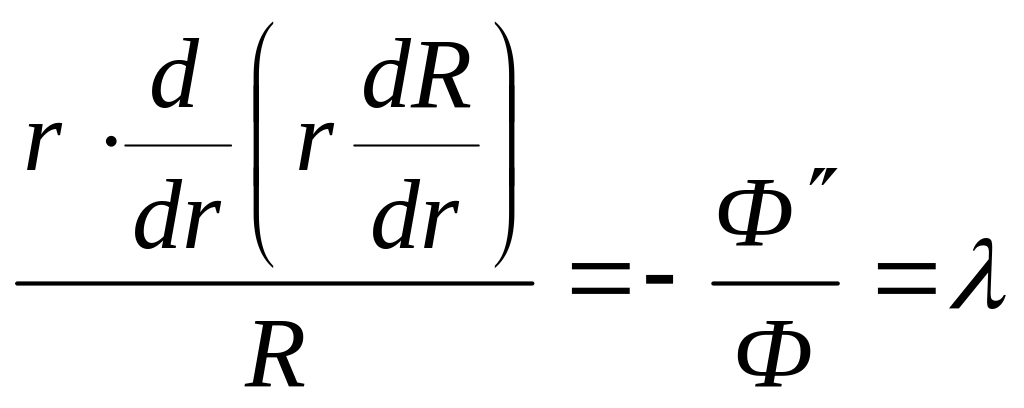
alarıq, burada . Buradan iki tənlik alınır:

, (4.37)

. (4.38)

(4.34) şərtindən

,

(4.39)

olar, yəni funksiyası bucağının dövrlü dövri funksiyasıdır.

olduqda (4.37) tənliyinin (4.39) şərtini ödəyən həlli yoxdur. Deməli və bu halda (4.37) tənliyinin ümumi həlli

(4.40)

şəklində olar. (4.40) funksiyasının (4.39) şərtini ödəməsi üçün

olmalıdır. Buradan

Beləliklə, (4.37), (4.39) məsələsinin məxsusi ədədləri

(4.41)

onlara uyğun məxsusi funksiyaları isə

olar. Qeyd edək ki, olduqda (4.37) tənliyinin ümumi həlli

yalnız olduqda (4.39) şərtini ödəyir. Deməli, məxsusi ədədinə mxsusi funksiyası uyğundur.

Beləliklə, (4.37) funksiyasının (4.39) şərtini ödəyən həlləri

(4.42)

şəklində alınır.

(4.48) tənliyinin həllini

şəklində axtaraq, burada naməlum ədəddir.

Bu funksiyanı (4.48) tənliyində yerinə yazsaq və -yə ixtisar etsək,

və ya

alarıq. Deməli,

, (4.43)

burada C və D-sabitlərdir. (4.43) funksiyası olduqda sonsuzluğa çevrilir və dairə daxilində bu funksiyanın (4.45) şərtini ödəməsi üçün , yəni

götürmək lazımdır.

Beləliklə, (4.32) tənliyinin (4.34), (4.35) şərtlərini ödəyən (4.36) şəklində olan xüsusi həllərini tapmış oluruq:

.

(4.32) – (4.35) məsələsinin həllini bu xüsusi həllərin cəmi şəklində yazmaq olar:

. (4.44)

və əmsallarını tapmaq üçün (4.33) şərtindən istifadə edək:

. (4.45)

funksiyasını Furye sırasına ayıraq:

, (4.46)

burada

(4.46)-nı (4.45)-də yerinə yazsaq və sıraları müqayisə etsək,

alarıq. Beləliklə, dairə daxili üçün Dirixle məsələsinin həllini

(4.47)

sırası şəklində alırıq.

Eyni qayda ilə dairə xarici üçün Dirixle məsələsini həll etsək,

(4.48)

alarıq.

Qeyd. Xarici məsələdə (4.43) bərabərliyində qəbul etmək lazımdır.

Məsələ 4.2. Düzbucaqlı oblastda Dirixle məsələsini həll etməli.

Həlli. Məsələdə düzbucaqlı ob­las­tın­da Laplas tənliyi üçün birinci sərhəd məsələsini həll et­mək tələb olunur, yəni

, (4.49)

, (4.50)

(4.51)

şərtlərini ödəyən və oblastında kəsilməz olan funksi­yası­nı tapmaq tələb olunur.

(4.49) tənliyinin (4.51) bircins şərtlərini ödəyən həllini

, (4.52)

şəklində axtarırıq.

(4.52)-ni (4.49)-da yerinə yazaraq, alınan tənliyi dəyi­şənlə­ri­nə ayırsaq,

alarıq. Buradan

, (4.53)

. (4.54)

(4.51) sərhəd şərtlərindən alırıq ki,

. (4.55)

(4.53), (4.55) məsələsinin olduqda yalnız trivial həlli vardır. Deməli, və bu halda (4.53) tənliyinin ümu­mi həlli

şəklində olar. (4.55) şərtlərindən istifadə etsək,

məxsusi ədədlərini alarıq. Bu məxsusi ədədlərə uyğun məxsusi funksiyalar

(4.56)

olar.

İndi isə (4.54) tənliyini həll edək.

olduğunu nəzərə alsaq,

tənliyinin ümumi həlli

olar. Deməli, (4.49) tənliyinin yalnız (4.51) şərtlərini ödəyən xüsusi həlləri

(4.57)

funksiyaları olar.

Beləliklə, (4.49) – (4.51) məsələsinin həllini

sırası şəklində yazmaq olar.

və əmsallarını təyin etmək üçün (4.50) sərhəd şərt­lərindən istifadə edək:

,

.

Buradan

və

.