2.2. Birölçülü dalğa tənliyi üçün Koşi məsələsinin və yarımoxda sadə sərhəd məsələlərinin həlli

Hiperbolik tipli tənliklərə gətirilən məsələlərin həllinin qu­rul­ması üsullarının öyrənilməsini qeyri-məhdud (sonsuz) sim üçün Koşi məsələsinin həllindən başlayacağıq.

Məsələ 2.3. Sonsuz simin nöqtələrinin başlanğıc vəziy­yə­ti və sürəti məlum olduqda onun rəqslərinin qanununu ifadə edən funksiyanı tapmalı.

Həlli. Göstərmişdik ki, müəyyən şərtlər daxilində simin rəqs­lərini u(x,t) funksiyası ilə ifadə etmək olar və bu funk­siyanın tapılması aşağıdakı Koşi məsələsinin həllinə gətirilir:

(2.23)

(2.24)

(2.25)

burada və simin nöqtələrinin uyğun olaraq başlan­ğıc vəziyyətini və sürətini xarakterizə edən verilmiş funksiya­lar­dır. Fərz edək ki, -in ikinci tərtib, -in isə birinci tərtib kəsilməz törəməsi vardır ( ).

(2.23) tənliyinin ümumi həllini tapmaq üçün onu qarışıq törəmə iştirak edən kanonik şəklə gətirək.

Göstərmişdik ki (Misal 1.4),

dəyişənlərini qəbul edərək, (2.23) tənliyini

(2.26)

şəklinə gətirmək olar. (2.26) tənliyini -yə görə inteqrallasaq,

,

-dan asılı ixtiyari funksiyadır, sonuncu tənliyi isə -ya görə inteqrallasaq,

alarıq, burada yalnız -dən asılı ixtiyari funksiyadır,

.

Beləliklə, (2.26) tənliyinin ümumi həlli

(2.27)

şəklində yazılır, burada və öz arqumentlərinin II tərtibdən kəsilməz törəmələri olan ixtiyari funksiyalarıdır. Məsələn, asanlıqla yoxlamaq olar ki,

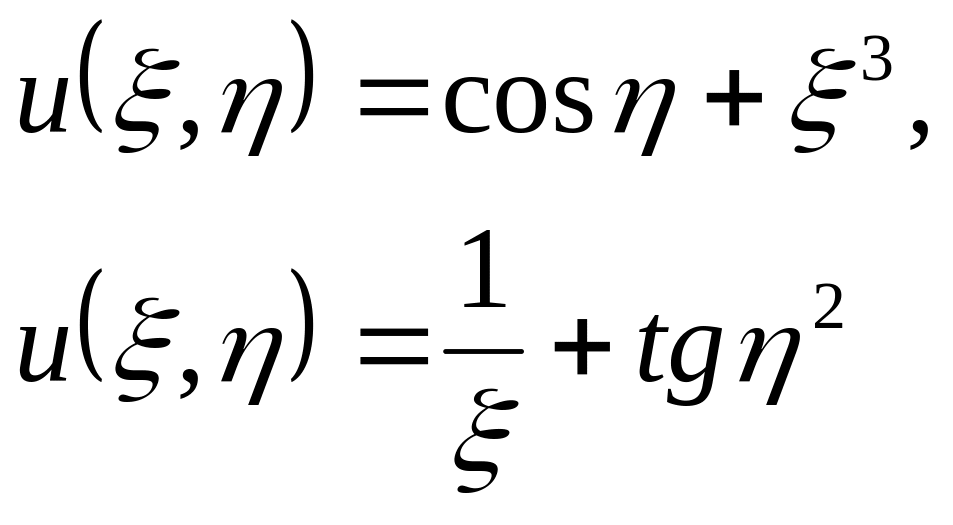
və s. funksiyaları (2.26) tənliyinin həlləridir.

(2.23) tənliyinin ümumi həllini tapmaq üçün (2.27)-də qəbul edirik və nəticədə

(2.28)

alırıq.

Fiziki olaraq dalğa tənliyinin ümumi həlli iki müxtəlif for­malı a sürəti ilə əks istiqamətlərdə yayılan dalğaların cəmi­dir (superpozisiyasıdır), f₁(x - at) sağa yayılan, f₂(x + at) sola yayılan dalğa adlanır.

(2.28) şəklində olan həllərdən (2.24) və (2.25) başlanğıc şərtlərini ödəyəni tapaq. Bu şərtlərdən

alınır.

İkinci bərabərliyi inteqrallasaq, və funksiyala­rı­nı tapmaq üçün aşağıdakı iki tənliyi alarıq:

(2.29)

burada x₀ – ixtiyari sabit ədəddir. (2.29)-dan

(2.30)

olduğunu tapırıq. (2.30) funksiyalarının ifadələrini (2.28) bəra­bər­liyində yerinə yazsaq, (2.23) – (2.24) Koşi məsələsinin həlli olan Dalamber düsturunu alırıq:

(2.32)

(2.23) – (2.24) məsələsinin yuxarıda göstərilən həllinin tapıl­ması üsuluna xarakteristikalar üsulu və ya yayılan dalğalar üsulu deyilir.

(2.32)-də birinci toplanan başlanğıc sürət sıfır olduqda ( ) başlanğıc yerdəyişmənin yayılma prosesini, ikinci toplanan isə başlanğıc yerdəyişmə sıfır ( ) olduqda rəqslərin başlanğıc sürəti (və ya impulsu) tərəfindən əmələ gəlməsi prosesini ifadə edir.

Məsələ 2.4. Yarımməhdud simin nöqtələrinin başlanğıc vəziyyəti və sürəti məlum olduqda onun rəqslərinin qanununu ifadə edən funksiyanı tapmalı.

Həlli. Məsələni həll etmək üçün

(2.33)

(2.34)

(2.35)

(2.36)

şərtlərini ödəyən u(x,t) funksiyasını tapmaq lazımdır.

(2.33) – (2.36) məsələsinin həlli üçün birbaşa Dalamber düsturundan istifadə etmək olmaz, belə ki, (2.32) düsturuna daxil olan x – at mənfi ola bilər və arqumentin mənfi qiymətləri üçün funksiyaları təyin olunmamışdır.

və funksiyalarının tək davamları olan və funksiyalarına baxaq:

Onda

(2.37)

funksiyası bütün x-lər və t >0-lar üçün təiyn olunmuşdur, bu funksiya sola və sağa yayılan dalğaların superpozisiyaları oldu­ğuna görə (2.33) dalğa tənliyini ödəyir. (2.37) funksiyasının (2.34) başlanğıc və (2.36) sərhəd şərtlərini ödədiyini yoxlayaq:

,

,

(2.37)-də x = 0 qəbul etsək,

alarıq. və tək funksiyalar olduğundan

,

deməli, u(0,t)=0.

Əvvəlki funksiyalara qayıtsaq, (2.33) – (2.36) məsələsinin həllini aşağıdakı kimi yazmaq olar:

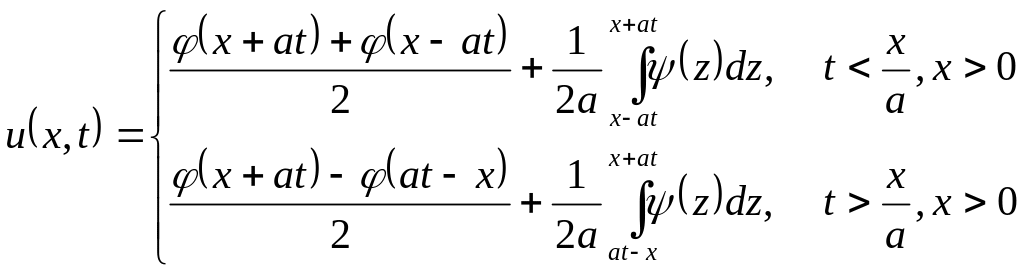(2.38)

Eyni qayda ilə, x=0 ucu sərbəst olarsa,

(2.39)

alarıq,

və funksiyalarının cüt davamları olan

funksiyalarını götürsək, rəqslər tənliyinin həllərini belə taparıq:

(2.40)

Bu funksiya oblastında (2.33) tənliyini, (2.34) – (2.35) başlanğıc şərtlərini və (2.39) sərhəd şərtini ödəyir.

Məsələ 2.5. Birölçülü dalğa tənliyi üçün sərhəd reji­mi­nin yayılması haqqında məsələni həll etməli.

Həlli. Yarımməhdud düz xətt üzərində birölçülü dalğa tənliyi üçün qeyri-bircins sərhəd məsələsinə baxaq:

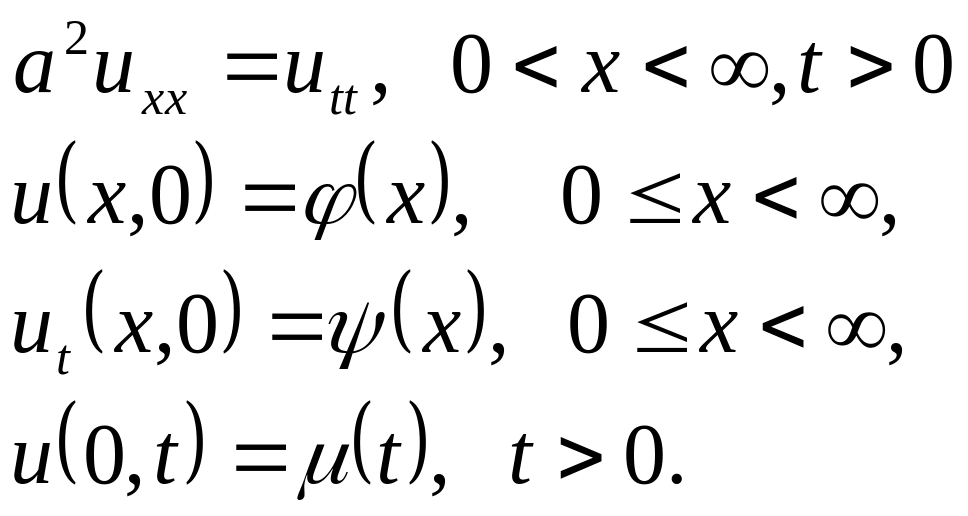(2.41)

(2.41) məsələsinin həllini

(2.42)

şəklində axtaraq, burada funksiyası

(2.43)

funksiyası isə

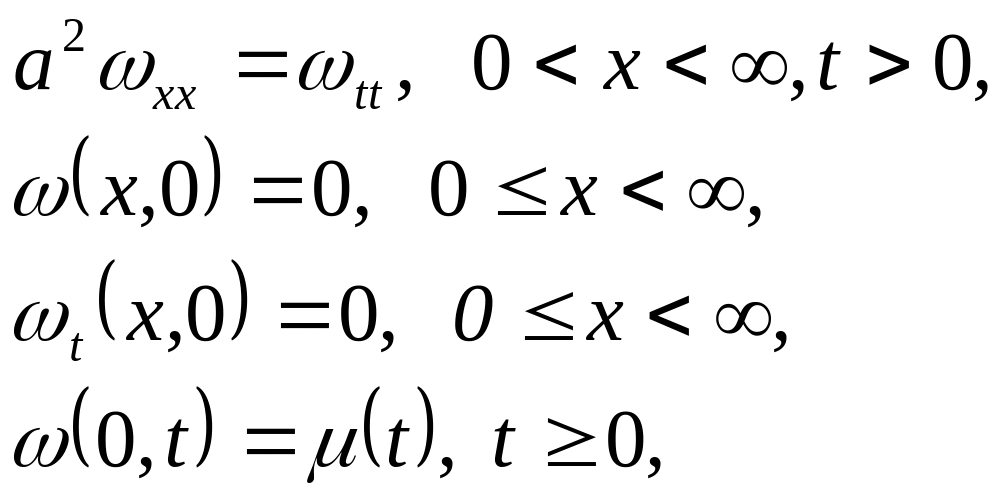(2.44)

sərhəd məsələlərinin həlləridir.

(2.43) məsələsini yuxarıda həll etmişik. Sərhəd rejiminin yayılması haqqında məsələ adlanan (2.44) məsələsini həll edək. Aşkardır ki, sərhəd rejimi sim boyunca sağa a sürəti ilə yayılan dalğa əmələ gətirəcək, bu isə həllin

analitik şəklində olmasını göstərir.

f funksiyasını

sərhəd şərtindən tapsaq,

,

buradan isə

olur. Deməli,

Eyni qayda ilə ikinci sərhəd məsələsinin həllini də qürmaq olar.

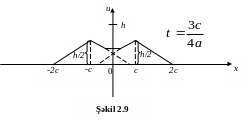
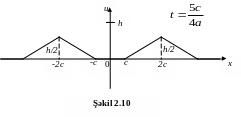
Məsələ 2.6. Qeyri-məhdud simin başlanğıc profili şəkil 2.6-dakı kimi verilmişdir. Zamanın

anlarında simin profilini çəkməli (başlanğıc sürət sıfra bəra­bərdir).

Həlli. Bu məsələdə olduğundan

olur. t=0 anında sağa və sola yayılan və dalğalar üst-üstə düşür. t >0 üçün sağa və sola ya­yı­lan dalğalar uyğun olaraq, sağa və sola qədər yerini də­yi­şə­cəkdir. Bütün anlar üçün yerdəyişmənin qrafiklərini top­la­maq­la simin t₁, t₂, … anları üçün profilini alarıq (şək.2.6-2.10).

Məsələ 2.7. Simin məcburi rəqslərinin tənliyi üçün Koşi məsələsini həll etməli.

Həlli. Məsələdə

(2.45)

(2.46)

(2.47)

şərtlərini ödəyən funksiyasını tapmaq tələb olunur. Məsələnin həlli

şəklində axtarılır. Burada

isə

(2.48)

(2.49)

şərtlərini ödəyən funksiyalardır. Dalamber düsturuna görə

olar. funksiyasını tapmaq üçün

şərtlərini ödəyən funksiyasını daxil edək və göstərək ki,

(2.50)

funksiyası (2.48) Koşi məsələsinin həllidir.

(2.50) funksiyası (2.48) tənliyini ödəyir, belə ki,

Deməli, .

(2.50) funksiyası (2.49) başlanğıc şərtlərini də ödəyir. Beləliklə, (2.48) – (2.49) məsələsinin həlli funksiyasının tapılmasına gətirilir.

funksiyası bircins tənliyi və -da uyğun başlanğıc şərtəlrini ödədiyindən, Dalamber düsturuna əsasən

olar. Onda

və

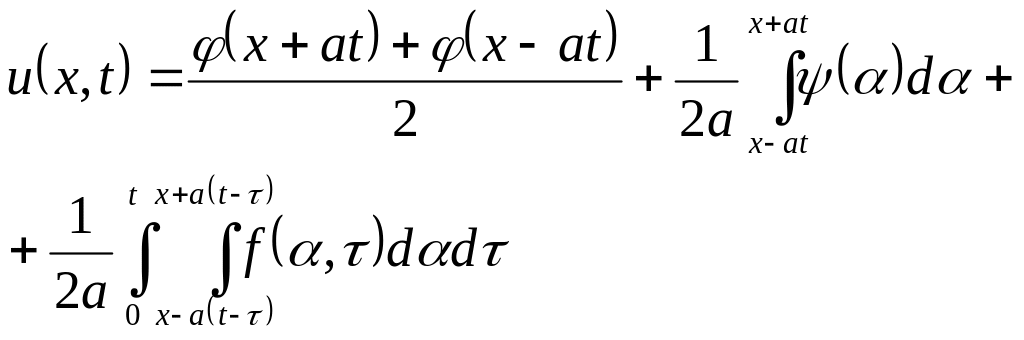
funksiyası (2.45) – (2.47) Koşi məsələsinin həlli olar.