Giriş

Riyazi fizika – fiziki proseslərin riyazi modellərini öyrənir və həm riyaziyyatda, həm də fizikada xüsusi yer tutur.

XIX əsrin ikinci yarısından başlayaraq, riyazi fizikanın üsul­ları müxtəlif təbiətli fiziki proseslərin öyrənilməsində mü­vəf­fəqiyyətlə tətbiq olunmağa başlanmışdır. Bu proseslərin ri­ya­zi modelləri əsasən xüsusi törəməli diferensial tənliklərlə ifa­də olunduğundan həmin tənliklərə riyazi fizika tənlikləri adı ve­rilmişdir.

Diferensial tənliklərdən başqa, fiziki proseslərin riyazi mo­del­lərini qurmaq üçün inteqral tənliklərdən, inteqro-dife­ren­sial tənliklərdən, bu modelləri tədqiq etmək üçün ehtimal və variasiya üsullarından, potensiallar nəzəriyyəsindən və başqa üsullardan istifadə olunur. Hesablama riyaziyyatının sürətli in­ki­şafı ilə əlaqədar olaraq, riyazi modellərin öyrənilməsində EHM-dən istifadə etməklə birbaşa ədədi üsulların (sonlu fərq­lər və s.) tətbiqi xüsusi əhəmiyyət kəsb edir. Bu üsulların kö­mə­yi ilə qaz dinamikasının, plazma fizikasının, süzülmə nəzə­riy­yəsinin və s. proseslərin bir çox yeni (düz və tərs) mə­sə­lələ­ri­ni həll etmək mümkün olmuşdur.

Təklif olunan dərs vəsaiti riyazi fizika tənlikləri fənninin müxtəlif bölmələrinə aid məsələlərin həllinə həsr olunmuşdur. Bu vəsaitin yazılması ilk növbədə azərbaycan dilində riyazi fizika tənliklərindən ədəbiyyatın azlığı və məsələ həllinə dair isə demək olar ki, vəsaitin olmaması ilə əlaqədardır. Əlbəttə, və­saitdə riyazi fizika tənlikləri fənninin bütün bölmələrini ge­niş əhatə edən məsələlərin həlli üsullarını göstərmək məqsədi qar­şıya qoyulmamışdır.

Əsas məqsəd – mümkün qədər kiçik həcmdə riyazi fizika tənlikləri fənninin əsas bölmələrinə aid nəzəri məlumatı vermək və tipik məsələlərin həll üsullarını göstərməkdir.

Hər bölmədə müstəqil həll etmək üçün məsələlər və onla­rın cavabları, bu məsələlərin həlli üçün zəruri olan göstərişlər və bəzi məsələlərin həlli verilmişdir.

Vəsait ilk növbədə «Kompüter elmləri» ixtisası üzrə təhsil alan tələbələr üçün nəzərdə tutulmuşdur. Lakin ondan texniki ali məktəblərin başqa ixtisasları üzrə təhsil alan tələbələr, magistraturaya hazırlaşan bakalavrlar, habelə riyazi fizika ilə müstəqil məşğul olmaq istəyənlər də istifadə edə bilərlər.

1. Xüsusi törəməli iki tərtibli diferensial tənliklərin təsnifatı və onların kanonik şəklə gətirilməsi

Asılı olmayan x₁, x₂,…,x_n dəyişənləri, məhcul u(x₁, x₂,…,x_n) funksiyası, onun 1-ci və 2-ci tərtib xüsusi törəmələri arasında olan

münasibətinə n sərbəst dəyişənli iki tərtibli xüsusi törəməli diferensial tənlik deyilir.

Əgər tənlik

(1.1)

şəklində olarsa, belə tənliyə yüksək tərtibdən törəmələrə nə­zə­rən xətti tənlik, F funksiyası da arqumet­lə­ri­nə nəzərən xəttidirsə, yəni (1.1) tənliyi

(1.2)

şəklində olarsa, ona xətti tənlik deyilir. burada a_ij, b_i və c əm­sal­ları yalnız x₁, x₂,…,x_n sərbəst dəyişənlərindən asılı funk­si­ya­lardır. Əgər əmsalları sərbəst dəyişənlərdən əlavə -dən asılı olarsa, (1.1) tənliyinə kvazixətti tənlik deyilir.

Əgər (1.2) tənliyində olarsa, ona bir­cins, əks halda qeyri-bircins xətti tənlik deyilir. (1.2) tənli­yin­də a_ij b_i, c əmsalları sabit olarsa, ona sabit əmsallı xətti tənlik deyilir.

Yüksək tərtibdən törəmələrə nəzərən xətti (və ya sadəcə xətti) tənlikləri üç tipə ayırmaq olar. Tənliyin bu və ya digər tipə aid olması məchul funksiyanın yüksək tərtibdən törəmələ­ri­nin əmsalları ilə təyin olunur.

Məchul u funksiyasının iki sərbəst dəyişəndən asılı olan halı üçün, yəni u=u(x,y) olduqda diferensial tənliklərin təsnifatını verək. Bu halda (1.1) tənliyini

(1.3)

(1.2) tənliyini isə

(1.4)

şəklində yazmaq olar, burada a_ij b_i, c – yalnız x və y-dən asılı funksiyalardır.

Əgər hər hansı D oblastının bütün nöqtələrində diskriminantı müsbətdirsə, (1.3) tənliyinə D oblastında hiperbolik (hiperbolik tipli), olarsa parabolik (parabolik tipli) və olarsa elliptik (elliptik tipli) tənlik deyilir.

Asılı olmayan dəyişənlərin müəyyən əvəzləməsindən istifadə etməklə, (1.3) və (1.4) tənliklərini daha sadə şəklə - kanonik şəklə gətirmək olar. (1.3) tənliyində tərs çevirməyə malik

(1.5)

əvəzləməsindən istifadə etsək, həmin tənliyin yeni və dəyişənlərində ifadəsi

(1.6)

şəklində olar, burada

(1.7)

funksiyası u funksiyasının 2-ci tərtib xüsusi törəmələrindən asılı deyildir.

Tənlik xətti olarsa, yəni

olarsa, (1.5) əvəzləməsindən sonra alınan (1.6) tənliyi də xətti olar:

, (1.8)

burada

(1.9)

yoxlamaq olar ki, münasibəti doğrudur. Bu isə onu göstərir ki, (1.5) əvəzləməsi tənliyin tipini dəyişmir. Hər bir tip tənlik üçün funksiyasının tapılma qaydasını və bu tənliyin kanonik şəklini göstərək.

1. Əgər (1.3) tənliyi D oblastında hiperbolik olarsa, D oblastında elə və funksiyaları vardır ki, (1.5) əvəzləməsinin köməyi ilə (1.3) tənliyi aşağıdakı kanonik şəklə gətirilir:

(1.10)

Bu halda və funksiyaları və əmsallarının sıfra bərabər olması şərtindən tapılır və

(1.11)

tənliklərinin , ümumi inteqrallarının sol tərəflərinə bərabərdir, burada

, (1.12)

olduğunu qəbul etsək,

.

(1.11) diferensial tənliklərinə (1.3) tənliyinin xarakteristik tənlikləri, onların inteqrallarına isə (1.3) tənliyinin xarakte­ris­ti­kaları deyilir.

Beləliklə, (1.10) tənliklərinin ümumi inteqralları iki müx­tə­lif əyrilər ailəsini müəyyən edir və olduğuna görə hər biri müxtəlif əyrilər ailəsindən götürülmüş iki əyri heç yerdə bir-birinə toxunmur.

Çox vaxt hiperbolik tip tənliklərin ikinci kanonik şəklindən istifadə edilir.

və ya

(1.13)

götürsək (burada və yeni dəyişənlərdir) olar və, (1.10) tənliyi

(1.14)

şəklinə düşər.

2. Parabolik tip tənliklər üçün olduğundan (1.10) tənlikləri üst-üstə düşür və

ümumi inteqralına malikdir. Bu halda

əvəzləməsində olaraq, ikinci tərtib kəsilməz xüsusi törəmələri olan, və ya

şərtini ödəyən ixtiyari funksiya götürülür.

Nəticədə parabolik tipli tənliyin

(1.15)

kanonik şəkli alınır.

3. Elliptik tipli tənlik üçün olduğundan (1.10) tənliklərinin sağ tərəfləri kompleks qoşma olur:

.

Bu halda xarakteristikalar da kompleks qoşma olacaq və

əvəzləməsinin köməyilə (1.3) tənliyi (1.10) şəklinə gətirilir.

Kompleks dəyişənlərdən azad olmaq üçün yeni

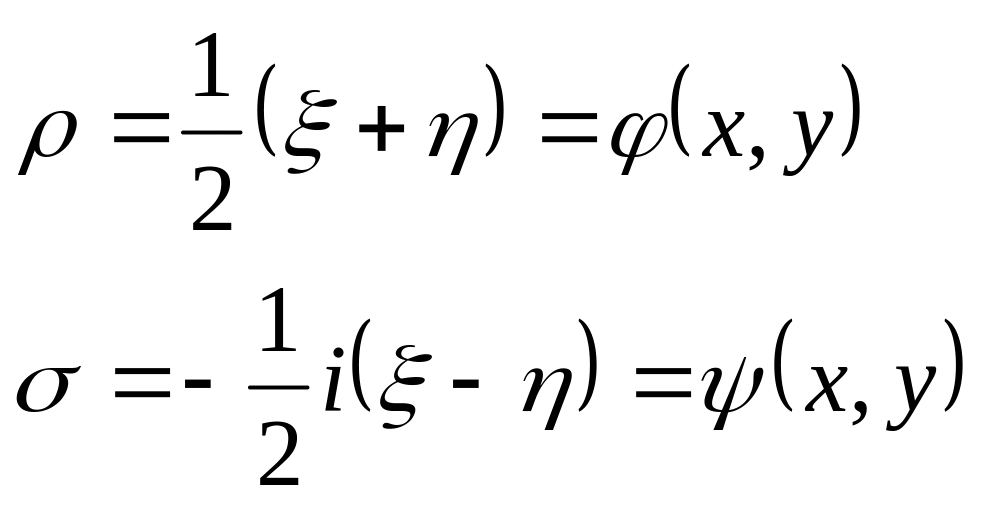
dəyişənlərini daxil etsək, (1.10) tənliyi və deməli, (1.3) tənliyi

(1.16)

kanonik şəklini alar.

Dəyişənlərin uyğun əvəzləməsi nəticəsində (1.4) xətti tənliyi aşağıdakı kanonik şəkillərin birinə gətirilir:

və ya (hiperbolik tip)

(parabolik tip)

(elliptik tip)

Tənliklərin kanonik şəkillərindən görünür ki, əgər (1.3) və (1.4) tənliklərində məchul funksiyanın qarışıq törəmələri iş­tirak etmirsə, onların tipini diskrimnantı hesablamadan müəy­yən etmək olar. Əgər və əmsallarının hər ikisi sıfırdan fərqli və müxtəlif işarəlı olarsa tənlik hiperbolik tipli, eyni işarəli olarsa elliptik tipli olur. Bu əmsallardan biri sıfırdan fərqli, digəri sıfra bərabər olarsa, tənlik parabolik tipli olur.

Göstərilən qaydanı (1.1) və (1.2) tənliklərinin tipinin təyin edilməsinə də tətbiq etmək olar. əgər verilmiş oblastın hər hansı nöqtəsində əmsallarının hamısı sıfırdan fərqli və eyni işarəli olarsa, (1.1) (və yaxud (1.2)) tənliyi bu nöqtədə elliptik, bu əmsalların hamısı sıfırdan fərqli, birindən başqa qalanları eyni işarəli olarsa, tənlik hiperbolik, əmsallarından biri sıfra bərabər, qalanları sıfırdan fərqli və eyni işarəli olarsa, tənlik parabolik olur. Məsələn,

tənliyi müstəvinin bütün nöqtələrində hiperbolik,

tənliyi parabolik,

tənliyi isə elliptikdir.

Misal 1.1. tənliyini kanonik şəklə gətirməli.

Həlli. Tənlik xəttidir və ,

olduğundan koordinat oxlarının nöqtələrindən başqa müstəvi­nin bütün nöqtələrində hiperbolik tiplidir.

Xarakteristikaların diferensial tənlikləri

,

onların ümumi inteqralları isə və olar.

və qəbul edərək, (1.8) tənliyinin əmsalları­nı (1.7) və (1.9) düsturlarının köməyilə hesablayaq (aşkardır ki, ):

Əmsalların alınan ifadələrini (1.8)-də yerinə yazsaq,

və ya

kanonik şəkildə tənliyi alarıq.

Misal 1.2. tənliyini kanonik şəklə gətirməli.

Həlli. Burada .

Deməli, oblastında tənlik hiperbolik tipli, oblastında isə elliptik tiplidir.

a) Əvvəlcə tənliyin hiperbolik tipli olduğu oblasta baxaq. Xarateristikaların diferensial tənlikləri

,

onların ümumi inteqralları isə

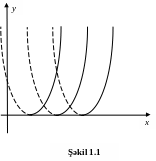
olar. Dəyişənlərin

əvəzləməsindən sonra verilmiş tənliyin

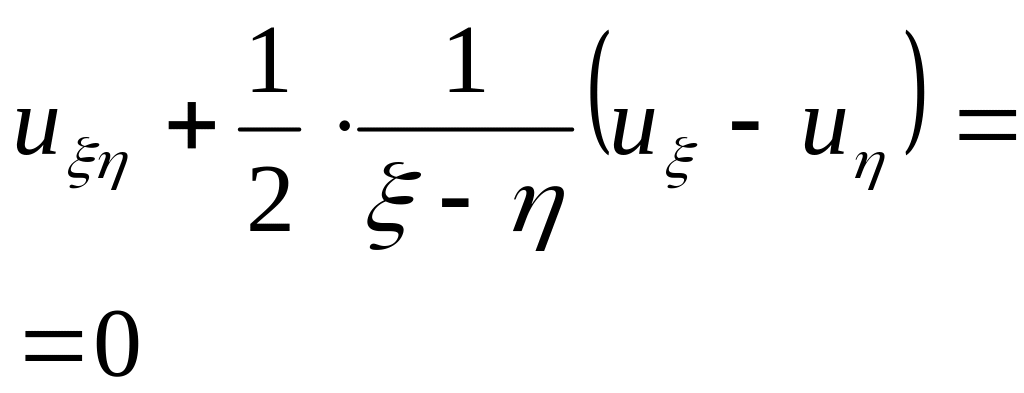kanonik şəklini alarıq.

Bu halda xarakte­ris­tikalar parabolalar ailə­sinin sağ və sol qol­ları olacaqdır (şəkil 1.1, bütöv və qırıq xət­lər). Parabolaların absis oxu üzərində yer­lə­şən təpələri xarak­teris­ti­kalara daxil deyil­dir, belə ki, bu ox üzərindəki nöqtələr tənli­yin hiperbolik olduğu oblastda deyil.

b) tənliyin elliptiklik oblastında dəyişən­lə­ri

şəklində əvəz etsək, sonuncu tənliyin yeni və dəyi­şən­lə­rində

kanonik şəklini alarıq.

Misal 1.3. tənliyini ka­no­nik şəklə gətirməli.

Həlli. Burada

.

Deməli, bu tənlik müstəvinin bütün nöqtələrində parabolik tiplidir. Onun

və ya

diferensial tənliyindən təyin olunan bir

xarakteristikalar ailəsi vardır. Buna görə də

qəbul edirik. Əgər, qəbul etsək,

olduğunu alarıq. Beləliklə

əvəzləməsinin köməyilə verilmiş tənlik

kanonik şəklinə gətirilir.

Misal 1.4. tənliyini qarışıq törəmə iştirak edən kanonik şəklə gətirin.

Həlli. Verilmiş hiperbolik tənlikdə

,

xarakteristik tənliklər

,

onların ümumi inteqralları

və

olar.

əvəzləməsini daxil edərək (1.7) və (1.9)-da alınan əmsalları (1.8)-də yerinə yazsaq, tənliyin

kanonik şəklini alarıq.

Misal 1.5. tənliyini qarışıq törə­mə iştirak etməyən kanonik şəklə gətirin.

Həlli. Misal 1.1-də bu tənliyi qarışıq törəmə iştirak edən

kanonik şəklə gətirmişdik. Yeni və ya əvəzləməsini daxil edərək, məchul funk­­si­yanın törəmələrinin yeni dəyişənlərlə (1.13) ifadələrini qarışıq törəmə iştirak edən tənlikdə yerinə yazsaq

və ya

kanonik şəkildə tənlik alınar.

Müstəqil həll etmək üçün məsələlər

Aşağıdakı tənliklərin hiperboliklik, paraboliklik, ellip­tik­lik oblastını tapmalı və hər bir oblastda onları kanonik şəklə gətirməli:

1.

Cavab: , ,

, ; ,

.

2.

Cavab: ,

x >0, y >0 və ya x < 0, y < 0;

,

x >0, y < 0 və ya x < 0, y > 0.

3.

Cavab: .

4.

Cavab: .

5.

Cavab: , y > 0;

, y < 0.

6.

Cavab: ,

, .

7.

Cavab: ,

.

8.

Cavab: .

9.

Cavab:

.

10.

Cavab: .

11.

Cavab:

.

12.

Cavab: .

13.

Cavab: .

14.

Cavab: .

15.

Cavab: .

16.

Cavab: .

17.

Cavab: .

18.

Cavab: .

19.

Cavab: .

20.

Cavab: .

21.

Cavab: .

22.

Cavab: .

23.

Cavab: .

24. tənliyinin ümumi həllini tapın.

Cavab: .

Göstəriş: Tənliyi kanonik şəklə gətirin, alınan tənliyin ümumi həllini tapın və bu həllin ilkin dəyişənlərdə ifadəsini yazın.

25. tənliyinin ümumi həllini tapın.

Cavab: .