
- •4.2. Основні елементи кінематики рівномірного обертального руху
- •5. Закон Гука. Діаграма напружень.
- •6. Обертовий рух. Основний закон динаміки обертового руху. Теорема Штейнера.
- •7.Механічний принцип відносності і перетворення Галілея.
- •8. Елементи ств Енштейна. Перетворення Лоренца і наслідки що з нього випливають.
- •5.Фаза коливань.
- •Перетворення енергії при гармонічних коливаннях
- •18. Основне рівняння мкт ідеального газу
- •17/////4.6. Внутрішня енергія і теплоємність ідеального газу
- •Розподіл частинок у потенціальному силовому полі
- •Перше начало термодинаміки
- •21. Оборотні процеси. Цикли. Теплові двигуни і холодильні машини. Друге начало термодинаміки.
- •33. Робота і потужність у колі постійного струму. Закон Джоуля-Ленца
- •34. Розгалужені кола. Правила Кірхгофа.
- •35. Електричний струм в металах, газах та рідинах.
- •36. Магнітне поле та його характеристики.
- •41 Самоіндукція і взаємоіндукція. Індуктивність.
- •42 Енергія магнітного поля.
- •§ 2. Інтерференція світла в тонких плівках
- •49 Дифракція світла
- •Дифракція на щілині[
- •55. Закони випромінювання абсолютно чорного тіла Закон випромінювання Планка
- •Три закони фотоефекту:
- •58. Ефект Комптона
- •61.Співвідношення невизначеностей Гейзенберга
- •62.Хвильова функція і її статистичний зміст
- •63.Рівняння Шредінгера
- •64. Постулати Бору
- •69. Реакції поділу та синтезу ядер.
- •70. Природна радіоактивність ядер. Закон радіоактивного розпаду.
8. Елементи ств Енштейна. Перетворення Лоренца і наслідки що з нього випливають.
В 1905 році у роботі „До електродинаміки рухомих середовищ” А.Ейнштейн показав, що закони класичної механіки і перетворення Галілея вірні, лише коли ми маємо справу з невеликими швидкостями руху тіл і вважаємо, що швидкість розповсюдження взаємодії між тілами безконечно велика.
При швидкостях близьких до швидкості світла необхідно користуватись більш загальними законами релятивістської механіки. Основою релятивістської механіки є два постулати Ейнштейна:
1. Принцип відносності - в довільній інерціальній системі всі фізичні явища при їх тотожній постановці протікають однаково. Всі закони природи і рівняння, що їх описують, інваріантні при переході від однієї інерціальної системи відліку до іншої.
Інакше кажучи: ніякими експериментами неможна визначити, чи знаходиться дана інерціальна система в спокої, чи рухається рівномірно і прямолінійно.
2. Принцип постійності швидкості світла - швидкість світла в вакуумі є величиною постійною і однаковою в усіх інерціальних системах відліку, вона не залежить від швидкості руху джерела світла чи спостерігача.
Перетворення Лоренца
Існування
верхньої границі для швидкості світла
(![]() у
вакуумі) привело до отримання Лоренцом
формул, що зв’язують події в рухомій і
нерухомій системах відліку при швидкостях
близьких до
у
вакуумі) привело до отримання Лоренцом
формул, що зв’язують події в рухомій і
нерухомій системах відліку при швидкостях
близьких до ![]() .
.
І.
Нехай рухома інерціальна система
рухається
відносно нерухомої
з
швидкістю ![]() так,
що осі
так,
що осі ![]() і
і ![]() співпадають.
співпадають.

Рис. 2
Координати і час для точки відносно рухомої системи записуються:
![]()
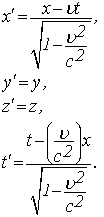
Така система рівнянь називається прямим перетворенням Лоренца (знаходження координат і часу події, що відбулась відносно рухомої системи відліку).
Зауваження. При ![]() дані
рівняння переходять в рівняння Галілея.
дані
рівняння переходять в рівняння Галілея.
ІІ. Запишемо тепер обернені перетворення Лоренца (знаходження координат і часу події відносно нерухомої системи відліку).
![]()

Висновки з перетворень Лоренца:
1. Швидкість ![]() системи
чи тіла не може бути рівна швидкості
світла у вакуумі (
системи
чи тіла не може бути рівна швидкості
світла у вакуумі (![]() ),
бо тоді підкореневий вираз перетворюється
в
),
бо тоді підкореневий вираз перетворюється
в ![]() ,
а значить
,
а значить ![]() ∞,
∞, ![]() ∞,
що немає фізичного змісту .
∞,
що немає фізичного змісту .
2. При ![]() підкореневий
вираз стає від’ємний і перетворення
втрачають математичний зміст.
підкореневий
вираз стає від’ємний і перетворення
втрачають математичний зміст.
10.Гармонічними коливаннями називаються періодичні коливання фізичної величини (або будь-якої іншої) залежно від часу, які відбуваються згідно із законами синуса або косинуса
![]() ,
,
або
![]() ,
,
де ![]() —
це фізична величина, що коливається,
—
це фізична величина, що коливається, ![]() —
час,
—
час, ![]() —
це найбільше значення, яке приймає
величина
—
це найбільше значення, яке приймає
величина ![]() під
час коливань, яке
називають амплітудою коливань,
під
час коливань, яке
називають амплітудою коливань, ![]() — циклічна
частота коливань,
— циклічна
частота коливань, ![]() — фаза коливань.
— фаза коливань.
Періодом коливань називається величина
![]() .
.
Лінійна частота коливань визначається, як
![]() .
.
В результаті дії різноманітних сил, які призводять до втрати енергії, коливання можуть згасати. В такому випадку вони описуються формулою
![]() .
.
Величина ![]() називається декрементом
згасання коливань.
Обернена до декременту величина
називається сталою
часу згасаючих
коливань.
називається декрементом
згасання коливань.
Обернена до декременту величина
називається сталою
часу згасаючих
коливань.
Гармонічні коливання дуже розповсюджені в природі й техніці. До них належать малі коливання підвішеного на пружині тягаря, малі коливання маятника, коливання в молекулах, якими зумовлене поглинання інфрачервоних променів, різноманітні коливання в електротехніці, наприклад у коливальному контурі та інші.
Амплітудою гармонічних коливань називається модуль найбільшого значення коливної величини ( Іm, Um, Qm ).
Це може бути модуль електричного заряду або будь-якої інщої величини, що періодично змінюється. Амплітуда може мати різні значення, в залежності від того, якого заряду було надано конденсатору в початковий момент часу. Інакше кажучи, амплітуда визначається початковими умовами.
Період і частота коливань.
Під час коливань значення заряду конденсатора періодично повторюється. Мінімальний проміжок часу Т, через який процес повторюється повністю, називається періодом коливань.
Період вільних коливань тягарця на пружині визначали за формулою
 .
.
|
Скориставшись аналогією між механічними і електромагнітними коливаннями. Дістанемо формулу для періоду вільних коливань у контурі:
![]() .
.
|
Ця формула називається формулою Томсона – на честь англійського фізика, котрий вперше її вивів.
Знаючи період, можна визначити частоту коливань, тобто кількість коливань за одиницю часу:
 .
.
Циклічна частота ( кількість коливань за 2П секунд) визначається як
 .
.
